物理のエッセンスの電磁気編コンデンサーの問題 38* について解説します。
電子の導体中での運動からオームの法則を導きます。
最初、問題を見て、???となった人も多いかもしれません。
入試ではあるレベル以上では必ず、見たことがない問題が出ます。
同じ問題を出していては本当の実力を測るのが難しいと考えるのでしょうか?
そんなとき、基本原則に立ちかえって根本から考えるのが解けるようになる秘訣です。
電磁気38*の問題解説
物理のエッセンスの電磁気編 P70 の 38* の問題を参照してください。
動画解説
テキスト解説

問題概要:平均自由行程から導体の抵抗についての考察を得ます。
運動方程式から古典的な考察を行い、電気抵抗と、導体断面積・導体長さとの関係を得ます。
このグラフで示されているような考え方には一度は慣れておきましょう。
まず抵抗の考え方ですが、電子が運動して金属の陽イオンに衝突することにより生じると考えます。
これは渋谷の交差点を全力で駆け抜ける行為に似ています。
走っても、すぐに人にぶつかって減速するでしょう。ひどいときは転んでしまうかもしれません。
でもすぐ立ち上がって走り出すということを繰り返します。
導体中の電子も、金属陽イオンに衝突して減速しても、すぐにめげずに加速するのです。
その時の平均の速さを $v$ としています。
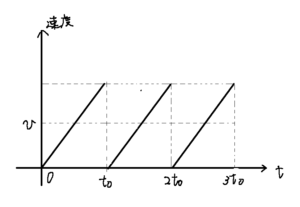
このグラフを見ると、時間 $t_0$ の間隔で加速減速を繰り返しています。
したがって、最大速度を $v_{max}$ とでもすると、$v_{max}=2v$ と書けます。
また、運動方程式より、
$ma=F$
です。そして、電場から電子が受ける力は、$F=eE$ です。
ここで、導体長さが $l$ ですから、電池電圧を $V$ とすると、$E=\dfrac{V}{l}$ です。
したがって、
$ma=F=eE=e\dfrac{V}{l}$
より、
$a=\dfrac{eV}{ml}$
となります。
ここで、電子は初速度 0 、加速度 $a$ の等加速度運動をすると考えられるので、
$v_{max}=at_0=\dfrac{eV}{ml}t_0$
です。$v_{max}=2v$ だったので、これを代入して、
$v=\dfrac{eVt_0}{2ml}$
となります。
さて、ここで有名な式($e$ 電気素量、$n$ 電子密度、$v$ 電子の速さ、$S$ 導体断面積 です)
$I=envS$ (ワタシ I はブスネー vSne と覚える。 または、ワタシ I はエンガチョブス envS )
より、
$\begin{split}
I&=envS\\\\
&=en\dfrac{eVt_0}{2ml}S\\\\
&=\dfrac{e^2nSt_0}{2ml}V
\end{split}$
これと、オームの法則 $I=\dfrac{1}{R}V$ とを比較します。
そうすると、
$R=\dfrac{2m}{e^2nt_0}\dfrac{l}{S}$
となりますね。
したがって、
$R=\rho \dfrac{l}{S}$
が得られます。ここで $\rho=\dfrac{2m}{e^2nt_0}$ です。
さて、いかがでしたでしょうか?
目新しい問題も、落ち着いて根本に帰って考えれば突破口が開けます。
では!







































コメント