虚光源と組み合わせレンズ
虚光源とは、1枚目のレンズでできた像が、作図上2枚目のレンズの後方に位置する場合です。
1枚目のレンズを出た光は、虚光源にあつまるように2枚目のレンズに入射します。
エッセンスの問題で虚光源を解説しています。
まずは、一般的な組み合わせレンズから解説します。
組み合わせレンズ
2枚のレンズを組み合わせた場合について考えます。
焦点距離はそれぞれ $f_1$、$f_2$
基本的には、
- 物体から出る光を考えて、1枚目のレンズで生じる像を考えます。
- 1枚目のレンズで出来た像を、新しい物体として2枚目のレンズでできる像を考える。
という手順で行います。
まず簡単な例から行きましょう。
1枚目のレンズによる像が虚像のとき
図を見てください。
2種類のレンズをおいて、そのときに観測される像を考えます。
まず1枚目のレンズによる像を考えます。
この例ではレンズ前方に虚像が観測されます。
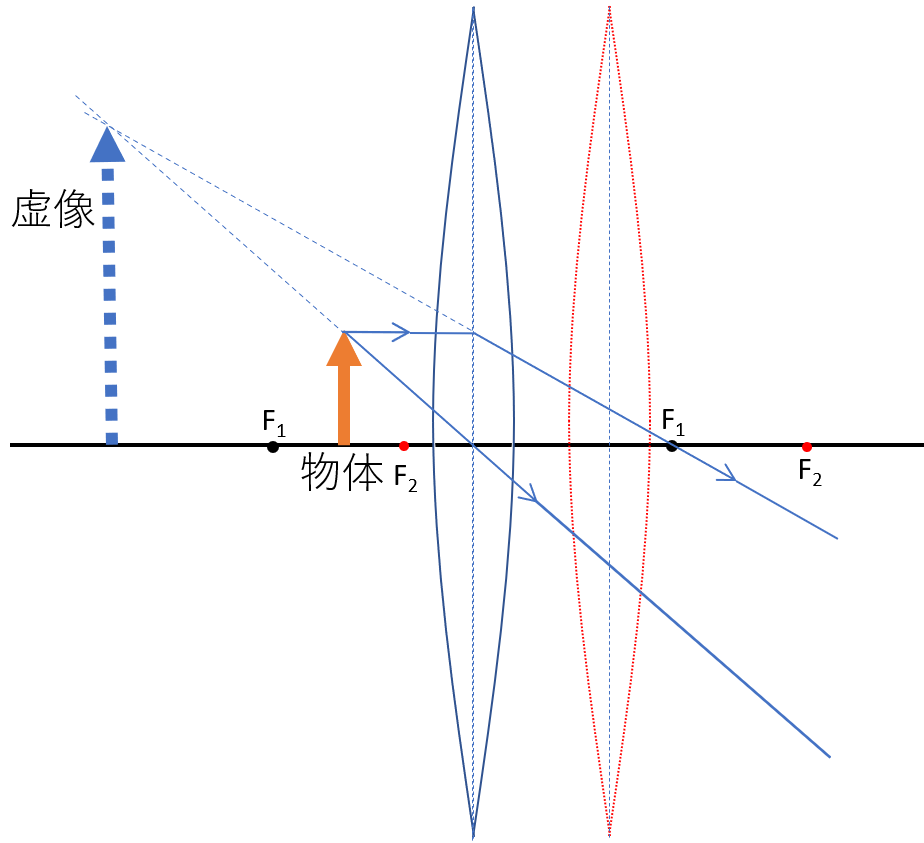
そのうえで、虚像を光源として、2枚目のレンズによる像を考えます。
まとめると次のような図になります。
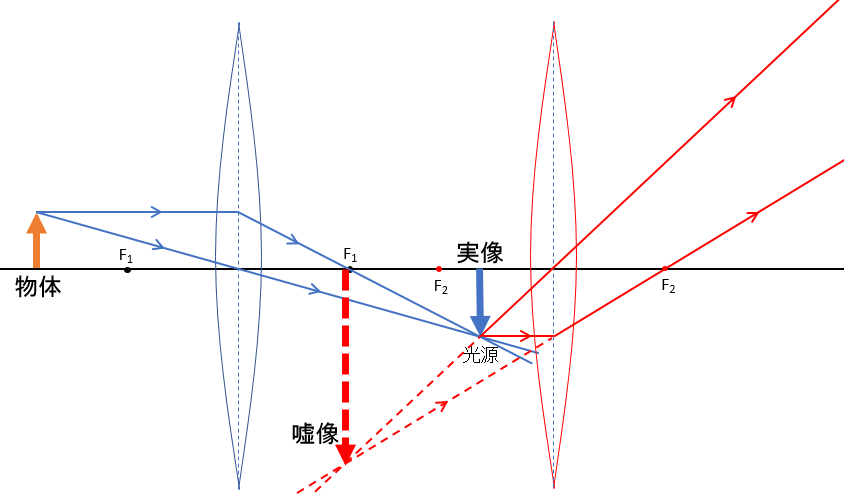
1枚目のレンズによる像が実像のとき
では、1枚目のレンズでレンズ後方に実像ができるときはどうするか？
これには、できる実像が、2枚目のレンズの前方にできるか、後方にできるかで変わってきます。
まず、2枚のレンズの間に、1枚目のレンズによる実像ができるときは、その実像を新たな光源として考えればよいだけです。
凸レンズ－凸レンズ
１．一枚目のレンズによる像が2枚目のレンズの焦点の外側にある場合
２．一枚目のレンズによる像が2枚目のレンズの焦点の内側にある場合
望遠鏡や顕微鏡はこのような虚像を観察しています。
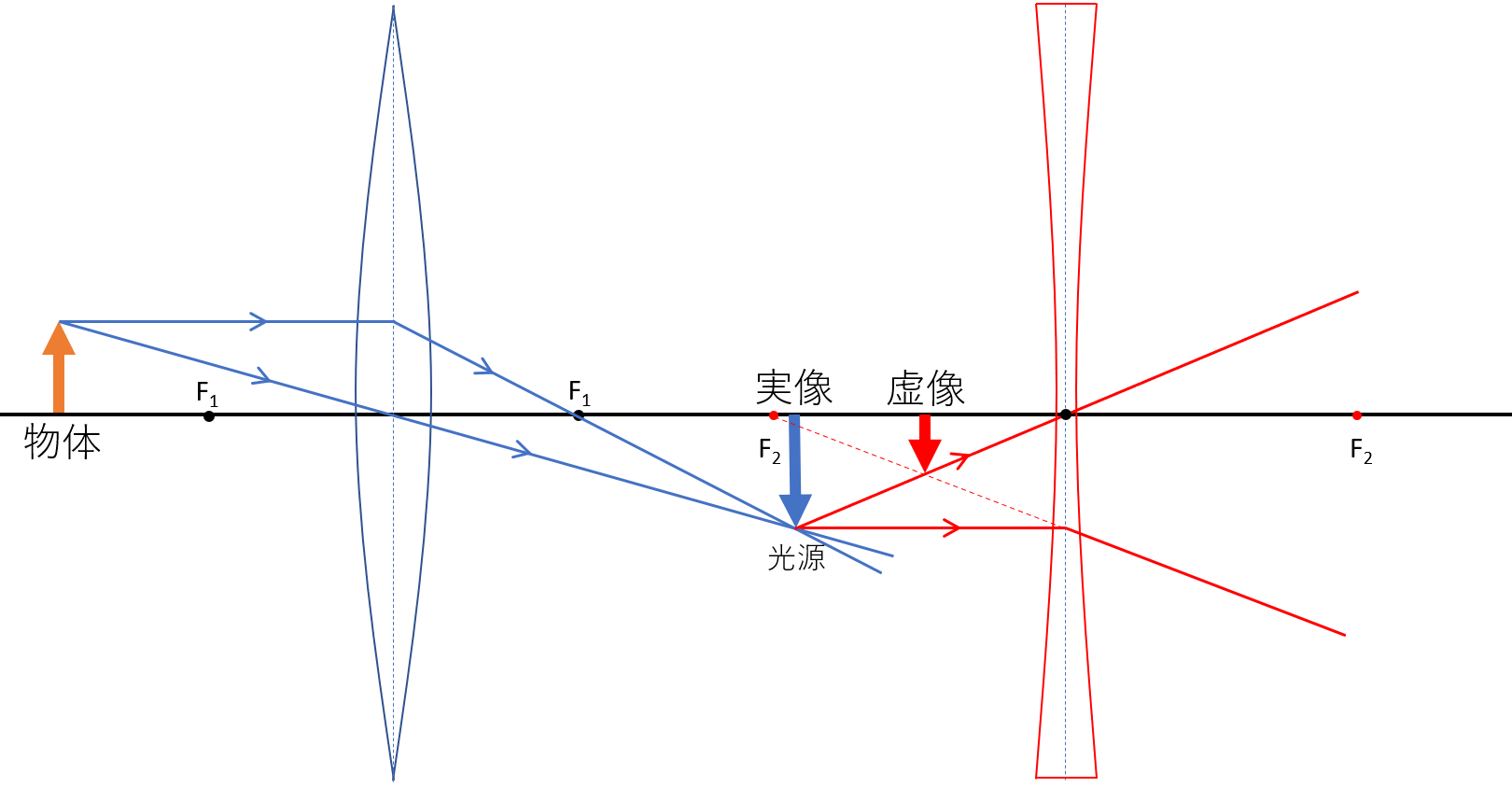
凸レンズー凹レンズ
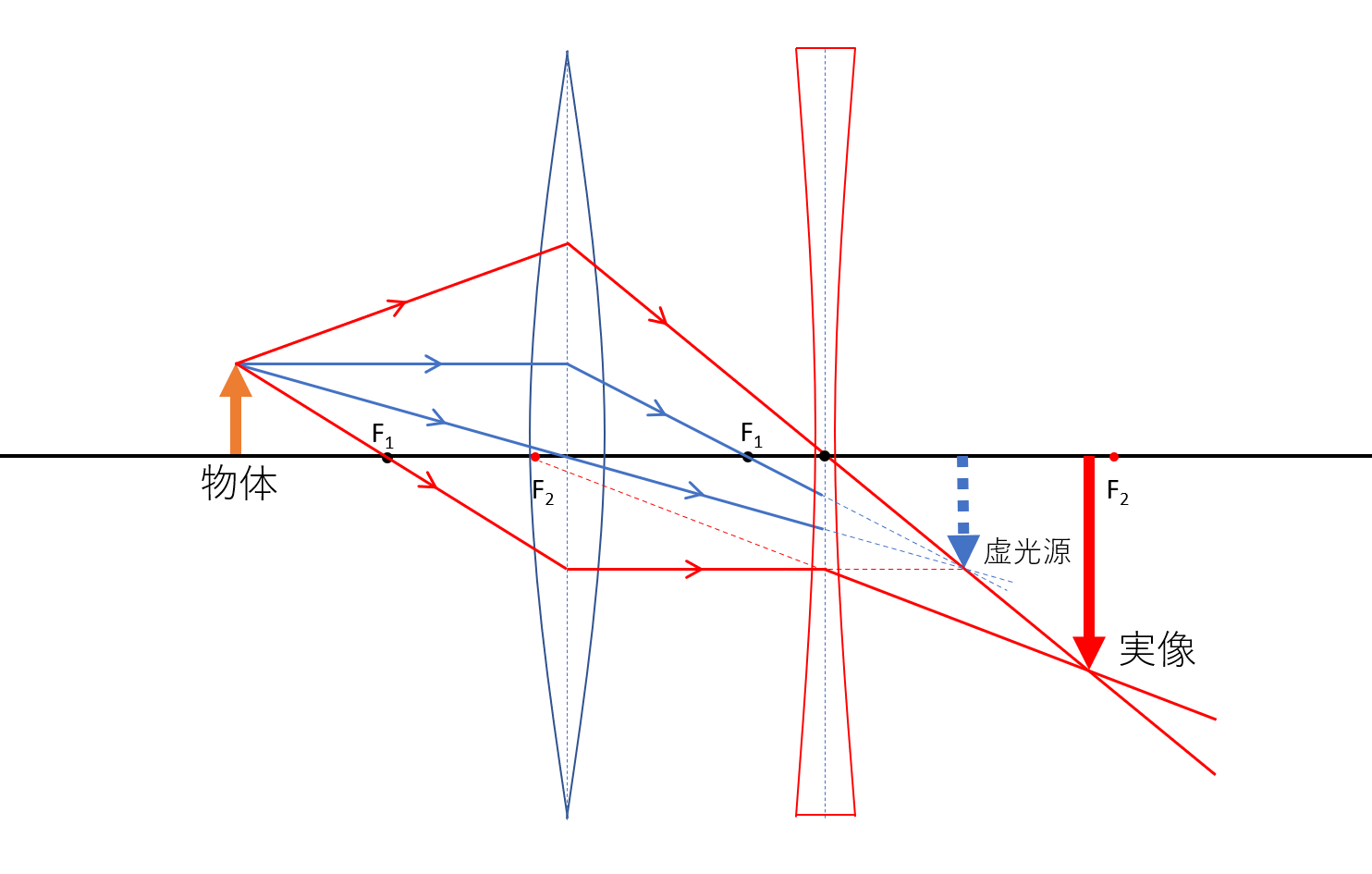
虚光源
2枚目のレンズが凸レンズ
問題は1枚目のレンズによる実像が、2枚目のレンズの後方にできる場合です。
（といっても、2枚目のレンズがあるため、実際にはこの実像はできません）
このとき、仮の実像ができるところを考え、この光の集まるところを虚光源といいます。
そして、1枚目のレンズを通った光はすべて、虚光源に向かいます。
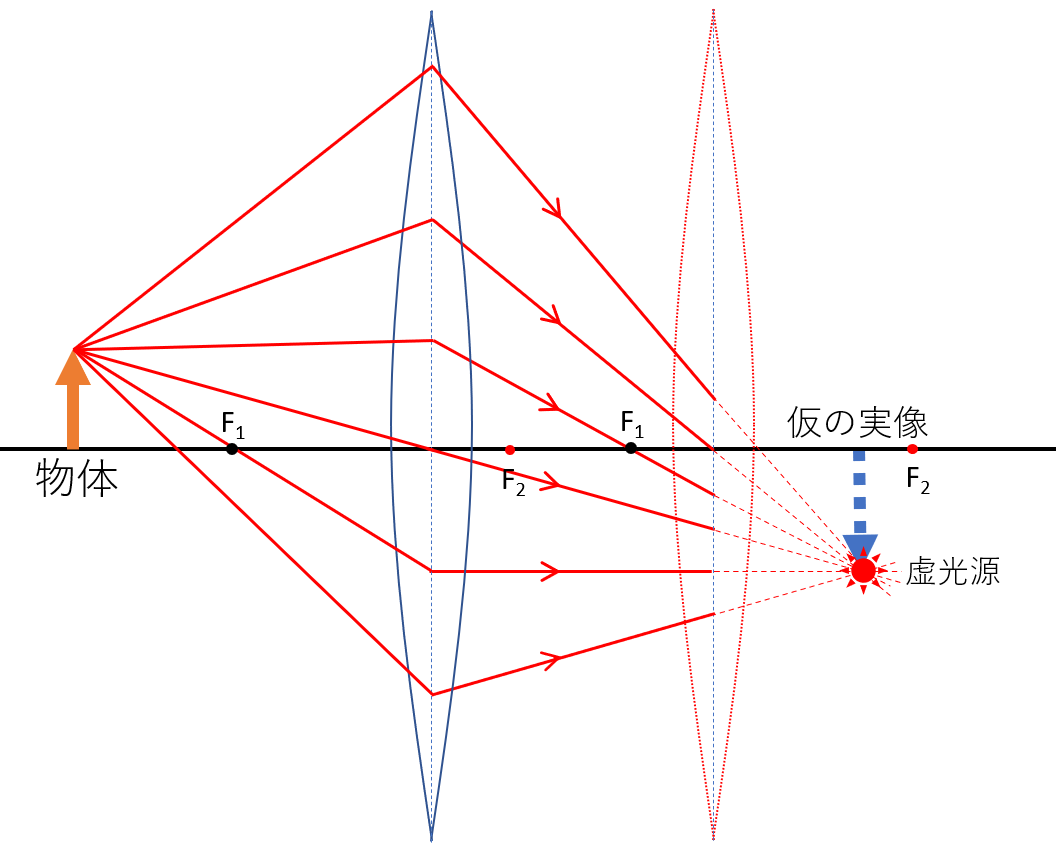
像を作図するには、図のように虚光源に向かう、描きやすい光路を考えてみましょう。
具体的には、2枚目のレンズ中心を通る光と、光軸に平行な光です。
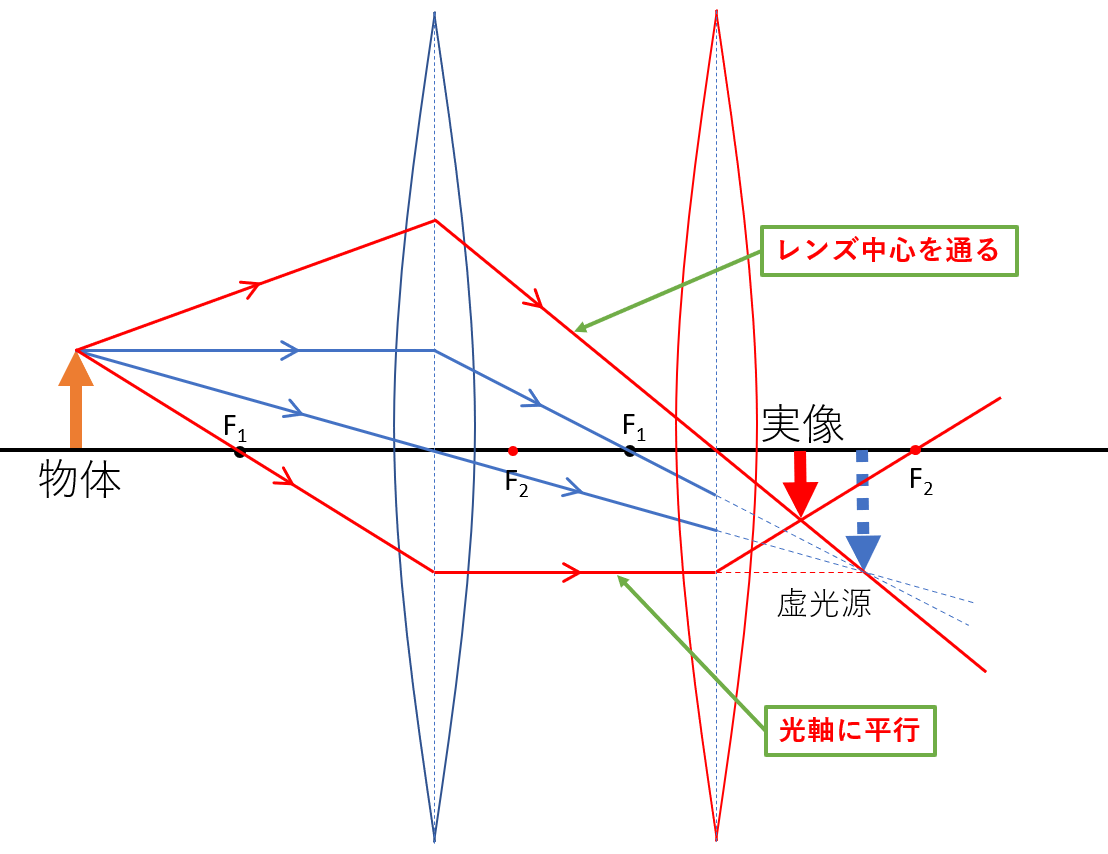
そうすると、これらの光が2枚目のレンズで屈折して交わるところに、像が作図できます。
この場合は、実像ができました。
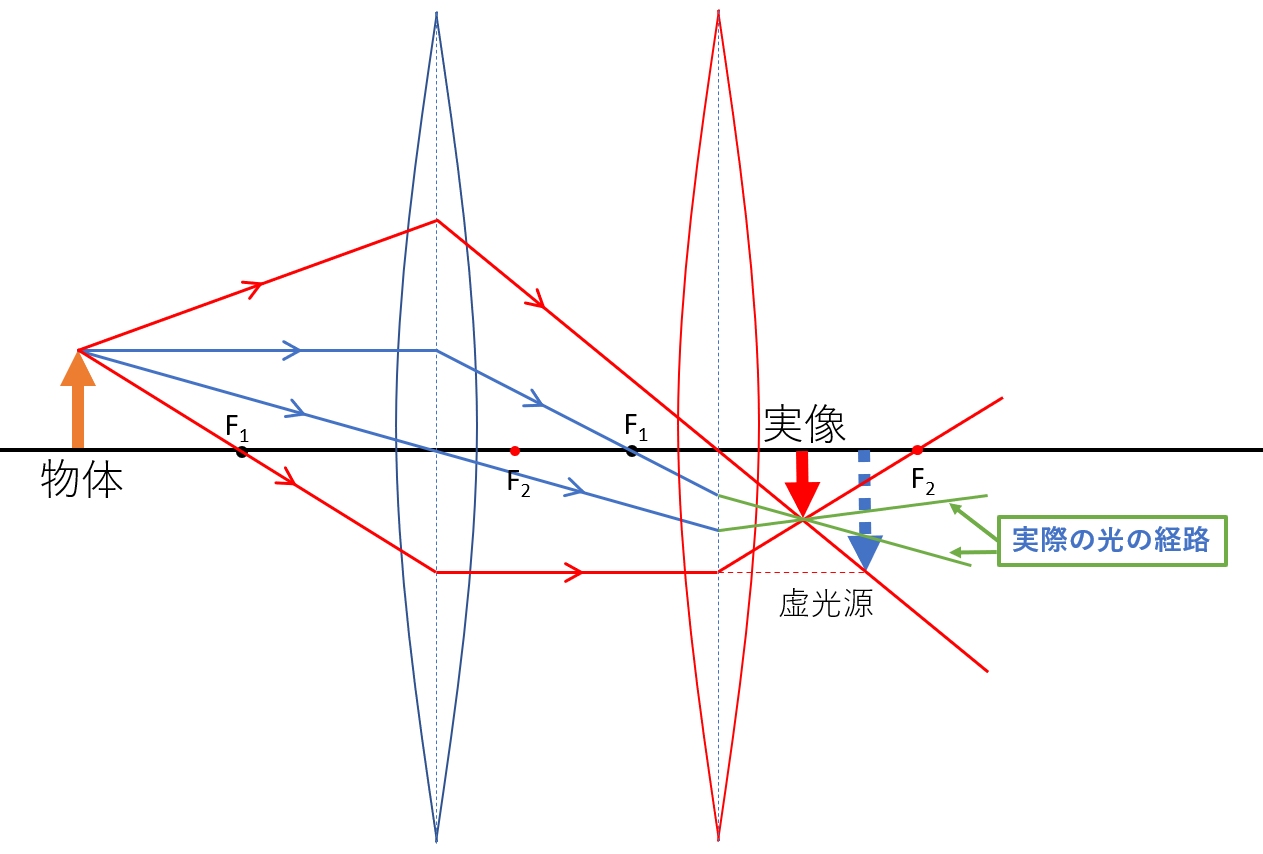
そして先ほどの図で青の点線で描いた、虚光源へ集まる光は、実際には次の図の緑の線のように屈折します。
2枚目のレンズが凹レンズ
同じく、2枚目のレンズが凹レンズの場合も虚光源（青の点線の集光するところ）を考えます。
そして、描きやすい光、2枚目のレンズ中心を通る光と、光軸に平行な光を考えます。
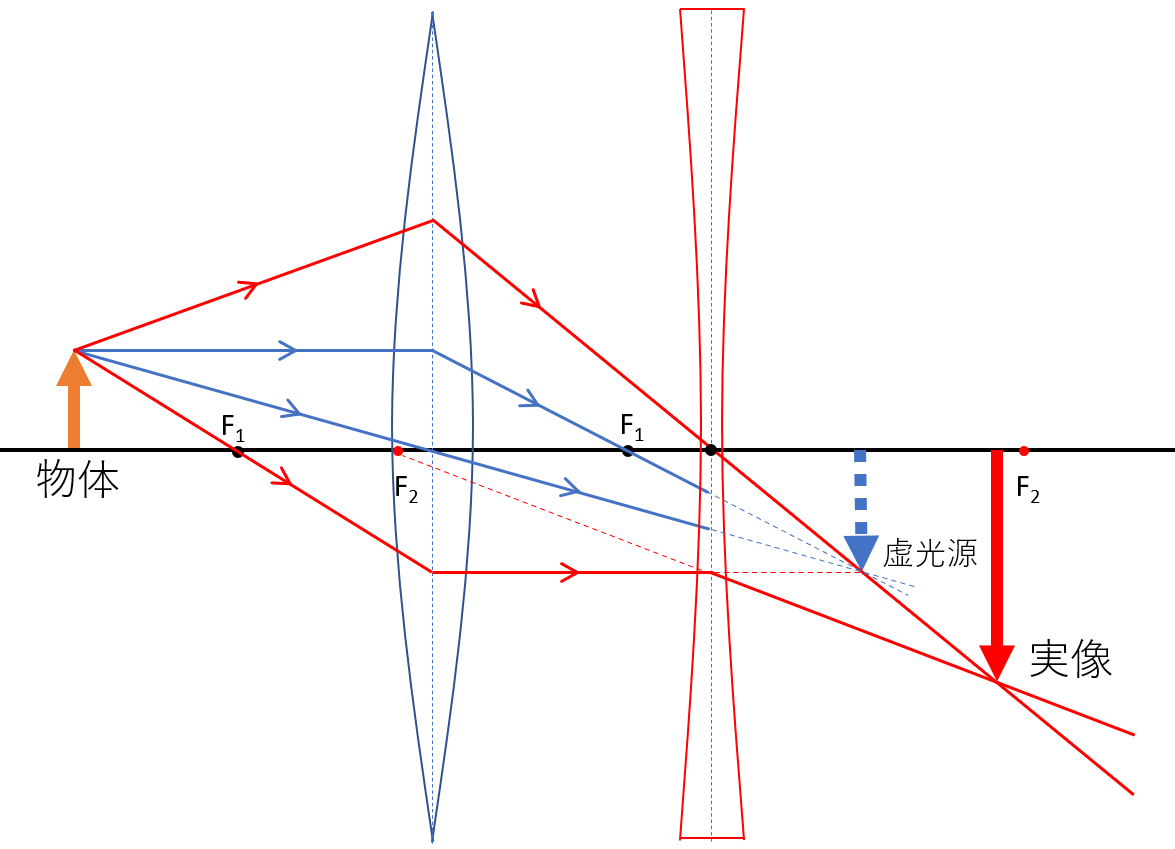
2枚目のレンズを通った、青の点線で示された光の、実際の経路を緑で示します。
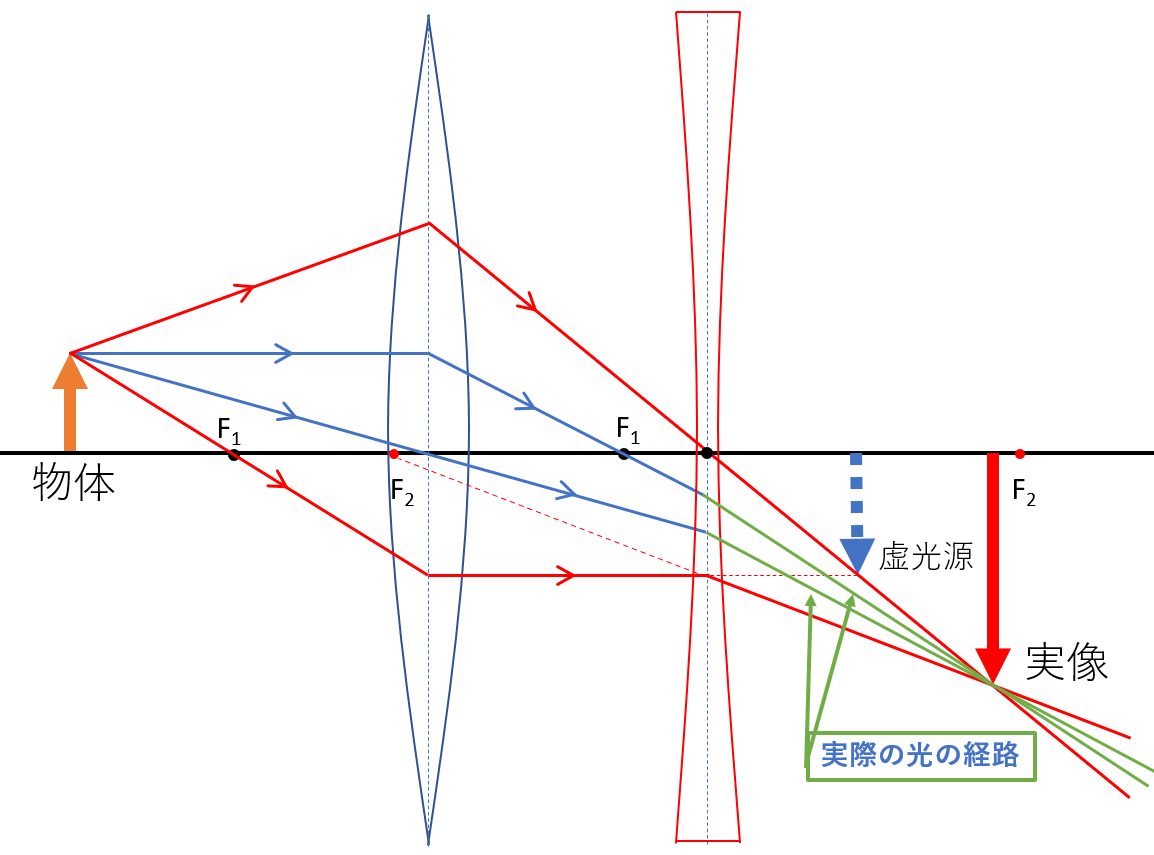
この場合（虚光源が凹レンズとその焦点距離の間にある場合）は、凹レンズにより、拡大された実像ができました。
写像公式
よく知られている、
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$
の式において、$a$ はレンズと物体の距離、$b$ はレンズと像の距離、$f$ は焦点距離です。
一般に、次の表のように考えればよいでしょう。虚光源の時は $a<0$ となります。
倍率は、 $\left|\dfrac{b}{a}\right|$ です。
レンズが2枚の場合は、それぞれのレンズについて写像公式を適用します。
写像公式については、いずれまた詳しく解説する予定です。
コメント