 いまさら聞けない
いまさら聞けない いまさら聞けない スリット間隔
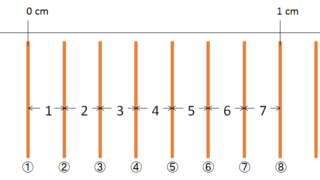
いまさら聞けない スリット間隔の疑問 スリットの本数が1 cmあたり8本のとき、スリット間隔はいくらになるのか? 図解してみました。
 いまさら聞けない
いまさら聞けない  いまさら聞けない
いまさら聞けない  波動
波動  波動
波動 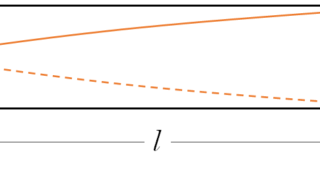 波動
波動  波動
波動  波動
波動 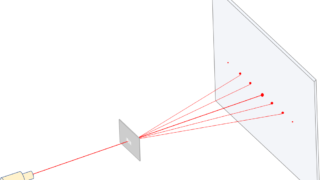 波動
波動 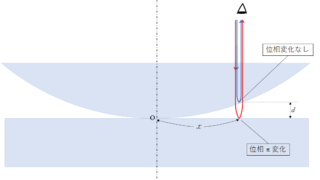 波動
波動 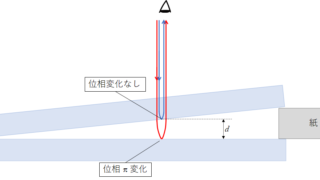 波動
波動  波動
波動  波動
波動  波動
波動  波動
波動  波動
波動  波動
波動  波動
波動  波動
波動  波動
波動  波動
波動