弦の振動

弦の振動

両端を固定した弦（ギターなどをイメージ）に生じる定常波について考えます。

定常波が生じるのは、左右から全く同じ波がやってくる場合です。
この場合、振幅も同じである必要があります。　こちらを参照　定常波と波の式

弦の両端は固定端となっていると考えられますから、（こちらも参照 ざるそばの波動 ）

弦をはじいた場合、その波動は左右両端で反射され戻ってきて、弦に定常波が生じると考えられます。

弦を伝わる波の速さ

弦を伝わる波の速さ $v$ は次の式で示されることがわかっています。

$v=\sqrt{\dfrac{S}{\rho}}$

$\rho$：線密度（単位長さ当たりの線の質量）

$S$：張力

この式の導出は次回以降で。

ギターの弦でも低音弦は太く、高音弦は細いですね。
また、弦を強く張れば張るほど高音になっていきます。

基本振動

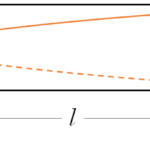
もっとも基本的な定常波です。

このとき、弦長を $l$ とすると、この定常波の波長 $\lambda $ は　$\lambda  = 2l$　です。
　　下図は短縮して描いてあります。

振動数を $f_1$ 、波の速さを $v$ とすると　$v=\sqrt{\dfrac{S}{\rho}}$　より、

$f_1 = \dfrac{v}{\lambda}=\dfrac{1}{2l}\sqrt{\dfrac{S}{\rho}}$

2倍振動

両端が節であることに注意して、基本振動の次の振動状態を考えます。

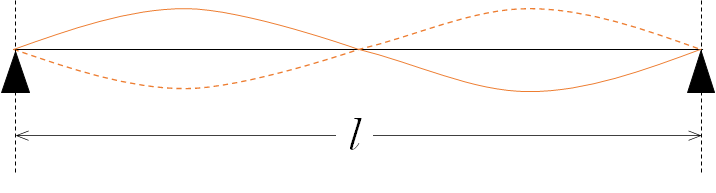
この場合、振動している波の波長 $\lambda $ は、以下の図から　$\lambda  = l$　です。

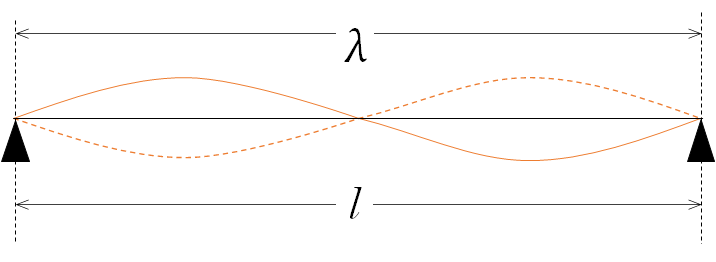
したがって、振動数 $f_2$ は、

$f_2 = \dfrac{v}{\lambda } = \dfrac{1}{l}\sqrt{\dfrac{S}{\rho}}$

これは、 $f_1 = \dfrac{1}{2l}\sqrt{\dfrac{S}{\rho}}$　から、

$f_2  =2 \times \dfrac{1}{2l}\sqrt{\dfrac{S}{\rho}} = 2f_1$

です。

3倍振動

2倍振動の次に考えられるのが次の図のような振動状態です。

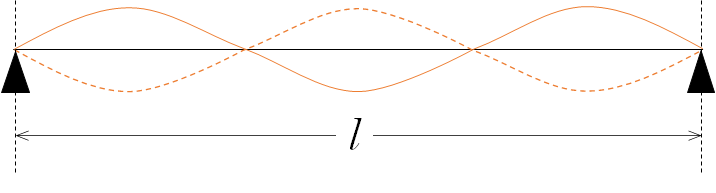
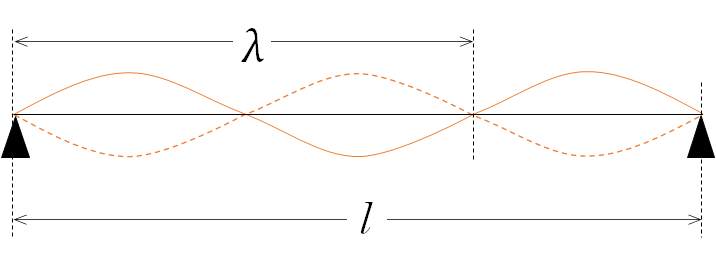
これが3倍振動なのですが、波長 $\lambda$ は、以下の図より

$\lambda  = \dfrac{2}{3}l$

です。

したがって、振動数 $f_3$ は、

$f_3 = \dfrac{v}{\lambda } = \dfrac{3}{2l}\sqrt{\dfrac{S}{\rho}}$

これは、 $f_1 = \dfrac{1}{2l}\sqrt{\dfrac{S}{\rho}}$　から、

$f_3 = 3\times \dfrac{1}{2l}\sqrt{\dfrac{S}{\rho}}= 3f_1$

です。