電位法によるコンデンサー回路の解法
コンデンサー回路は結構計算量が多く、ややこしくなることも多いのですが、電位法を用いれば短時間で、すっきりと解けたりします。(記事 : コンデンサーを含む回路もどうぞ)
やり方は
- 回路中にアースを仮定して電位の基準(0 V)とする。
- 孤立部位の電位を $x$ と仮定する。
- 各コンデンサーの電位を考え、たくわえられる電気量($Q=CV$)を計算する。
- コンデンサーの孤立部分で電気量保存則を適用して立式する。
- $x$ について式を解く
です。
他の解法も交えて、実際に問題を解きながら解説していきます。
最初は?となるかもしれませんが慣れれば強力なツールとなります。

ただし、基本的な考え方はオーソドックスな解法にあります。
その他の解法もしっかり理解しておくことが重要です。
練習問題
コンデンサーの接続
電気量がそれぞれ $2.0\:\mathrm{\mu F}$、$6.0\:\mathrm{\mu F}$ のコンデンサー $C_1$、$C_2$ および、電圧 $8.0 \:\mathrm{V}$ の電池、そしてスイッチ $S_1$、$S_2$ を使って図の回路を作った。最初スイッチ $S_1$、$S_2$ はともに開いている。
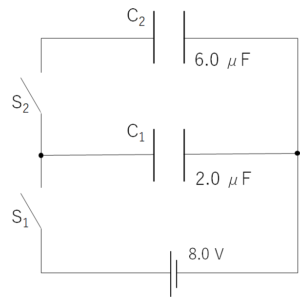
スイッチ $S_1$ を閉じ、十分時間が経過した後、$S_1$ を開き、その後、$S_2$ を閉じた。
$C_1$ と $C_2$ に蓄えられている電気量を求めよ。
すべての解法で以下のことは共通です。
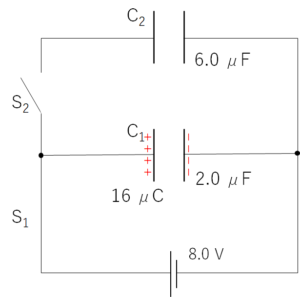
- $S_1$ を閉じた後、最初に $C_1$ に電荷 $Q_1$ がたまります。
$Q=CV$ より、$Q_1=C_1V=2.0 \times 8 =16 \:\mathrm{\mu C} $
- $S_1$ を開き、$S_2$ を閉じたあと、コンデンサーにかかる電圧は共通です(並列のため)。
これを $V^{\prime}$ とします。 -

- 最後の $C_1$ の電気量 $Q^{\prime}_1$ 、 $C_2$ の電気量 $Q^{\prime}_2 $ とします。
解法1 電位法
一度 $S_1$ を閉じた後、同じく $S_1$ を開くため、それ以降、電池は無関係になります。
そして $S_2$ を閉じると、$C_1$ にあった電荷が移動します。
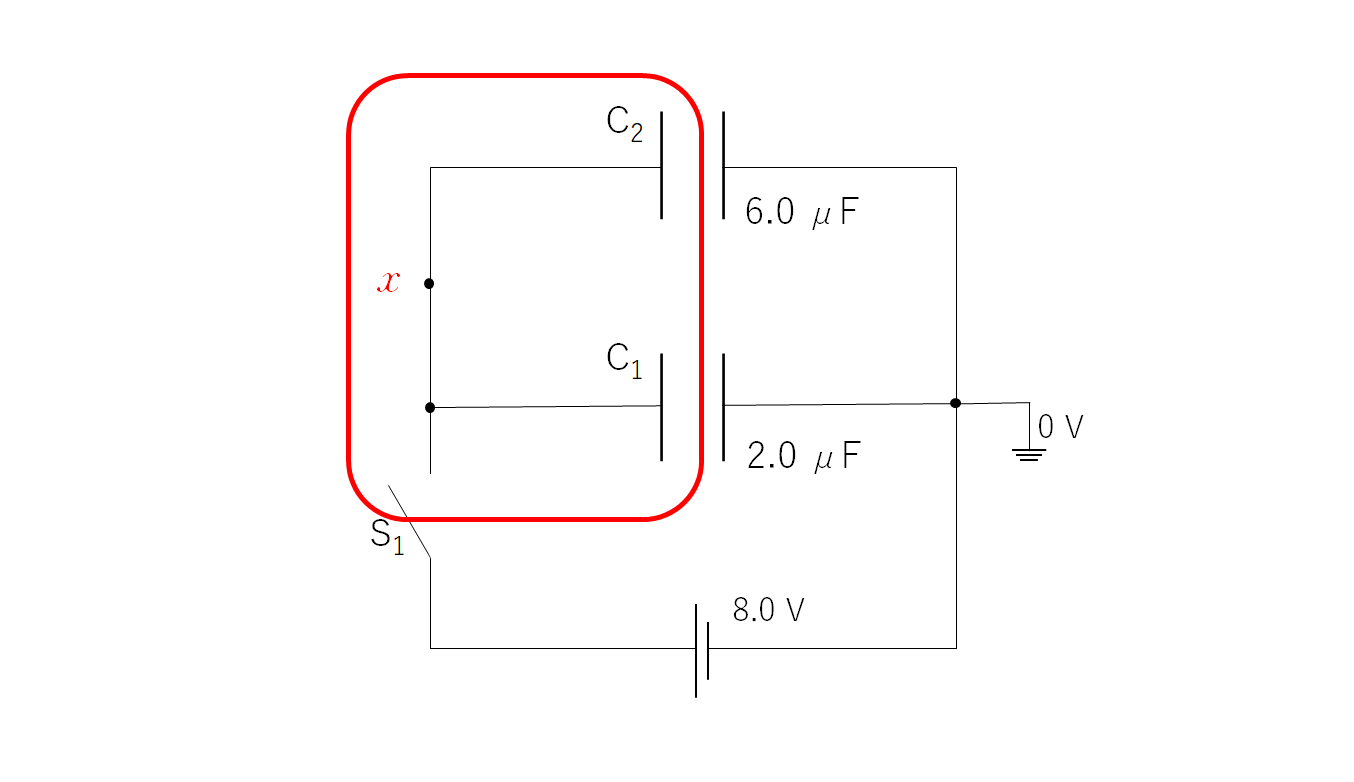
回路中の適当なところにアースを仮定します。
このアースは電位基準を考えるためで、回路に影響を及ぼしません。

要は $Q=CV$ の式における電位差 $V$ を考えるためのものです。
だから $0\:\mathrm{V}$ でなくても構いません。0 とするのは簡単のためです。
ここで図の点の電位を $x$ とします。
このとき、赤で囲まれた部分は孤立しているため、電荷総量は一定です。
このことを利用して式をたてていきます。

コンデンサーの電荷量計算は次のようにしてください。
コンデンサーの電気量計算を次のようにします。
$Q=CV$ において $V$ は極板間の電位差です。
そこで コンデンサー極板にたまる電荷の正負も含めて、次のように示すことができます。$Q = C(V_{\mathrm{自分}} – V_{\mathrm{相手}})$
このようにすると、コンデンサーの極板上の電荷をその正負も含めて計算できるのです。
例
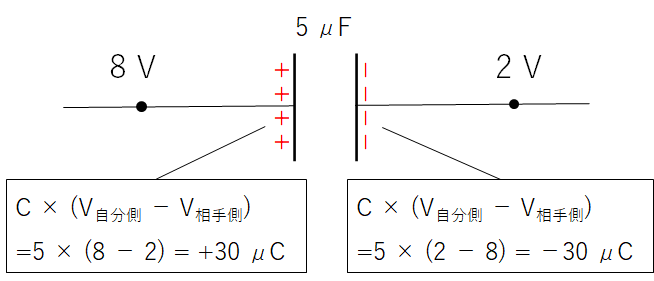
図ではコンデンサーの電気容量 $C=5 \:\mathrm{\mu F}$ 電位を $8\:\mathrm{V}$ 、 $2\:\mathrm{V}$ としています。
そうすると、図のコンデンサーの左側の極板にたまる電荷は
$Q_{\mathrm{左側}} = C(V_{\mathrm{自分}} – V_{\mathrm{相手}})=5 \times (8-2)=+30 \:\mathrm{\mu C}$
$Q_{\mathrm{右側}} = C(V_{\mathrm{自分}} – V_{\mathrm{相手}})=5 \times (2-8)=-30 \:\mathrm{\mu C}$
となり、極板にたまる電荷をその正負まで合わせて計算できていることがわかります。
同じように考えて

図の $C_1$ の左側の極板にたまる電気量は
$Q^{\prime}_{1\mathrm{左側}} = C(V_{\mathrm{自分}} – V_{\mathrm{相手}})=2 \times (x-0)=2x \:\mathrm{\mu C}$
$C_2$ の左側の極板にたまる電気量は
$Q^{\prime}_{2\mathrm{左側}} = C(V_{\mathrm{自分}} – V_{\mathrm{相手}})=6 \times (x-0)=6x \:\mathrm{\mu C}$
赤で囲った中の電気量の総量は $Q_1=C_1V=2.0 \times 8 =16 \:\mathrm{\mu C} $ でしたから、
$Q_1=16 \:\mathrm{\mu C} =Q^{\prime}_{1\mathrm{左側}} + Q^{\prime}_{2\mathrm{左側}} $
$16 \:\mathrm{\mu C} =2x + 6x =8x $
これより、
$x=2.0\:\mathrm{V}$
よって、
$Q^{\prime}_{1\mathrm{左側}} = C(V_{\mathrm{自分}} – V_{\mathrm{相手}})=2 \times (2-0)=4.0 \:\mathrm{\mu C}$
$C_2$ の左側の極板にたまる電気量は
$Q^{\prime}_{2\mathrm{左側}} = C(V_{\mathrm{自分}} – V_{\mathrm{相手}})=6 \times (2-0)=12 \:\mathrm{\mu C}$
と計算できます。

特筆すべきは、もっともっとややこしい問題などでそれこそあっ!という間に解けたりすることです。
この問題は電位法を使うまでもない簡単なものですが、もっと複雑な回路でも考え方は同じです。
ここで理解できれば、応用が利くはずです。
あとでもっと難しい問題をやってみましょう!

その他の解法を次にいくつか紹介します。
解法2 並列利用
その1
$S_1$ を閉じた後開き、 $S_2$ を閉じれば、コンデンサーの $C_1$ と $C_2$ は並列です。
したがって、コンデンサーの合成容量 $C$ は、 $C=C_1+C_2=2.0 + 6.0 = 8.0 \:\mathrm{\mu F}$ です。
図の赤で囲まれた部分では、並列になっても電荷総量は $Q_1 = 16 \:\mathrm{\mu C}$ で変化しません。

ここで、 $Q=CV$ より、
$Q_1= CV^{\prime} $
$16 = 8.0 \times V^{\prime}$
$V^{\prime}=\dfrac{16}{8.0} =2.0\:\mathrm{V}$
よって
$C_1$ の電気量 $Q^{\prime}_1 = C_1V^{\prime} = 2.0 \times 2.0 = 4.0 \:\mathrm{\mu C}$
$C_2$ の電気量 $Q^{\prime}_2 = C_2V^{\prime} = 6.0 \times 2.0 =12 \:\mathrm{\mu C} $
その2
その1と同じことなのですが、比を使ってやってみましょう。
$S_1$ を閉じた後開き、 $S_2$ を閉じるとき、コンデンサーの $C_1$ と $C_2$ は並列です。
したがって、両コンデンサーにかかる電圧は同じです。
ここで、$Q=CV$ より、
$C_1$ の電気量 $Q^{\prime}_1$ 、 $C_2$ の電気量 $Q^{\prime}_2 $ の比を考えて、
$Q^{\prime}_1:Q^{\prime}_2 = C_1V^{\prime} : C_2V^{\prime} = C_1 : C_2 =2.0 : 6.0 = 1 : 3 $
図の赤で囲まれた部分では、並列になっても電荷総量は変化せず $Q_1 = 16 \:\mathrm{\mu C}$ です。

したがって、$Q^{\prime}_1$ と $Q^{\prime}_2$ の和は
$Q^{\prime}_1 + Q^{\prime}_2 =Q_1 = 16 \:\mathrm{\mu C}$
です。
これらより、
$Q^{\prime}_1 = \dfrac{1}{1+3}\times 16= 4.0 \:\mathrm{\mu C}$
$Q^{\prime}_2 = \dfrac{3}{1+3}\times 16= 12 \:\mathrm{\mu C}$
と計算できます。
解法3 オーソドックス
しつこいですが、オーソドックスな解き方でもやってみましょう。(結局、中身は変わりませんが)
図の赤で囲まれた部分では、並列になっても電荷総量は変化せず $Q_1 = 16 \:\mathrm{\mu C}$ です。

したがって、$Q^{\prime}_1$ と $Q^{\prime}_2$ の和は
$Q^{\prime}_1 + Q^{\prime}_2 =Q_1 = 16 \:\mathrm{\mu C}$
両コンデンサーは並列で電圧は $V^{\prime}$ です。
したがって、 $Q=CV$ より
$Q^{\prime}_1 = C_1V^{\prime} = 2.0 \times V^{\prime}$
$Q^{\prime}_2 = C_2V^{\prime} = 6.0 \times V^{\prime}$
これらを $Q^{\prime}_1 + Q^{\prime}_2 =Q_1 = 16 \:\mathrm{\mu C}$ へ代入して、
$2.0 \times V^{\prime} + 6.0 \times V^{\prime} = 16 \:\mathrm{\mu C}$
$V^{\prime} = \dfrac{16}{8.0} = 2.0 \:\mathrm{V}$
したがって、
$Q^{\prime}_1 = C_1V^{\prime} = 2.0 \times 2.0 = 4.0 \: \mathrm{\mu C}$
$Q^{\prime}_2 = C_2V^{\prime} = 6.0 \times 2.0 = 12 \: \mathrm{\mu C}$
注意:この問題に関しては、オーソドックスな方法は結果的には電位法とほぼ同じですが、考え方の違いを理解してください。




































コメント