事前に充電されたコンデンサーを2つ用意します。
そしてそれぞれのコンデンサーを + 極同士、-極同士つなぎます。
あるいはその逆、+と-極同士をそれぞれつなげた場合、これらはコンデンサーとして直列か並列かどちらなのでしょうか?
答えはどちらも並列となります。
さて、なぜかを考えましょう。
コンデンサーの並列・直列の基本についてはこちらへ
コンデンサーを充電する
コンデンサー を $3 \:\mu F$ と $2\:\mu F$ の2つ考えます。
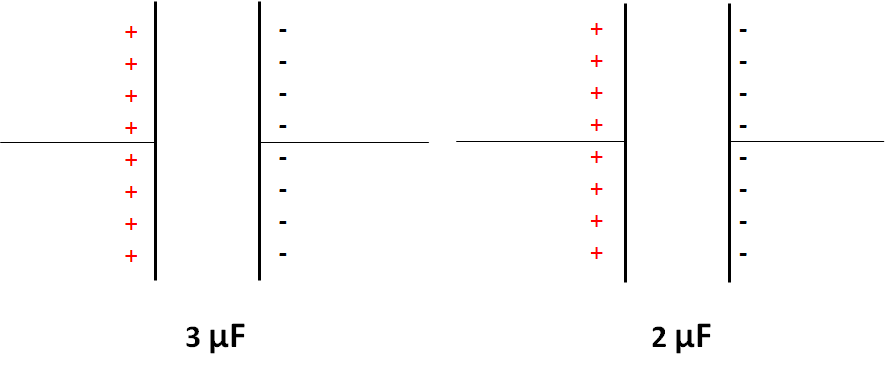
さて、これらをそれぞれ $10\:V$ と $20\:V$ で充電します。
そうすると、$Q=CV$ より、
$Q=3\:\mu F \times 10\:V =30\:\mu C$
$Q=2\:\mu F \times 20\:V =40\:\mu C$
の電気量がたまります。
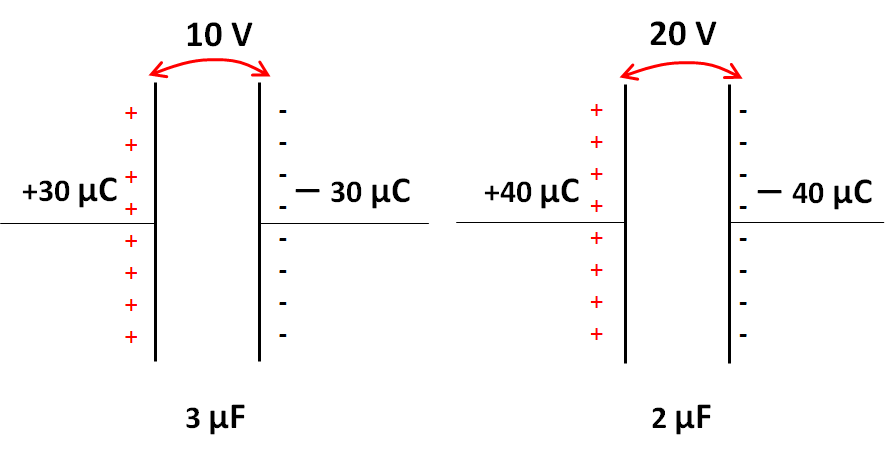
コンデンサーの接続 1
そして次の図のように接続しましょう。
まずは、 + 極同士、-極同士でつなげます。
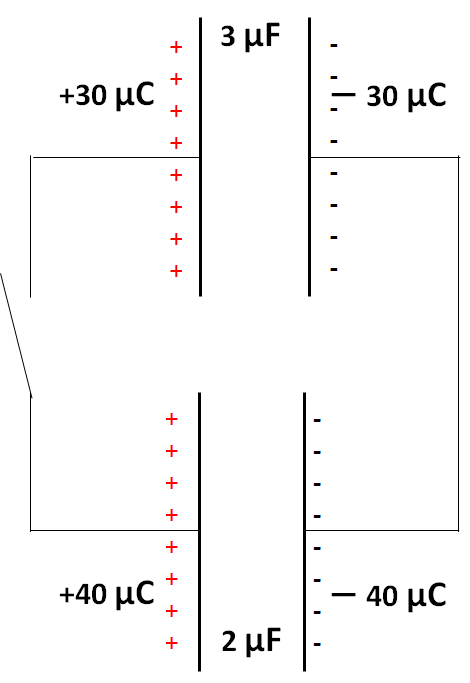
これは直列接続でしょうか?それとも並列接続でしょうか?
これは並列接続ですね。
図の左の極板は+に帯電し、右の極板は-に帯電しています。
では電荷を計算してみます。
並列であるため合成電気容量は単純な足し算です。
つまり、$合成電気容量=3+2\:\mu F$、$全電気量= 30+40 \:\mu C$
そして、電圧は共通で、$V=\dfrac{Q}{C}$ から、
$V=\dfrac{30+40}{3+2}=14\:V$
ですね!
そうすると次の図に示すような電荷分布になります。
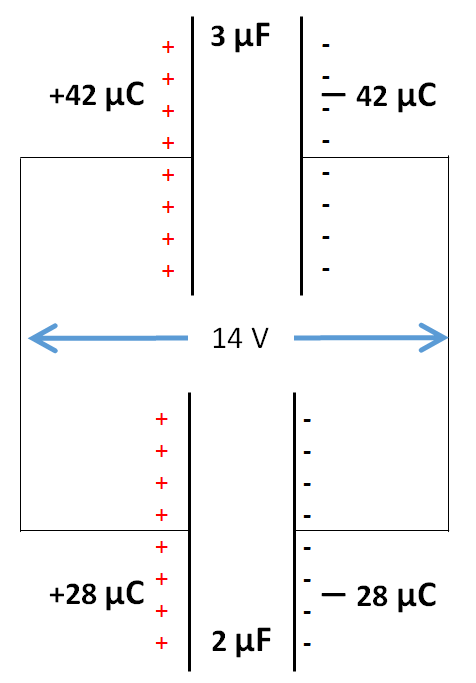
$3\:\mu F \:コンデンサー : \: Q=3\times14=42\:\mu C$
$2\:\mu F \:コンデンサー : \: Q=2\times14=28\:\mu C$
$+1\:C$ の電荷を運ぶとき $1\:J$ の仕事が必要であれば、その差は $1\:V$ の電位差があります。
このとき、次の図のように-側から+側へ (図の下から上へ)$+1\:C$ の電荷を運ぶときに、 $3 \:\mu F$ と $2\:\mu F$ のコンデンサーのどちらを通っても $14\:J$ の仕事が必要であることを示しています。
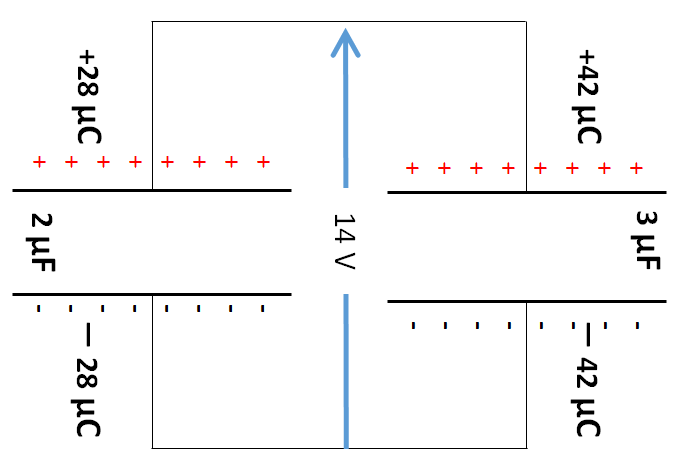
このように、図の上側が同じ符号の電荷同士、下側も同じ符号の電荷同士のときに並列というのです。
コンデンサーの接続 2
それでは、一つのコンデンサーを反転させて+の極板と-の極板同士をつなげてみましょう。
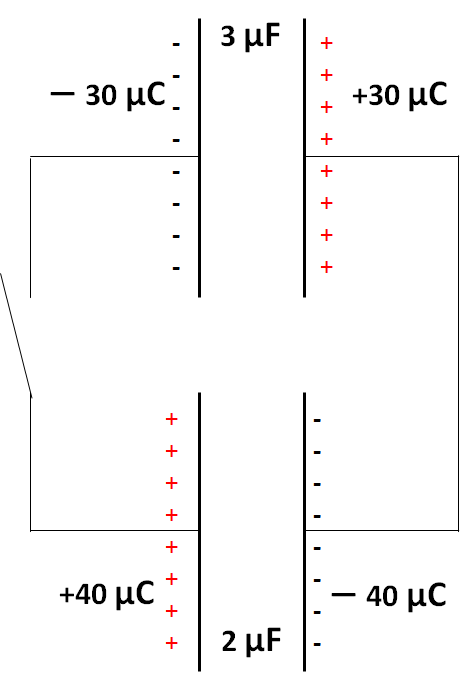
これは直列接続でしょうか?それとも並列接続でしょうか?
このとき、直列接続だと思う人が多いのですが、これは並列接続です。
なぜかというと、コンデンサーの導線で結ばれた極板同士は同電位のため同じ符号になるはずだからです。
もしも、同電位でない場合は直ちに電荷が移動して同電位になるはずです。
この場合、 $3\:\mu F$ のコンデンサーの左側の極板は-に帯電していましたが、$2\:\mu F$ のコンデンサーから電荷をもらって最終的には+になります。
つまり、極板の左側の総電気量は、$全電気量= -30+40=+10 \:\mu C$ なので左の電荷は移動しても結局+になるのです。
では電荷を計算してみます。
並列であるため合成電気容量は単純な足し算です。
つまり、$合成電気容量=3+2\:\mu F$、$全電気量= -30+40 \:\mu C$
そして、電圧は共通で、$V=\dfrac{Q}{C}$ から、
$V=\dfrac{-30+40}{3+2}=2\:V$
ですね!
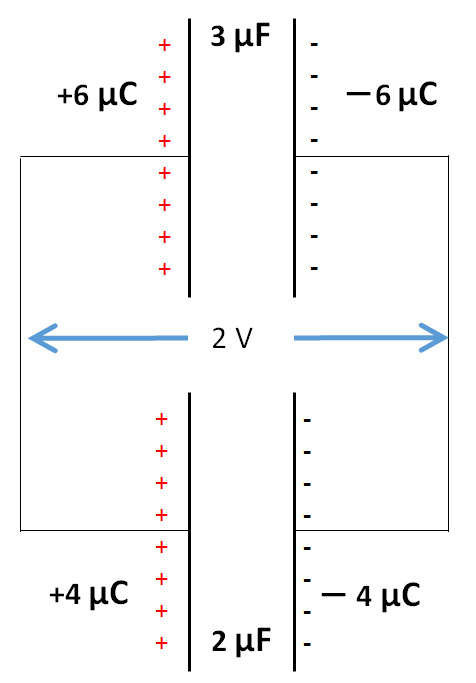
$3\:\mu F \:コンデンサー : \: Q=3\times2=6\:\mu C$
$2\:\mu F \:コンデンサー : \: Q=2\times2=4\:\mu C$
$+1\:C$ の電荷を運ぶとき $1\:J$ のエネルギーが出入りすれば、その差は $1\:V$ の電位差があります。
これも次の図のように-側から+側へ(図の下から上へ) $+1\:C$ の電荷を運ぶときに、 $3 \:\mu F$ と $2\:\mu F$ のコンデンサーのどちらを通っても $2\:J$ の仕事が必要であることを示しています。
このように、図の上側が同じ符号の電荷同士、下側も同じ符号の電荷同士のときに並列というのです。
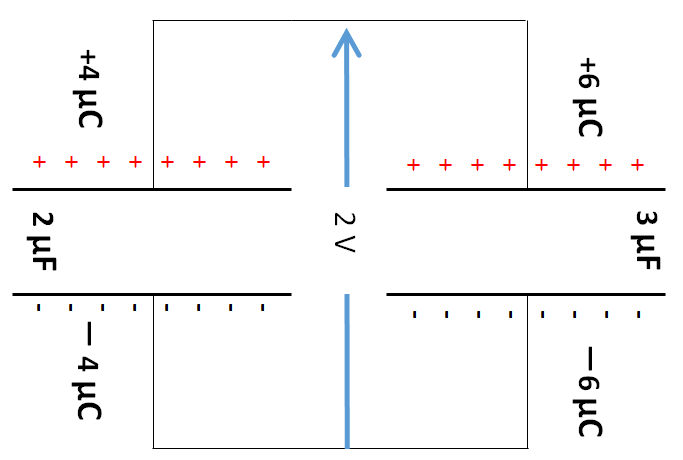
どんな場合も並列!
ここでみてきたように、単純にコンデンサー同士を接続する場合はどのような電荷であろうとどのようにつなごうと並列接続なのです。
ただし、コンデンサーの電荷どうしが打ち消し合って電荷が0になる場合もありますね。





































コメント