交流の消費電力については素子が抵抗、コイル、コンデンサーで違います。
コイルとコンデンサーの場合消費電力の時間平均は0ですから、基本的にコイルやコンデンサーでは電力を消費しません。
RLC回路の消費電力・力率については、こちらの記事へ。
交流の基礎解説シリーズについてはこちらから。
交流の消費電力
動画解説
以下で動画解説を行っています。
よろしければ、チャンネル登録お願いいたします。
交流の電圧と電流の関係
交流の電源の電圧変化 $V$ をすべての場合で、
$V=V_0\sin\omega t$
とします。ただし電圧の最大値を $V_0$ とします。
そうすると各素子(抵抗・コイル・コンデンサー)を流れる電流($I_R\:\cdot\: I_L\:\cdot\: I_C\:\:$)は
- 抵抗は同位相 $\cdots$ $\cdots$ $I_R=I_{R0}\sin\omega t$
- コイルは $\dfrac{\pi}{2}$ 遅れる $\cdots$ $\cdots$ $I_L=I_{L0}\sin(\omega t-\dfrac{\pi}{2})$
- コンデンサーは $\dfrac{\pi}{2}$ 進む $\cdots$ $\cdots$ $I_C=I_{C0}\sin(\omega t+\dfrac{\pi}{2})$
と示されます。ただし、電流の最大値をそれぞれ、$I_{R0}\:\cdot\: I_{L0}\:\cdot\: I_{C0}\:\:$ とします。

Coilとして Coil の i は late と覚えましょう。
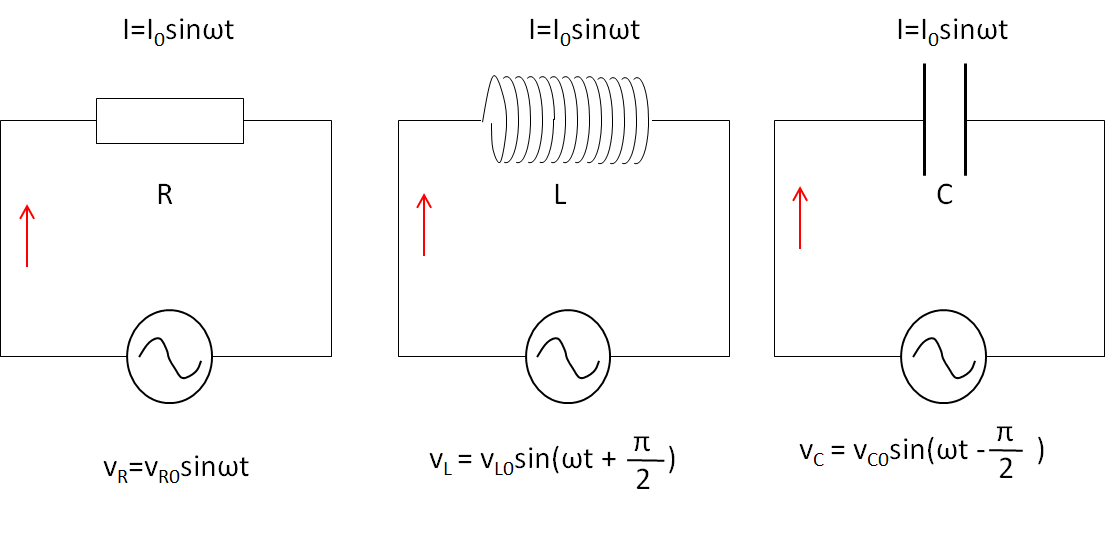
そうすると各素子(抵抗・コイル・コンデンサー)に掛かる電圧($V_R\:\cdot\: V_L\:\cdot\: V_C\:\:$)は
- 抵抗は同位相 $\cdots$ $\cdots$ $V_R=V_{R0}\sin\omega t$
- コイルは $\dfrac{\pi}{2}$ 進む$\cdots$ $\cdots$ $V_L=V_{L0}\sin(\omega t+\dfrac{\pi}{2})$
- コンデンサーは $\dfrac{\pi}{2}$ 遅れる $\cdots$ $\cdots$ $V_C=V_{C0}\sin(\omega t-\dfrac{\pi}{2})$
となります。コイルとコンデンサーの $+-$ に注意してください。
この時の位相のズレは同じなのですが、電流を基準としているため、
コイルの電圧の位相は電流に比べて $\dfrac{\pi}{2}$ 進んでいます(いいかれば、電流の位相は電圧に比べて $\dfrac{\pi}{2}$ 遅れています)。
コンデンサーの電圧の位相は電流に比べて $\dfrac{\pi}{2}$ 遅れています(いいかれば、電流の位相は電圧に比べて $\dfrac{\pi}{2}$ 進んでいます)。
抵抗の消費電力
消費電力を求めてみましょう。
まず抵抗ですが、電圧と電流に位相のズレはないので $P=IV$ より、
\begin{eqnarray}
P_R&=&I_R V_R\\
&=&I_{R0}\sin\omega t \times V_{0}\sin \omega t\\
&=&I_{R0}V_{0}\sin^2 \omega t \\\\
&=&I_{R0}V_{0}\dfrac{1-\cos 2\omega t}{2} \cdots \cdots補1\\
\end{eqnarray}
ここで、時間平均を取れば、$\cos 2 \omega t =0$ なので、
\begin{eqnarray}
P_R&=&I_{R0}V_{0}\sin^2 \omega t \\\\
&=&I_{R0}V_{0}\dfrac{1-\cos 2\omega t}{2}\\\\
&=&\dfrac{I_{R0}}{\sqrt{2}}\dfrac{V_{0}}{\sqrt{2}}\\\\
&=&I_e V_e\\
\end{eqnarray}
すなわち、$I_e=\dfrac{I_{R0}}{\sqrt{2}}$ $\:\:\:\:\:\:\:$ $V_e=\dfrac{V_{0}}{\sqrt{2}}$ とし、これらを実効値と呼びます。 こうすると交流の場合も直流の場合と同様の式を使うことができるのです。
コイルの消費電力
コイルの消費電力についても同様に計算していきましょう。
コイルの場合は電圧に対して電流の位相は $\dfrac{\pi}{2}$ だけ遅れていますからそれを考慮して、$I_L=I_{L0}\sin( \omega t-\dfrac{\pi}{2})$ より、
\begin{eqnarray}
P_L&=&I_L V_L\\
&=&I_{L0}\sin( \omega t-\dfrac{\pi}{2}) \times V_{0}\sin \omega t\\
&=&I_{L0}V_{0}\sin \omega t (-\cos \omega t) \cdots\cdots補2\\\\
&=&I_{L0}V_{0}\dfrac{-\sin 2\omega t}{2}\cdots\cdots 補3\\
\end{eqnarray}
ここで、時間平均を取れば、$\sin 2 \omega t =0$ なので、
\begin{eqnarray}
P_L&=&I_L V_L\\
&=&I_{L0}V_{0}\dfrac{-\sin 2\omega t}{2}\\
&=&0
\end{eqnarray}
ここでは、電圧に対して電流を考えて計算しましたが、電流を基準として電圧を考えても同じ答えになります。
動画解説ではそのようにしていますので参考にしてください。
コンデンサーの消費電力
コンデンサーの消費電力についても同様に計算していきましょう。
コンデンサーの場合は電圧に対して電流の位相は $\dfrac{\pi}{2}$ だけ進んでいますからそれを考慮して、$I_C=I_{C0}\sin( \omega t+\dfrac{\pi}{2})$ より、
\begin{eqnarray}
P_C&=&I_C V_C\\
&=&I_{C0}\sin( \omega t+\dfrac{\pi}{2}) \times V_{0}\sin \omega t\\
&=&I_{C0}V_{0}\sin \omega t \cos \omega t \cdots \cdots補2\\\\
&=&I_{L0}V_{0}\dfrac{\sin 2\omega t}{2}\cdots \cdots補3\\
\end{eqnarray}
ここで、時間平均を取れば、$\sin 2 \omega t =0$ なので、
\begin{eqnarray}
P_C&=&I_C V_C\\
&=&I_{C0}V_{0}\dfrac{\sin 2\omega t}{2}\\
&=&0
\end{eqnarray}
となります。
ここでも、電圧に対して電流を考えて計算しましたが、電流を基準として電圧を考えても同じ答えになります。
動画解説ではそのようにしていますので参考にしてください。
コイルとコンデンサーの消費電力
結局、交流の場合はコイルとコンデンサーでは電力消費がありません。
抵抗の場合は消費電力があります。
抵抗の消費電力ですが
$P=I_eV_e=\dfrac{I_0}{\sqrt{2}}\dfrac{V_0}{\sqrt{2}}$
$I_e=\dfrac{I_0}{\sqrt{2}}\cdots 実効値$
$V_e=\dfrac{V_0}{\sqrt{2}}\cdots 実効値$
と示されます。
RLC直列・並列回路の消費電力と力率
RLC直列回路と並列回路の消費電力について解説しています。
コイルとコンデンサーでの消費電力は 0 なので、基本的に抵抗での消費電力を考えれば OK です。
また、力率についても詳しく解説しています。




































コメント