電位差計という回路があります。
これは精密に電池の起電力を測定できるものです。
この手の回路を苦手としている人が意外と多いのですが、その原因は電位の基本的な理解があと一歩なところと、問題に慣れていないということでしょう。
ここでは、エッセンスの例題を題材にして電位差計について詳しく解説しています。
これにより、電位差計と電位の関係についてイメージできるようになり、電位差計に対する苦手意識はなくなるはずです。
直感的にイメージできるように、新しく補足の記事を作りました。そちらも御覧ください。

それではまず基礎知識として電池起電力とは何か・・から始めましょう。
教材は「物理のエッセンス 青」です。
73ページのExを見てください。
エッセンスの次は良問、そして名問がおすすめです。
Amazon
Amazon
動画で解説
動画で同じ内容について解説しています。
電池の起電力とは
まず電池の起電力について考えていきます。
ここがあやふやだと全てがあやふやになりがちです。
電池内部には一般に内部抵抗と呼ばれる抵抗 $r$ が存在します。
そのため電池内部に電流 $I$ が流れるとそこで電圧降下 $V$ が生じます。
この電圧降下は、$V=rI$ でしめされます。
しかし、電流が流れなければ電圧降下は $0$ です。
電池のもっている電圧 $E$、内部抵抗 $r$ 、流れる電流を $I$ とします。
電池内部に電流 $I$ が流れると、電池の本来持っている電圧 $E$ から $rI$ だけ電圧が下がります。
よって、電池の両端にかかる電圧 $V$ は、$V=E-rI$ と示せるはずです。

つまり、この $V$ を端子電圧、$E$ を起電力と呼んでいるのです。
起電力 $E$ とは電池に電流が流れていないときの電池電圧といえるでしょう。
ここで?が浮かびませんか?
電池とは・・・電流を流してなんぼのものなのに、電流が流れていないときの電圧って意味があるのか?
という疑問です。
しかし、この起電力は実際の回路計算でも有用であり、非常に便利な考え方なのです。
この電池の起電力さえ分かっていれば、計算によっていろいろな回路の電流値などを計算することが可能になるからなんです。
電位差計
いよいよ電位差計について解説していきましょう。
ここではエッセンスの例題(電磁気編 青 P73 Ex)を題材にしますので問題集を開いてみてください。
まず、標準電池 $E_0$ というものについて解説します。
標準電池はその起電力がよくわかっているもので、他の電池の起電力を測定するための指標となるものです。
次いで、今回測定しようとする電池についてその起電力を $E$ とします。
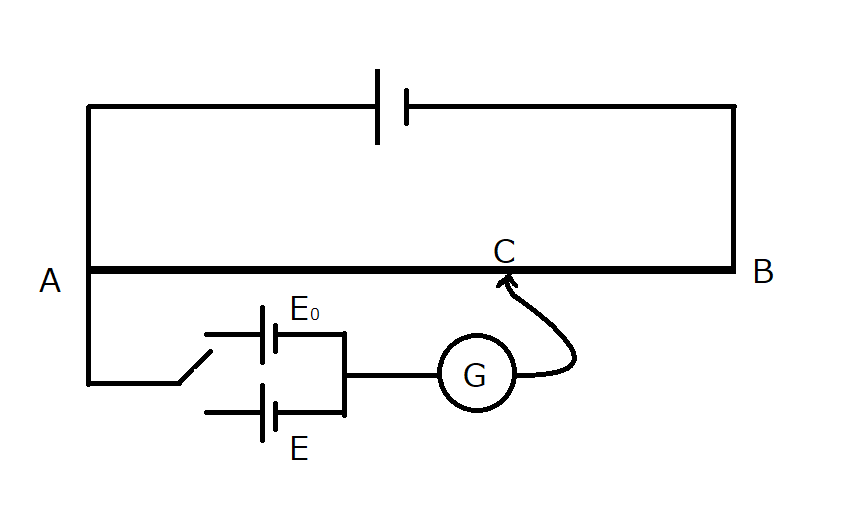
まず初めに標準電池を回路につなぎ、探針を動かして線抵抗AB上で検流計G に電流が流れなくなる点 C を探します。
その時の A からの長さを精密に測定しておきましょう。ここでは $l_0$ とします。
次に、測定したい電池を(起電力 $E$ )を標準電池の代わりに回路につなぎます。
そして、同じように探針を動かして、検流計G に電流が流れなくなる位置 C’ を探します。
この時の A からの距離を $l$ とします。
さて、これだけで未知の電池の起電力を測定することができるのですが、そのやり方は、
- AB間の抵抗に電流が流れるとき、 AC・AC’ 間で電圧降下が生じている
- 電池を AC・AC’ に並列につないでも電流が流れないことから電池の起電力(電流0の場合の電圧)と AC・AC’ 間の電圧降下が等しいとわかる。この詳しい説明は次章を見てください。
- 標準電池をつないだ時、AC 間に流れる電流を $I$ として AC 間での電圧降下は $E_0=IR_{E_0} $ となる(このときの、AC 間の抵抗を $R_{E_0}$ とし、AC の長さを $l_0$ とする)。

- 次に標準電池の代わりに未知の電池をつないだ時、やはり電池に電流は流れないのだからAC’ 間に流れる電流は同じ $I$ である。
- したがって、$E=IR_{E}$ である。(このときの、AC’ 間の抵抗を $R_{E}$ とし、AC’ の長さを $l$ とする)
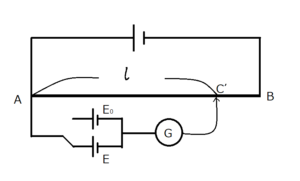
- 抵抗はその長さに比例する($R=\rho\dfrac{l}{S}$ $\rho$ と $S$ は共通)ので、$R_{E_0}:R_{E}=l_0:l$ となる。
- 起電力の比をとると、
$\begin{split}E_0:E=&IR_{E_0}:IR_{E}\\\\
=&R_{E_0}:R_{E}\\\\
=&l_0:l
\end{split}$
よって、
$E=\dfrac{l}{l_0}E_0$
となります。
どうして電流が流れないのか?
このことについて、なんだかもやもやした疑問を持っている人が多いようですね。
ちょっとここで考えてみましょう。
直感的にイメージできるように、新しく補足の記事を作りました。そちらも御覧ください。

まず、普通の回路では電流は電位の高いほうから低いほうへ流れます。
電位が同じであれば電流は流れません。
このことを水の流れで考えてみましょう。
水は高いところから低いところへ流れ、その逆は自然にはありません。
もし高さが同じなら水は流れずよどんでいるでしょう。
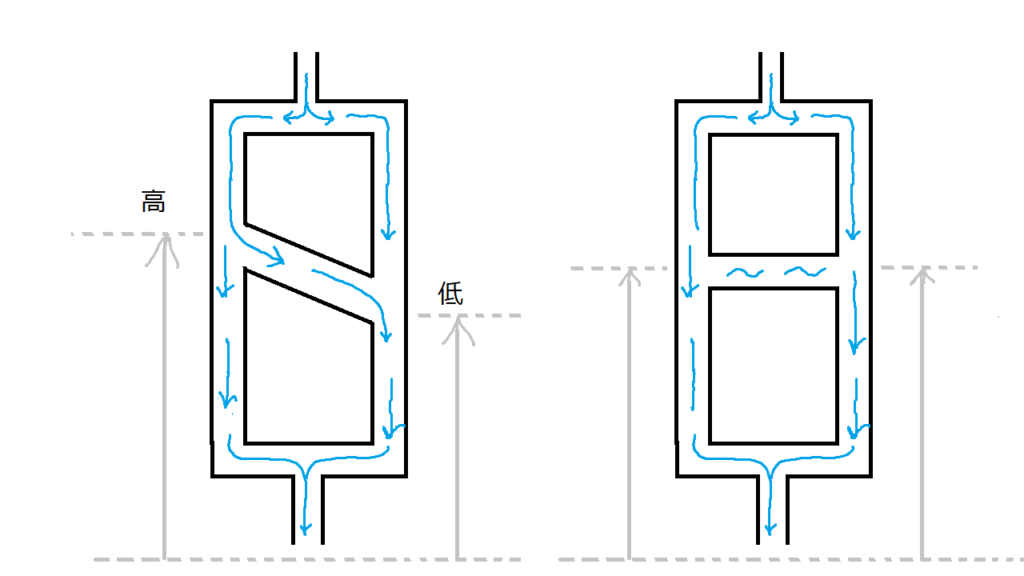
同様に、電流も電位の高いところから低いところへ流れます(電池の内部は逆です)。
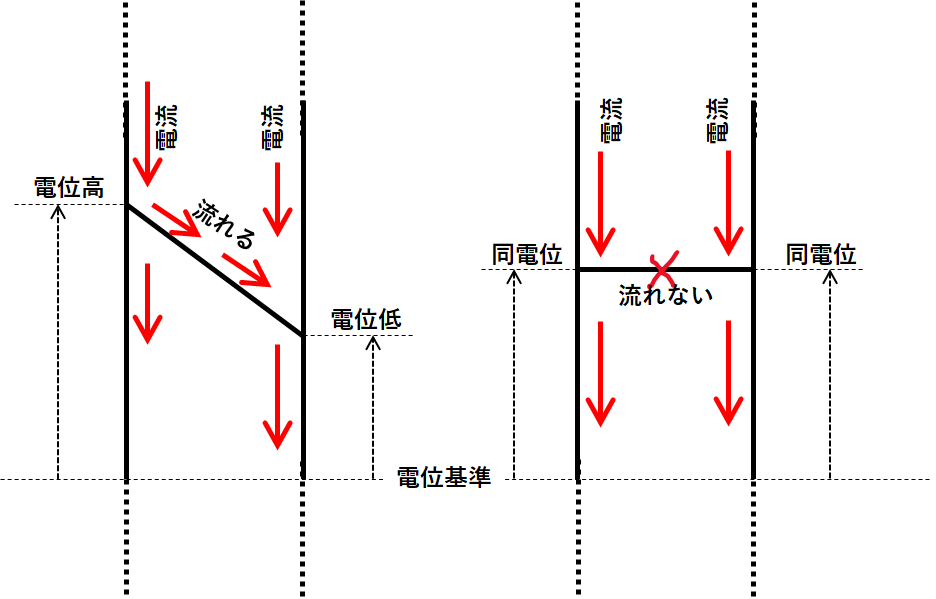
さて、同じことをこの電位差計について考えてみます。
わかりやすくするため、図を縦にしてみましょう。

電位基準点を B にしてみます。
そうすると、C’ 点で電流が流れないのだから、図の電池側も AB の線抵抗側も B からの電位の高さは同じになります。
さらに、A 点は電池側と線抵抗側は同電位です(つまり B からの高さは同じです)。
したがって残りの電池の部分と AC’ 抵抗分は同じ電位差になります。
つまり、C’からみた電池周りの電位の高さも、AC’ 周りで見た電位の高さも同じだということです。
接点をずらしたときの電流の流れる向き
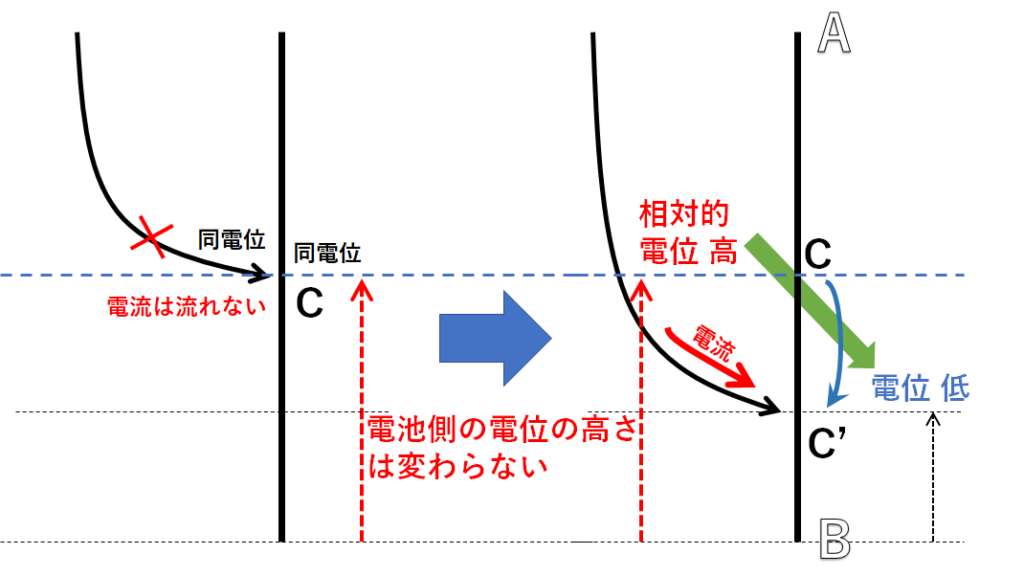
ついでに言えば、この考え方を応用すると、C 点をずらしたときにどちらからどちらへ電流が流れるのかがわかります。
電流は電位の高いほうから低いほうへ流れるのですから、図で C を B 側にずらしてやると、抵抗側の電位が低くなり、電池 → 抵抗側 に電流が流れます。
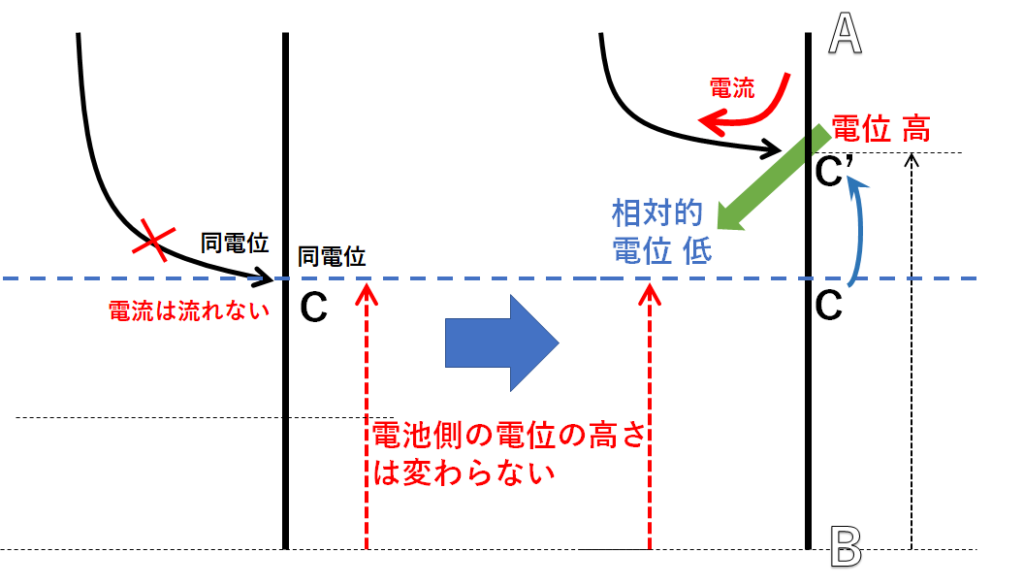
同様に、図で C を A 側にずらしてやると、抵抗側の電位が高くなり、抵抗側 → 電池 に電流が流れます。
電流が流れないのに測れる?
この装置の特徴は、電流が流れない点を探していることです。
おもしろいですね。
なんといっても、測定対象の電池に一切電流を流さないのに起電力が測定ができるのが不思議でもあり、巧妙な仕掛けだと感心するところです。
というか、電池の起電力自体は電流が流れないときの電圧なのですから、正確な測定のために当然といえば当然といえるかもしれません。もし少しでも電流を流して測定する・・・というのであれば、内部抵抗による電圧降下が生じて誤差が大きくなるはずです。
つまり、いかに微弱な電流さえも流れないように気を付けて測定できるか・・・にこの実験の精度がかかっています。だから、電流の検知には鋭敏な検流計 G を使うのです。
似たような考え方をするものにホイートストンブリッジがあります。
こちらも電流が流れないのを測定する・・・というところに意味があるのは同様です。

まとめ
電位差計は電流が流れないのに測定ができる。
いかに電流を流さないようにするかに測定の精度がかかっている。
図で検流計Gに電流が流れないときのAC間の長さを測定する。
標準電池 $E_0$ と 未知の電池 $E$ とで、それぞれ $l_0$、$l$ とした場合、


$E_0:E=l_0:l$
$E=\dfrac{l}{l_0}E_0$
である。
もっと直感的にイメージできるように、新しく補足の記事を作りました。そちらも御覧ください。






































コメント
非常に分かりやすかったです。
電位差計は計算はできるのですが、イメージは掴めず、すぐに忘れてしまって困ってました。
水の流れで電位差計を捉えたことは初めてでしたが、丁寧に解説してくださったおかげで理解できました。本当にありがとうございます。他の分野も参考にさせていただきます♀️♀️
受験生さま
ありがとうございます!