高校物理公式集

2022.12.12

スポンサーリンク

高校物理公式集

「公」式を丸暗記してもほとんど役立ちません。
なぜかを問い、式を理解しましょう。（暗記は、やはり必要ですが…）

力学

速度の分解

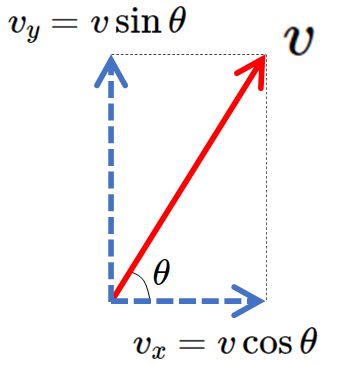
  • $v_x=v\cos\theta $
  • $v_y=v\sin\theta $
  • $v=\sqrt{{v_x}^2 + {v_y}^2}$

 

 

相対速度

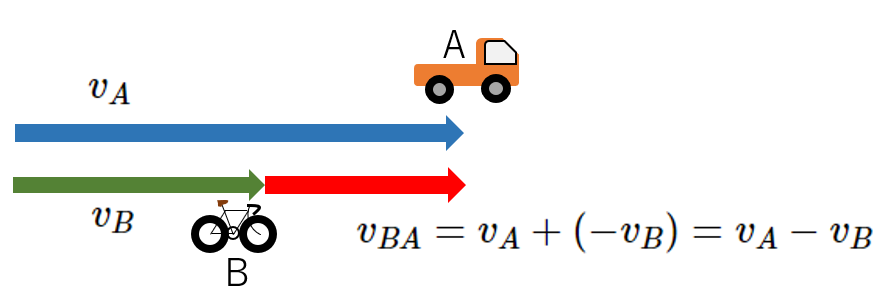
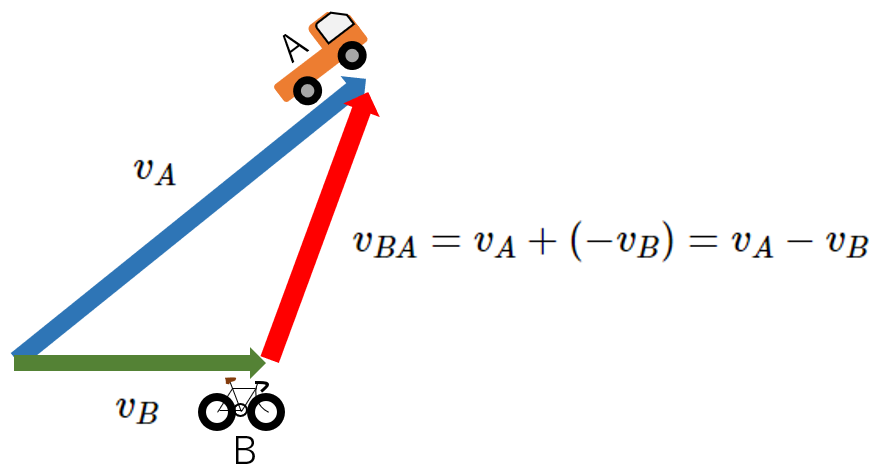
  • $\overrightarrow{v_{BA}}=\overrightarrow{v_A} \:-\: \overrightarrow{v_B}$

速度と加速度の基本式

  • $v=\dfrac{\Delta x}{\Delta t}$
  • $a=\dfrac{\Delta v}{\Delta t}$。
  • $v=v_0+at$
  • $x=v_0t + \dfrac{1}{2}at^2$
  • $v^2-{v_0}^2=2ax$

重力を受ける場合

基本式で $a \rightarrow  \pm g$ と書き換えます。
また、必要であれば $x \rightarrow y$ と書き換えましょう。

自由落下・鉛直投げ上げ・鉛直投げ下ろし
    • $v=v_0 \pm gt$
    • $y=v_0t \pm \dfrac{1}{2}gt^2$
    • $v^2-{v_0}^2= \pm 2gy$

自由落下では　$v_0=0$  

一般に各運動の初速度方向（自由落下は鉛直下方向）を正にとります。

      • 自由落下･･･ $+g$
      • 鉛直投げ上げ･･･ $-g$
      • 鉛直投げ下ろし･･･ $+g$
斜方投射・水平投射

鉛直方向と水平方向に分解して考えます。

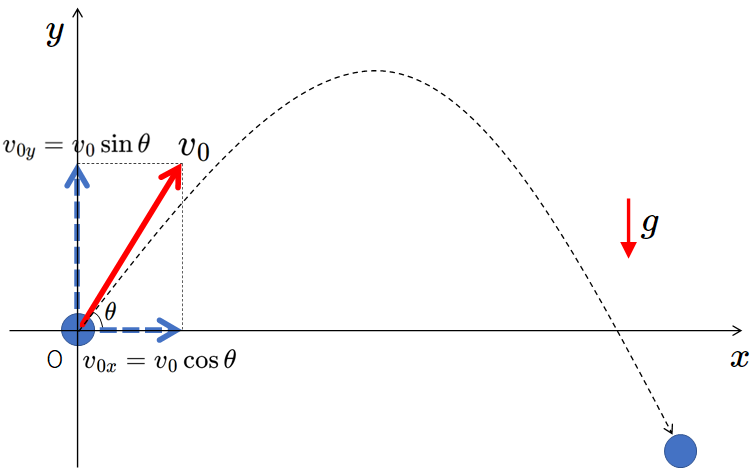
    • 鉛直方向 ･･･ 自由落下・鉛直方向への投げ上げ、投げ下ろし
      • $v_{y}=v_{0y} \pm gt$
      • $y=v_{0y}t \pm \dfrac{1}{2}gt^2$
      • ${v_{y}}^2-{v_{0y}}^2= \pm 2gy$

$g$ については、自由落下・鉛直投げ上げ・鉛直投げ下ろしと同様に、向きを考えて正負をつけます。

    • 水平方向 ･･･ 等速直線運動　$x=v_{0x}t$
    • 軌道方程式 ･･･ $x$ と $y$ の式から時間 $t$ を消去します。

   $y=\tan\theta \cdot x \:-\: \dfrac{g}{2{v_0}^2\cos ^2 \theta}\cdot x^2$

    • 水平投射は斜方投射の特殊バージョンと考えましょう。

運動方程式

  • $m\overrightarrow{a}=\overrightarrow{F}$

摩擦力

  • 最大摩擦力　$F_0=\mu N$
  • 運動摩擦力　$F^{\prime}=\mu^{\prime}N$
  • 摩擦角 $\theta_0$ と静止摩擦係数 $\mu$　　$\mu=\tan\theta_0$

重力 $W$

  • $W=mg$

エネルギーの原理

  • $\dfrac{1}{2}mv^2+W=\dfrac{1}{2}m{v^\prime}^2$

位置エネルギーと運動エネルギー

  • 位置エネルギー　$U=mgh$
  • 運動エネルギー　$K=\dfrac{1}{2}mv^2$
  • ばねの位置エネルギー　$U_k=\dfrac{1}{2}kx^2$
  • 力学的エネルギー保存則
    $mgh+\dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2=$一定

フックの法則 

  • $F=kx$　　$k$：ばね定数
  • 合成ばね定数 $k$ 

 

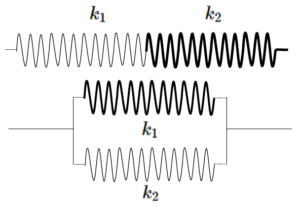
  • 直列　$\dfrac{1}{k}=\dfrac{1}{k_1}+\dfrac{1}{k_2} + \cdots$

 

  • 並列　$k=k_1+k_2+ \cdots$

圧力

  • 圧力は単位面積当たりの力　　$p=\dfrac{F}{S}$

水圧

  • $p=\rho hg$　　水圧の差が浮力となる

浮力

  • $F=\rho Vg$　　浮力の大きさは水深に無関係

剛体

  • 力のモーメント　$M=Fl$
  • 偶力のモーメント　$M=Fl$
  • 重心

  $x_G=\dfrac{m_1x_1+m_2x_2+m_3x_3+\cdots}{m_1+m_2+m_3+\cdots}$

  $y_G=\dfrac{m_1y_1+m_2y_2+m_3y_3+\cdots}{m_1+m_2+m_3+\cdots}$

運動量と力積

  • 運動量　$m\overrightarrow{v}$
  • 力積　$\overrightarrow{F}\Delta t$
  • 運動量と力積　$m\overrightarrow{v} + \overrightarrow{F}\Delta t=m\overrightarrow{v^\prime}$
  • 運動量保存則　
    $m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}+m_3\overrightarrow{v_3}+\cdots $
    $\:\:\:\:\:\:=m_1\overrightarrow{v_1^\prime}+m_2\overrightarrow{v_2^\prime}+m_3\overrightarrow{v_3^\prime}+\cdots$
  • 反発係数 $e$   　$e=-\dfrac{v^\prime}{v}$
    $e=-\dfrac{v_1^\prime-v_2^\prime}{v_1-v_2}$

円運動

  • 角速度　$\omega=\dfrac{\theta}{t}$　　$\theta=\omega t$
  • 周期　$T=\dfrac{2\pi}{\omega}$
  • 回転数　$n=\dfrac{1}{T}$
  • 速さ　$v=r\omega=\dfrac{2\pi r}{T}$

    速くてブルー　⇒　$v=r\omega$

  • 加速度の大きさ　$a=v\omega=r\omega^2=\dfrac{v^2}{r}$

    加速度アルウ$^2$　⇒　$a=r\omega^2$

  • 向心力
    $F=ma=mv\omega=mr\omega^2=m\dfrac{v^2}{r}$
  • 慣性力　$-ma$
  • 遠心力の大きさ
    $F=ma=mv\omega=mr\omega^2=m\dfrac{v^2}{r}$

単振動

  • 周期　$T=\dfrac{1}{f}=2\pi\sqrt{\dfrac{m}{K}}$
  • 変位　$x=A\sin\omega t$
  • 速度　$v=A\omega\cos\omega t$
  • 加速度　$a=-A\omega^2\sin\omega t=-\omega^2x$
  • 復元力
    $F=ma=-mA\omega^2\sin\omega t$
    $\:\:\:=-m\omega^2x=-Kx$
  • 角振動数　$\omega=\sqrt{\dfrac{K}{m}}$
  • 単振り子　$T=\dfrac{1}{f}=2\pi\sqrt{\dfrac{l}{g}}$

万有引力

  • ケプラーの法則　$\dfrac{T^2}{a^3}=k$　一定
  • 面積速度一定
    $\dfrac{1}{2}rv\sin\theta=k$　一定
  • 万有引力　$f=G\dfrac{m_1m_2}{r^2}$
  • 重力($M$：地球質量　$R$ ：地球半径)
    $mg=G\dfrac{Mm}{R^2}$ ，$GM=gR^2$
  • 万有引力による位置エネルギー　$U=-G\dfrac{Mm}{r}$
  • 万有引力による力学的エネルギー保存の式
    $\dfrac{1}{2}mv^2+\left( -G\dfrac{Mm}{r} \right) =$一定

波動

波動基礎

  • 波の振動数と周期　$T=\dfrac{1}{f}$
  • 波の速さ　$v=f\lambda$
  • $x$の正の向きに進む正弦波の式
    $y=A\sin\dfrac{2\pi}{T}\left(t-\dfrac{x}{v} \right)$
    $\:\:\:\,=A\sin2\pi\left(\dfrac{t}{T}-\dfrac{x}{\lambda} \right)$
  • $x$の負の向きに進む正弦波の式
    $y=A\sin\dfrac{2\pi}{T}\left(t+\dfrac{x}{v} \right)$
    $\:\:\:\,=A\sin2\pi\left(\dfrac{t}{T}+\dfrac{x}{\lambda} \right)$
  • 波の重ね合わせの原理　$y=y_1+y_2$
  • 波の反射　固定端 → 位相$2\pi$変化（位相反転），自由端 → 位相変化なし

音

  • 音速　$V=331.5+0.6t$
  • うなり　$f=|f_1-f_2|$
  • ドップラー効果
    $f^\prime=\dfrac{V-v_O}{V-v_S}f$ ，　$\dfrac{V-v_S}{f}=\dfrac{V-v_O}{f^\prime}=\lambda^\prime$
  • 風がある場合のドップラー効果
    $f^\prime=\dfrac{(V\pm V_w)-v_O}{(V\pm V_w)-v_S}f$　　風の向き：$+$　風と逆向き：$-$

光

  • 反射の法則　$i=j$
  • 屈折の法則
    $n_{12}=\dfrac{\sin i}{\sin r}=\dfrac{v_1}{v_2}=\dfrac{\lambda_1}{\lambda_2}=\dfrac{n_2}{n_1}$
  • 屈折の法則　$n_1\sin i=n_2\sin r$
  • 全反射（臨界角 $i_0$）　$n_1\sin i_0=n_2\sin 2\pi=n_2$　　屈折角が $2\pi$
  • 見かけの深さ　$h^\prime=\dfrac{h}{n}$
  • 写像公式　$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$　　倍率　$m=\left| \dfrac{b}{a} \right|$
    虚像：b<0　凸レンズ・凹面鏡：f>0　凹レンズ・凸面鏡：f<0
  • 干渉の式　|経路差|$=m\lambda$ ， $m\lambda + \dfrac{1}{2}\lambda$
    強めあう OR 弱めあうは波源の振動や波の反射を考慮して決める　$(m=0,1,2,3,\cdots)$　　$\lambda$は経路差中の値

熱

熱基礎

  • ボイル・シャルルの法則
    $\dfrac{pV}{T}=$一定
  • 理想気体の状態方程式　$pV=nRT$
  • ボルツマン定数　$k=\dfrac{R}{N_A}$
  • 気体分子の平均運動エネルギー　$\dfrac{1}{2}m\overline{v^2}=\dfrac{3}{2}kT$
  • 単原子分子気体の内部エネルギー
    $U=\dfrac{3}{2}nRT$ ，　$\Delta U=\dfrac{3}{2}nR\Delta T$
  • 気体がする仕事 $W$ とされる仕事 $W^\prime$ 　$W=-W^\prime$
  • 熱力学第一法則
    $\Delta U=Q+W$ ，　$Q=\Delta U +W^\prime$
  • 定積モル比熱　$\Delta U=nC_V\Delta T$
  • 定圧モル比熱　$Q=nC_p\Delta T$
  • マイヤーの関係式　$C_p=C_V+R$
  • 単原子分子　$C_V=\dfrac{3}{2}R$ ，　$C_p=\dfrac{5}{2}R$
  • 2原子分子　$C_V=\dfrac{5}{2}R$ ，　$C_p=\dfrac{7}{2}R$
  • ポアソンの法則　$pV^\gamma =$一定
  • 比熱比　$\gamma=\dfrac{C_p}{C_V}$
  • 熱効率　$e=\dfrac{W^\prime}{Q_{in}}=\dfrac{Q_{in}-Q_{out}}{Q_{in}}$
  • 熱力学第二法則　熱は高温の物体から低温の物体へ移動し、自然に低温の物体から高温の物体へ移動することはない。エントロピーは増大する。

電磁気

電場と電位

  • 静電気力　$f=k\dfrac{q_1q_2}{r^2}$
  • 点電荷 $Q$ 周りの電場　$E=k\dfrac{Q}{r^2}$
  • 電場から受ける力　$\overrightarrow{F}=q\overrightarrow{E}$
  • ガウスの法則　$N=4\pi k Q=\dfrac{Q}{\varepsilon}$
  • 電位　$V=\dfrac{U}{q}$
  • 一様な電場　$E=\dfrac{V}{d}$

    $Ed=V$　⇒　江戸でビクトリー

  • 点電荷周りの電位　$V=k\dfrac{Q}{r}$

コンデンサー

電流

  • 電流　$I=\dfrac{Q}{t}$ ，　$I=envS$

    $I=vSne$　⇒　わたしはブスねー

  • オームの法則　$V=RI$ 
  • 抵抗率 $\rho$　$R=\rho\dfrac{l}{S}$
  • 電力　$P=\dfrac{W}{t}=IV=I^2R=\dfrac{V^2}{R}$
  • 電力量　$W=Pt=IVt=I^2Rt=\dfrac{V^2}{R}t$
  • 1キロワット時(kWh)　1000Wで1時間仕事をした場合のエネルギー量
  • 直列抵抗の合成　$R=R_1+R_2+\cdots$
  • 並列抵抗の合成　$\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\cdots$
  • 電池の起電力　$E=V+rI$
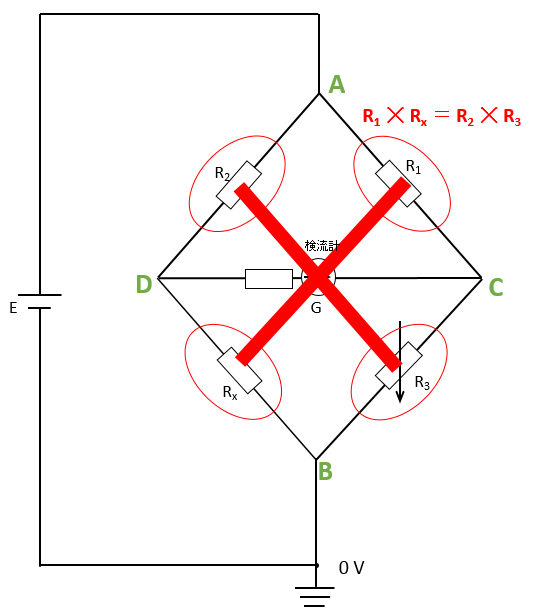
  • ホイートストンブリッジ　$R_1\times R_x=R_2 \times R_3$

磁場

線に$\pi$あり

円に$\pi$なし　　

ソレノイドは「エッチ(H)な私(nI)」??

  • 磁束密度　$\overrightarrow{B}=\mu \overrightarrow{H}$
  • 比透磁率 $\mu_r$ 　　$\mu=\mu_r \mu_0$
  • 磁束　$\Phi=BS$
  • 電流が受ける力　$F=\mu IHl=IBl$

    $BIl=F$　⇒　ビールは力

  • ローレンツ力　$f=qvB$

    $f=Bvq$　⇒　力はバーベキュー

電磁誘導

交流

  • 実効値　$V_e=\dfrac{1}{\sqrt{2}}V_0$ ， $I_e=\dfrac{1}{\sqrt{2}}I_0$
  • 電力　$\overline{P}=\dfrac{1}{2}I_0V_0=I_eV_e$
  • 変圧器　$V_1:V_2=N_1:N_2$
  • コイルリアクタンス　$X_L=\omega L$
  • コンデンサーリアクタンス　$X_C=\dfrac{1}{\omega C}$
  • RLC直列回路のインピーダンス
    $Z=\sqrt{R^2+\left( \omega L- \dfrac{1}{\omega C} \right)^2}$
  • RLC並列回路のインピーダンス
    $Z=\dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left( \omega C – \dfrac{1}{\omega L} \right)^2}}$
  • 力率 $\cos\phi$ 　$\overline{P}=I_eV_e\cos \phi$
  • 共振周波数・固有周波数　$f=\dfrac{1}{2\pi\sqrt{LC}}$ ， $T=\dfrac{1}{f}$
  • 電気振動のエネルギー保存則
    $\dfrac{1}{2}LI^2+\dfrac{1}{2}CV^2 $
    $\:\:\:\:\:=\dfrac{1}{2}LI_0^2=\dfrac{1}{2}CV_0^2=$ 一定

原子

原子

  • 光速　$c=\nu \lambda$
  • 光子のエネルギー　$E=h\nu$
  • 光子の運動量　$p=\dfrac{E}{c}=\dfrac{h\nu}{c}=\dfrac{h}{\lambda}$
  • ド・ブロイ波長　$\lambda=\dfrac{h}{p}=\dfrac{h}{mv}$
  • 光電効果　$h\nu=K_0+W$
  • 電子ボルト　1eV$=1.60 \times 10^{-19}\:$J
  • X線の最短波長
    $eV=E=h\nu=\dfrac{hc}{\lambda_0}$
    $\lambda_0=\dfrac{hc}{eV}$
  • ブラッグの条件　$2d\sin\theta = n\lambda\:\:\:\:\:\:\: (n=1,2,3,\cdots)$
  • コンプトン効果
    $\Delta \lambda =\lambda^\prime – \lambda = \dfrac{h}{mc}(1-\cos\theta)$
  • 量子条件
    $2\pi r=n\lambda = n \cdot \dfrac{h}{mv} $
      $\:\:\:\:\: {(n=1,2,3,\cdots)}$
  • 振動数条件　$h\nu = E_n-E_n^\prime $
  • 軌道半径　$r=\dfrac{h^2}{4\pi^2k_0me^2}\cdot n^2$
  • エネルギー準位
    $E_n = -\dfrac{2\pi^2k_0^2me^4}{h^2}\cdot \dfrac{1}{n^2} $
    $\:\:\:\:\:\:\,=-\dfrac{Rch}{n^2} \:\:\:\:\:{(n=1,2,3,\cdots)}$  

    軌道半径やエネルギー準位は、覚えなくてもいい。

    $n^2$ に関係して、とびとびの値をもつことは意識しましょう。

  • 半減期　$N=N_0\left( \dfrac{1}{2} \right)^{\dfrac{t}{T}}$
  • 質量とエネルギー　$E=mc^2$

コメント