運動量
エネルギーの記事(運動エネルギーに $\frac{1}{2}$ がつくのはなぜ)でも述べましたが、かつて「活力論争」といわれる議論がありました。
すなわち、物体の勢いを示す「活力」を質量 $m$ と速度 $v$ を使って、 $mv$ と示すべきか、あるいは、$mv^2$ とすべきか・・についての論争です。
これは、「活力論争」とも呼ばれ、50年以上にも及ぶ議論を巻き起こしたのです。
この論争はのちに、$mv$、$mv^2\:\:(\frac{1}{2}mv^2)$ どちらも正しいとして決着がついています。
さて今回のお題である、運動量について、
教科書などの記述を見てみましょう。
物体の勢いを表す量の一つとして、「質量×速度」という量を考え、これを運動量という。
という感じで唐突に出てきます。そして、これだけです。

正直、当時私は、「??なぜ??」が頭の中にいっぱいになり、
どうにも気になって先に進めませんでした。
なぜ、唐突に 質量×速度 などという物理量を思いついたのか??
・・・というのがその当時の疑問です。
冒頭に述べたように、運動量とエネルギーに関しては50年以上にも及ぶ「活力論争」があったわけですから、いきなり一言、わけのわからないことを言われても、やはり普通の人は拒絶反応を示してしまいますよね。
そのような物理学上の大問題を、たった一行・一言で、「こういうものだから辛抱して覚えろ」とでも言わんばかりですが、これでは、面白い!とは程遠く、物理を好きになれ・・などというのも難しい気がします。
ほんの少しでもいいから、科学の歴史的なことに触れてくれていれば、もっとすんなり入っていけたのではないでしょうか?

では、運動量 $mv$ を導いてみましょう。
ニュートンの運動方程式 $ma=F$ はよろしいですね。
ここで加速度 $a$ の定義から、$a=\dfrac{v-v_0}{\Delta t}$ を代入してみます。
図にあるように物体の質量 $m$ 、速度はそれぞれ、$v,\:v_0$ です。
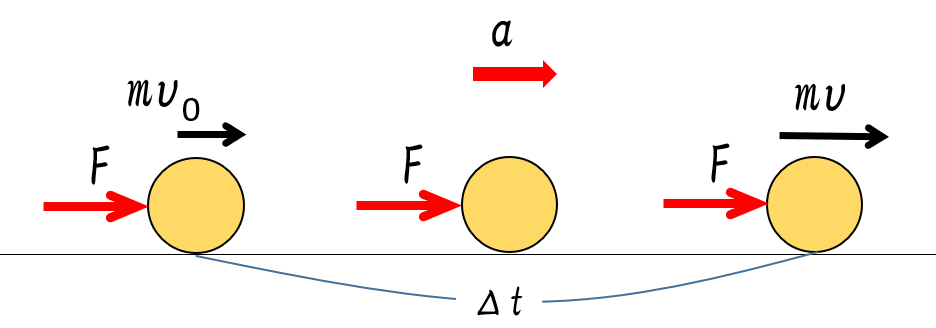
そうすると、
\begin{eqnarray}
ma&=&F\\\\
m\left(\dfrac{v-v_0}{\Delta t} \right)&=&F\\\\
mv-mv_0&=&F\Delta t \\\\
\end{eqnarray}
より、
$mv_0+F\Delta t=mv$
となります。
このとき、$mv$ を運動量 $p$ と、$F\Delta t$ を力積 $I$ と呼ぶことにしたのです。
したがって、力積と運動量の関係は、
$p_0+I=p$
$mv_0+F\Delta t=mv$
と書けます。
これは日本語でいうと、(最初の運動量)+力積=(後の運動量) という意味ですね。
力積
さて、力積とは上に述べたように、$F\Delta t$ で示される量です。
つまり、力×時間 というわけですね。
$p_0+I=p$
$mv_0+F\Delta t=mv$
は、ある運動量を持った物体に、力積として、時間 $\Delta t$ の間、力$F$ を作用させると、運動量が変化する。
ということを述べています。
また、速度や力はベクトル量であるため、
$\vec{p_0}+\vec{I}=\vec{p}$
$m\vec{v_0}+\vec{F}\Delta t=m\vec{v}$
が成り立ちます。
これは直線上だけではなく、2次平面や3次元空間でも成り立ちます。
ちなみに、運動エネルギーと仕事の関係は、
$\dfrac{1}{2}mv^2_0+Fx=\dfrac{1}{2}mv^2$
$K_0+W=K$
ある運動エネルギーを持った物体に、距離 $x$ の間、力$F$ を作用させると、運動エネルギーが変化する。
ということを述べています。
ようするに、力積は力と時間、仕事は力と距離 によって決まる、ということを示しています。
そうして、それらが作用した結果、運動量や運動エネルギーが変化する・・・というわけです。
力積と運動量
力積と運動量の関係式の素晴らしいところは、例えば、バットでボールを打つ・・などという、非常に短い時間で複雑な運動をすると考えられる場合に、バットで打つ前と打った後の速度さえわかれば解析ができる、という点です。
図のように、バットでボールを打つという複雑な運動が行われるとき、かかる力の平均を求めることができます。
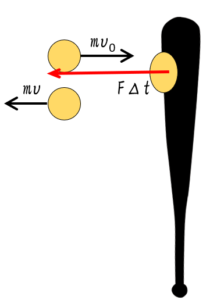
そしてその時の力積のグラフは次のような図になると考えられます。
縦軸はボールが受ける力(バットが受ける力)、横軸は接触時間です。
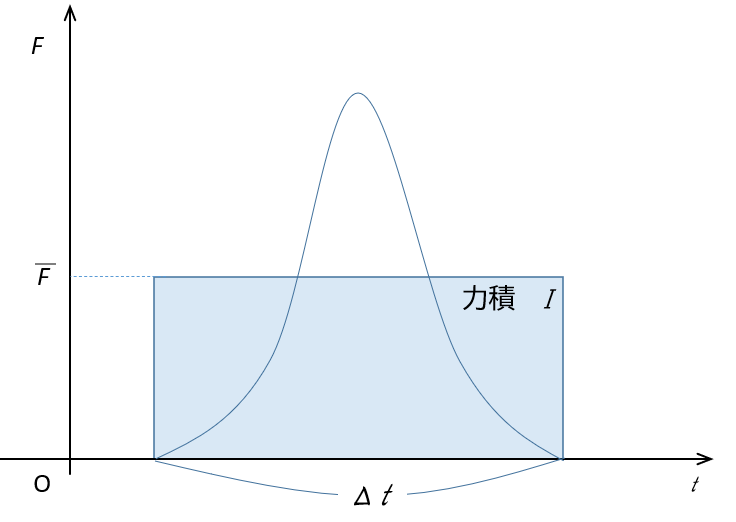
図の曲線の囲む面積と、色を付けた四角の面積が等しいとき、$\overline{F}$ を平均の力とできます。
したがって、ボールとバットの接触時間がわかれば、かかる力の平均を求めることが可能です。
つまり、
$F\Delta t=mv-mv_0$
より、
$\overline{F}=\dfrac{mv-mv_0}{\Delta t}$
あるいはその逆も可能。つまり、平均の力から接触時間を求めることもできますね。
運動量保存則
衝突や爆発などの前後において、系の運動量の総和が保存される「運動量保存則」についてはこちらの記事を参照してください。








































コメント