単スリットというのは普通、教科書には記載されていませんし、参考書にもあまり解説されていません。しかし、難関といわれるところではときどき出題されます。一度目を通しておいて損はありません。
単スリットの回折・干渉
二重スリットと単スリットの回折条件
スリットによる干渉条件です。$\lambda$ 光の波長 $\theta$ 回折角
光源として、一次スリットを通った光を用いるかレーザー光を利用します。
- 二重スリットの干渉条件
- $d\sin\theta = m\lambda $ 明線 強めあう
- $d\sin\theta = m\lambda + \dfrac{\lambda}{2}$ 暗線 弱めあう
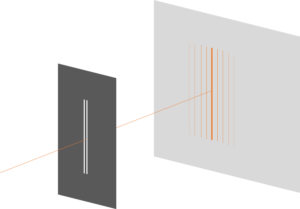
$d$ はスリットの間隔(格子定数)
ただし $m=0, \: \pm 1,\: \pm 2,\: \pm 3,\: \cdots \cdots $
こちらを参考にしてください。

- 単スリットの干渉条件
- $d\sin\theta = m\lambda $ 暗線 弱めあう
- $d\sin\theta =m\lambda + \dfrac{\lambda}{2}$ 明線 強めあう( $\theta=0$ のときを含む)
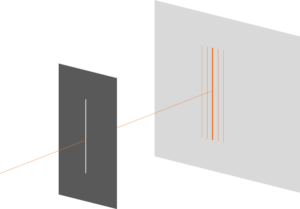
$d$ は単スリットの幅を示す
ただし $m=\pm 1,\: \pm 2,\: \pm 3,\: \cdots \cdots $
0 を含まず
二重スリットと単スリットではその干渉条件が逆になっていることに注意します。
単スリット
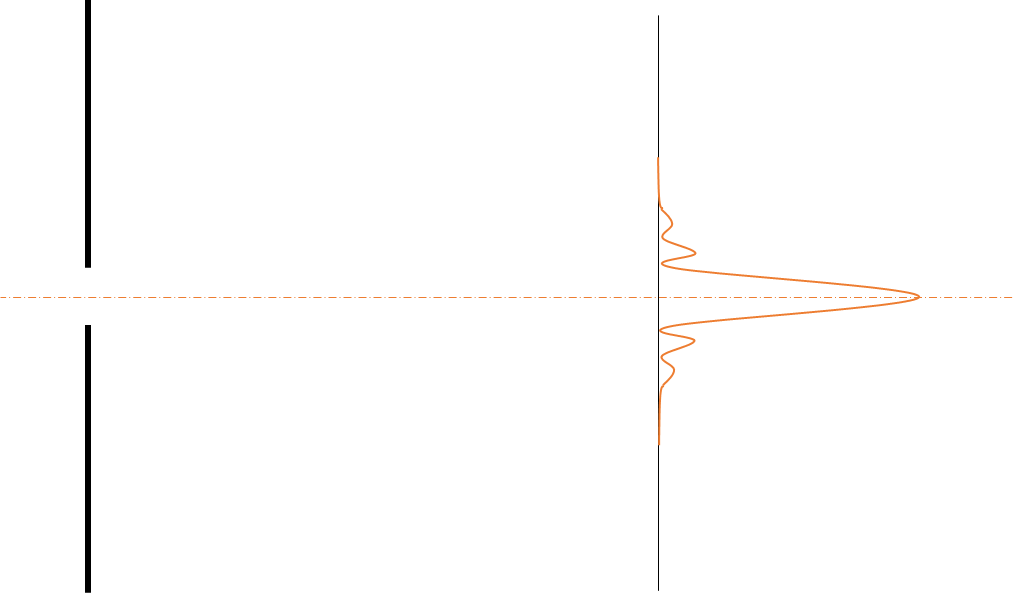
単スリットの干渉縞
単スリットというのは、文字通り一つの隙間しかないスリットのことです。
光は単スリットで干渉して、次図のようにスクリーン上に明暗の縞を作ります。
ただし、明線の明るさは中央から離れるに従って急激に減少します。
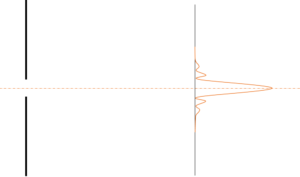
スリットが1つしかないのに干渉するの!?という疑問、もっともです。
私も最初に見たときにはなぜこれで干渉するのかイメージできませんでした。
解説
もう一度単スリットの回折条件を示します。
-
- 単スリットの干渉条件
- $d\sin\theta = m\lambda $ 暗線 弱めあう
- $d\sin\theta =m\lambda + \dfrac{\lambda}{2}$ 明線 強めあう( $\theta=0$ のときを含む)

$d$ は単スリットの幅を示すただし $m=\pm 1,\: \pm 2,\: \pm 3,\: \cdots \cdots $
0 を含まず
- 単スリットの干渉条件
暗線の条件
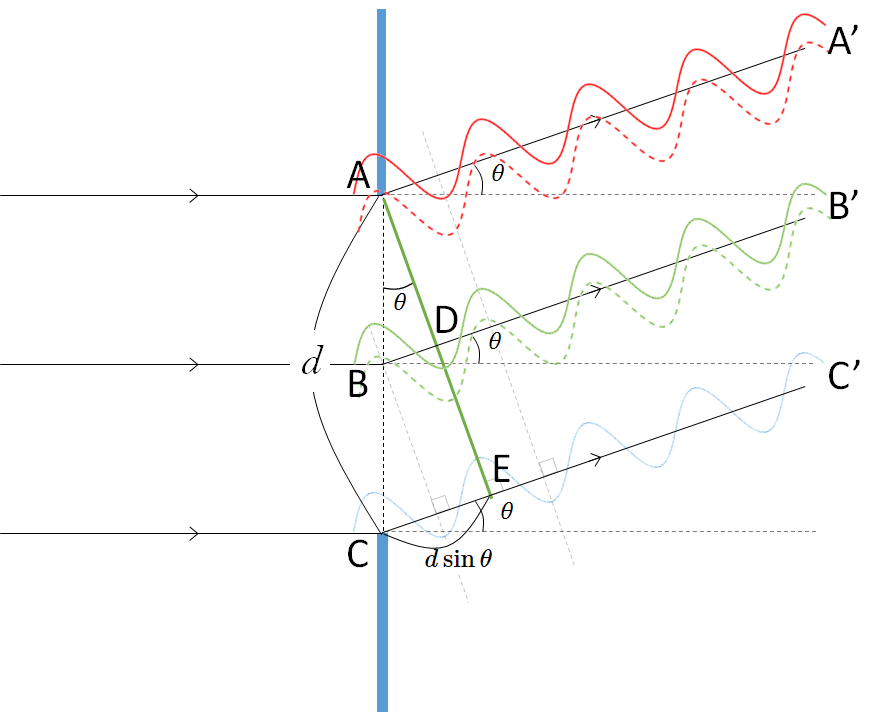
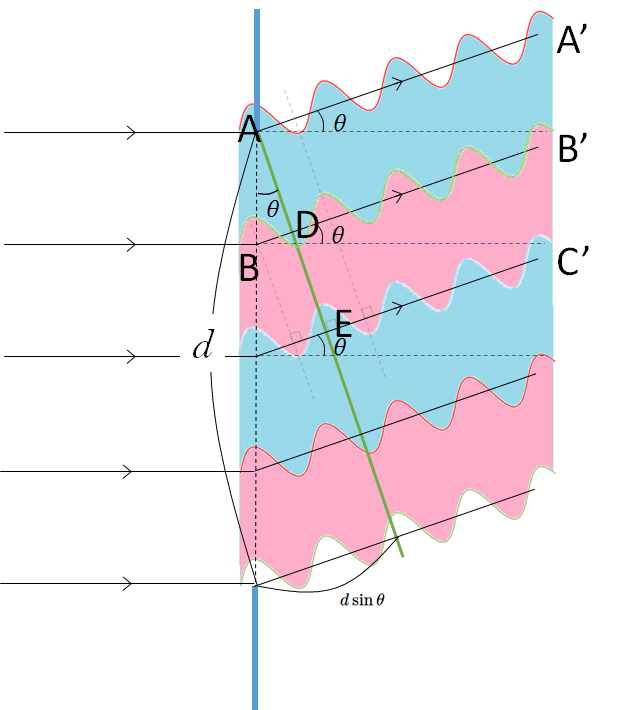
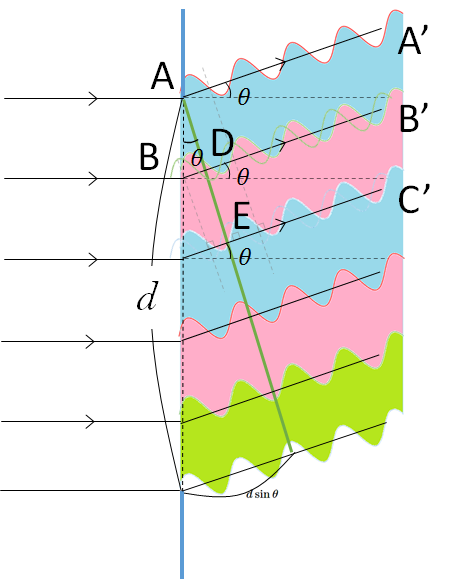
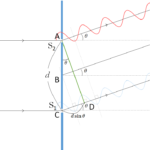
次の図を見てください。
スリット間隔 $d$ で、光の入射方向に対して角度 $\theta$ の方向を考えています。
このとき図の CE の長さが $d\sin\theta=\lambda$ を満たしているときを考えましょう。
波長:$\lambda$
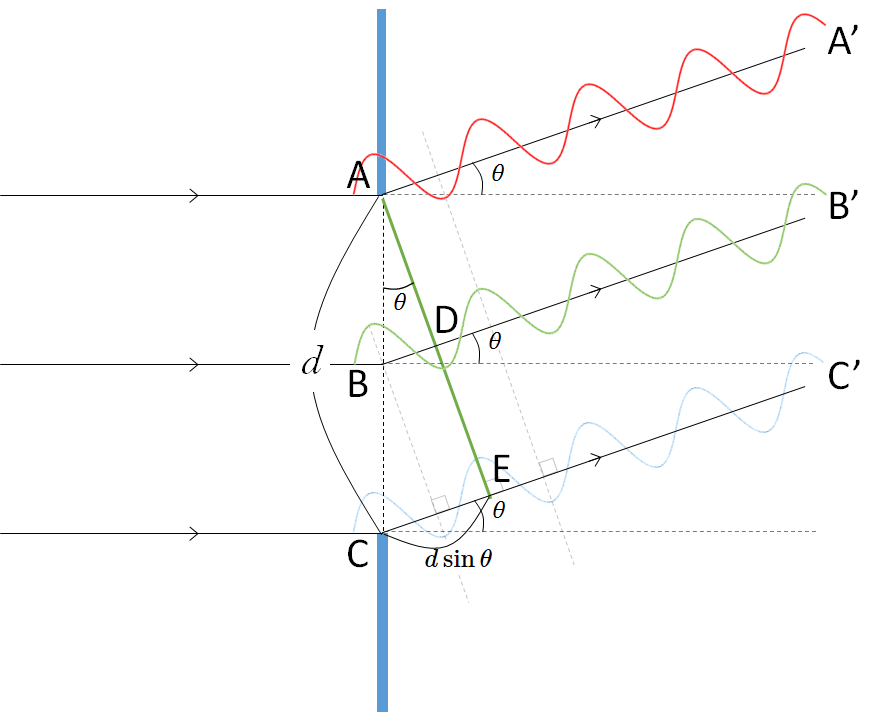
図にあるように、 A と E は同位相で、A と D は逆位相。
したがって、AA’ の波と BB’ の波は打ち消しあうことになります。
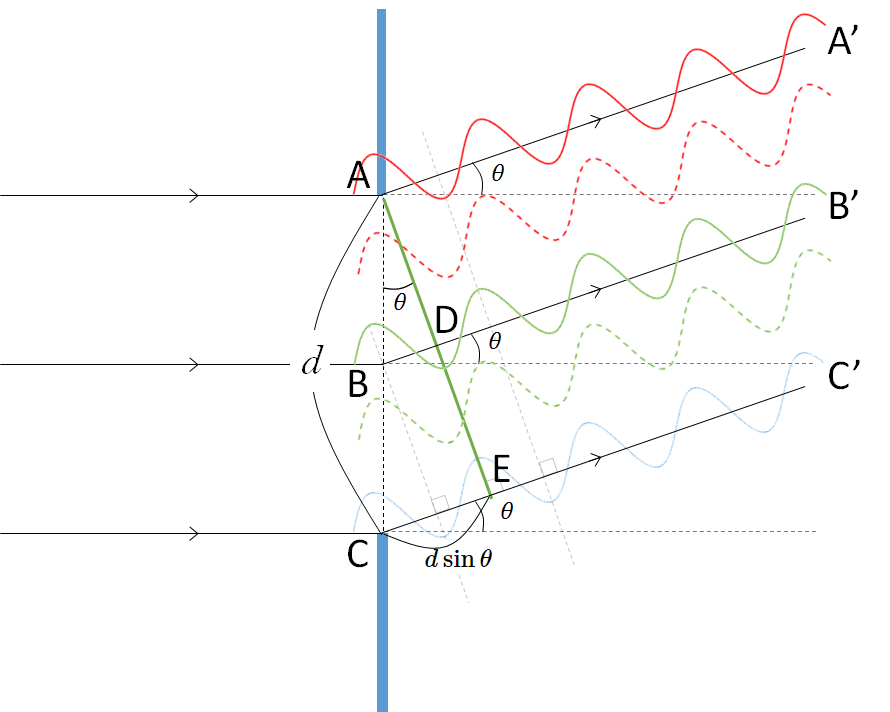
では次の図にあるように、AB の
間にある波(赤の破線)はどうでしょうか?
この波は、図の緑の破線で示される波と打ち消しあいます。
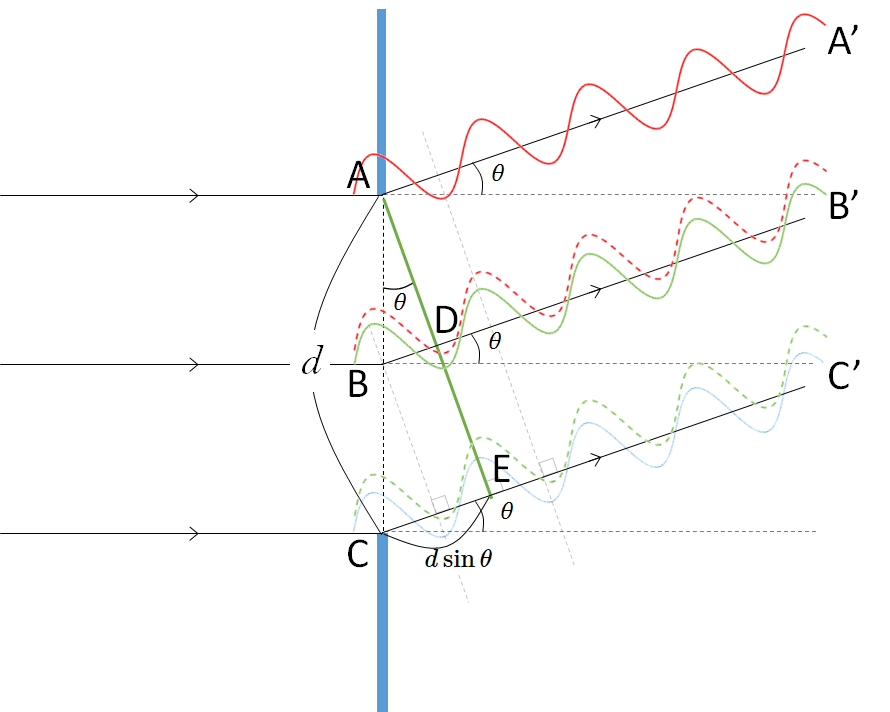
全く同様に、次の緑と赤の破線の波同士も打ち消しあいます。
そしてそれは次の図のように CC’ の波の直前まで同じことが言えるはずです。
次の図でもやはり赤と緑の破線の波が打ち消しあいます。
つまり、この場合、次の図にあるように「青色で示された範囲の波」は「ピンクで示された範囲の波」とちょうど打ち消しあうことになります。
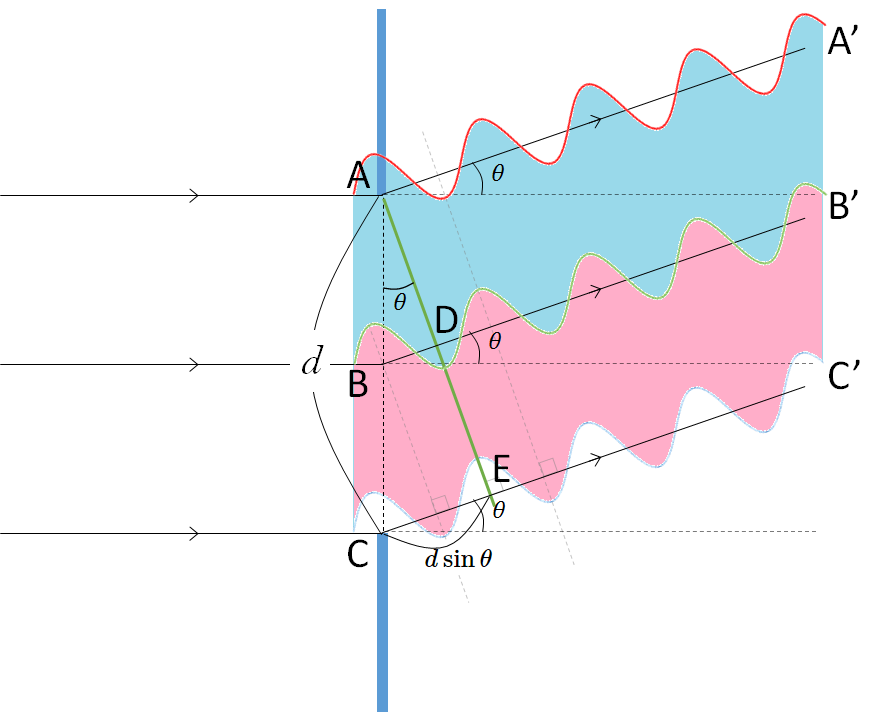
したがって、全体としてこの方向の光は全て打ち消しあうため暗くなるのです。
つまり、
- $d\sin\theta = \lambda $ 暗線 弱めあう
というわけです。
さて、ここで
- $d\sin\theta = m\lambda $
の場合を考えて見ます。
この場合は、図の青色とピンクの範囲で示されるセットがいくつかある、ということと同じです。
この青色とピンクの範囲のセットでちょうど打ち消しあうのですから、いくつこのセットがあってもやはり全体としては暗くなる、ということになります。
したがって、
$d\sin\theta = m\lambda $ 暗線 弱めあう
$m=\pm 1,\: \pm 2,\: \pm 3,\: \cdots \cdots $
0 を含まず
明線の条件
では、先ほどの図に細工をしてみましょう。
BC の後ろに BC と同じ幅を持つ四角形を入れてやります。
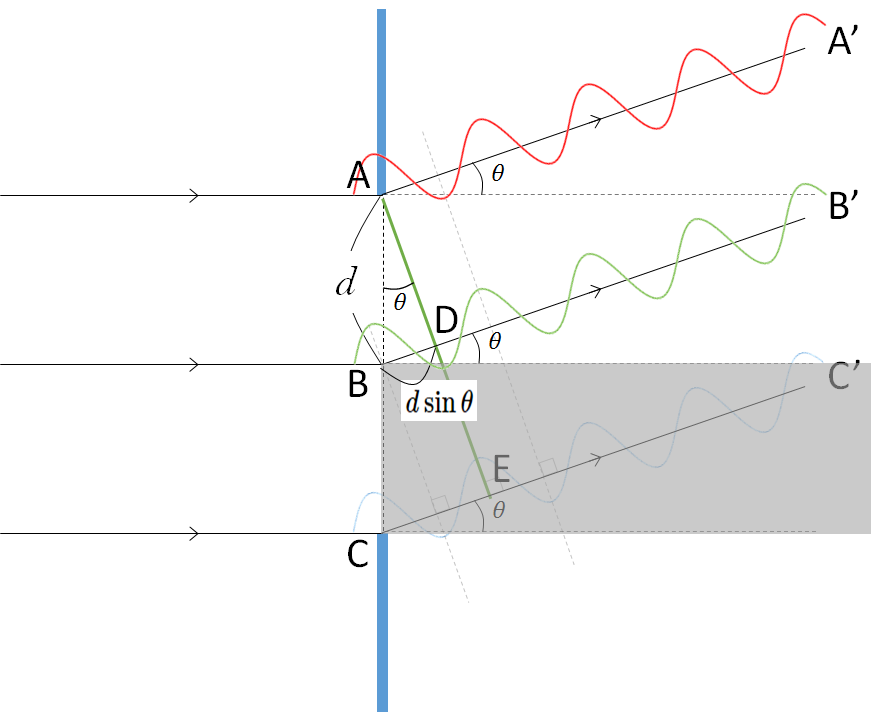
そうすると、スリット幅は AB となりますから、ここで $AB = d$ と書き換えてやりましょう、
その場合、BD の長さは $d\sin\theta$ と書くことができます。
ここで図からわかるように $d\sin\theta= \dfrac{\lambda}{2}$ です。
このとき、先ほど回折した暗条件の場合と同じように考えてみます。
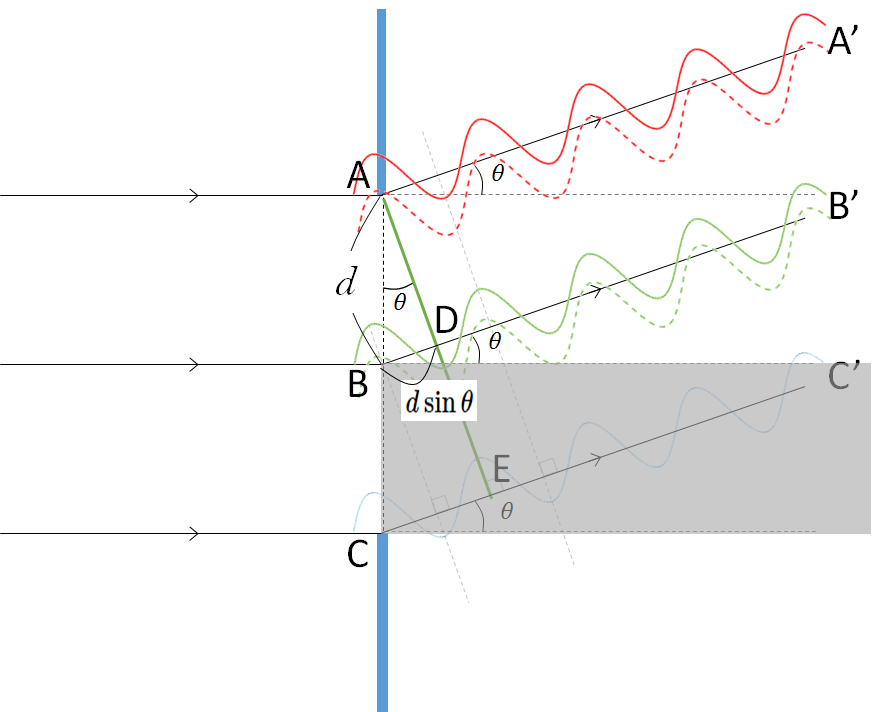
図の赤と緑の破線で示される波は、打ち消しあうはずですが、スリットが狭くなったために、緑の破線の波は出てきません。
したがって、打ち消しあうことがないのです。
つまり、次の図のようにピンクの範囲で示される波がないため、青の波は生き残ることになります。
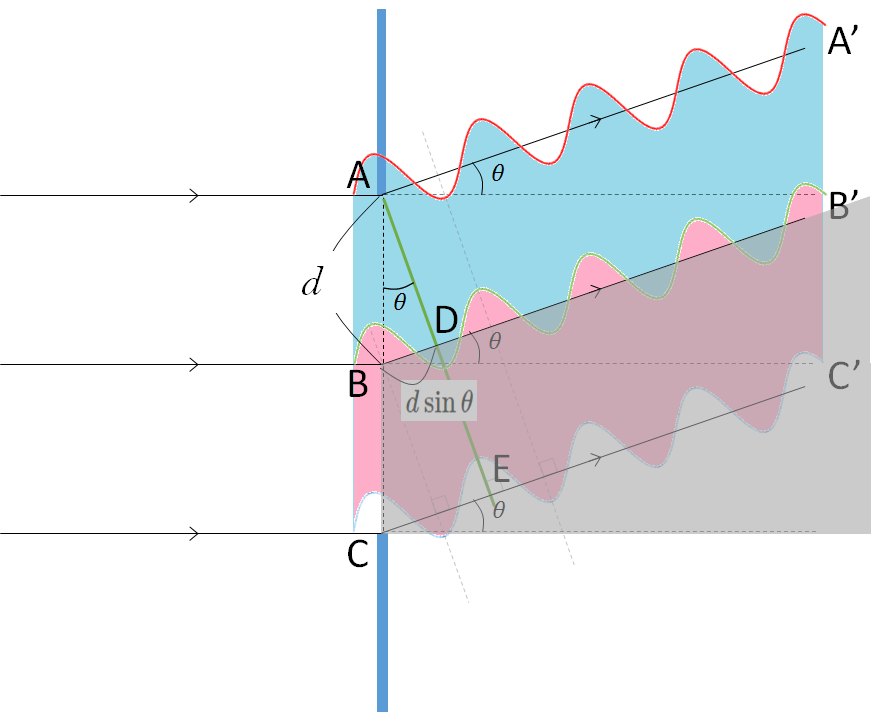
したがって、この場合は、明条件となるわけです。
- $d\sin\theta = \dfrac{\lambda}{2}$ 明線 強めあう
では、 $d\sin\theta =m\lambda + \dfrac{\lambda}{2}$ の場合はどうなるのでしょうか?
このとき $m\lambda$ のセット(青とピンクの範囲)は「暗くなる」という条件でしたから、いくつこのセット(青とピンクの範囲)があっても同じく暗くなります。
しかし、 $d\sin\theta =m\lambda + \dfrac{\lambda}{2}$ では $ \dfrac{\lambda}{2}$ の「オマケ」(図の緑の範囲)が必ずついているわけですから、これは明るくなるはずです。
したがって、
$d\sin\theta =m\lambda + \dfrac{\lambda}{2}$ 明線 強めあう
( $\theta=0$ のときを含む)
$m=\pm 1,\: \pm 2,\: \pm 3,\: \cdots \cdots $
0 を含まず
がいえます。 ただし、$d\sin\theta=0$ は直進光を示しています。
なぜ中心を外れると急激に明るさが失われるのか
なぜ中心を外れると急激に明るさが失われるのか ⇒ それはこの図を見れば明らかでしょう。

$\theta$ が大きくなり、 $d\sin\theta$ に$\lambda$ が多く入れば、上の図のようにほとんどの回折光は打ち消されて急激に暗くなっていきます。
しかし、$\theta$ が小さいうちは図の青とピンクで示される範囲が少ないため緑の明るい部分が目立ちます。




































コメント