$v-t$ グラフを使って考えてみましょう。
物理のエッセンス力学編7番
問題概要
物理のエッセンス力学編6番において、
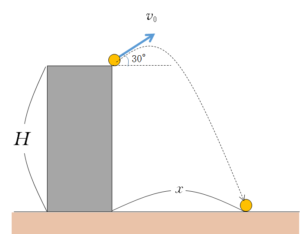
物体を水平から 30° 上向きに初速 $v_0$ で投げ出す場合、最初に地面に落下するまでに飛ぶ水平距離 $x$ を求めよ。
解説
水平投射です。鉛直方向と水平方向に分けて考えます。
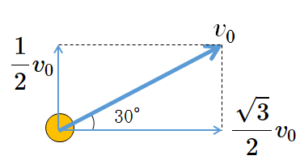
- 鉛直方向の初速度 ・・・ $v_0\sin 30^{\circ}=\dfrac{1}{2}v_0$
- 水平方向の初速度 ・・・ $v_0\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}v_0$
計算式
今回の問題に関しては式を用いて計算したほうがスッキリ・ラクです。
何事も場合による・・・ということでしょうか。
でも $v-t$ グラフの考え方も重要ですよ。
計算
出発点が原点で、変位が $-H$ となることさえわかれば簡単です。
$-H=\dfrac{1}{2}v_0 t -\dfrac{1}{2}gt^2$
より、 $t>0 $ に注意して 解の公式より、
$t=\dfrac{v_0 + \sqrt{v^2_0 + 8gH}}{2g}$
水平方向には $v_0\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}v_0$ で等速運動だから
$x=\dfrac{\sqrt{3}}{2}v_0 \times t$
$t$ を代入して答えを得ます。
答え
$x=\dfrac{\sqrt{3}v_0}{4g} (v_0 + \sqrt{v^2_0 + 8gH})$
$v-t$ グラフでも考えてみます。
こんな考え方もあるのか、という参考にしてください。
他に応用できることもあるでしょう。
$v-t$ グラフ
鉛直方向
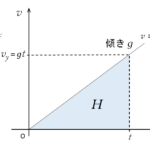
$v-t$ グラフを描いてみます。
鉛直方向には初速度 $\dfrac{1}{2}v_0$ です。
鉛直上向きを正としてみました。
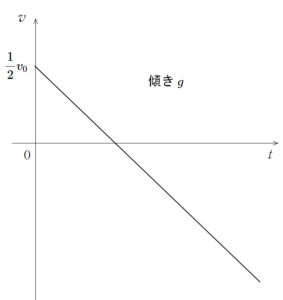
この $v-t$ グラフの傾きの大きさもやはり $g$ です。
そうすると、グラフの傾きが $g$ であるから、投げ出してから最高点に到達するまでにかかる時間 $t_0$ は、
$\mathrm{グラフの傾きの大きさ}=g=\dfrac{\dfrac{1}{2}v_0}{t_0}=\dfrac{v_0}{2t_0}$
$t_0=\dfrac{v_0}{2g}\: \cdots \cdots (1) $
となります。

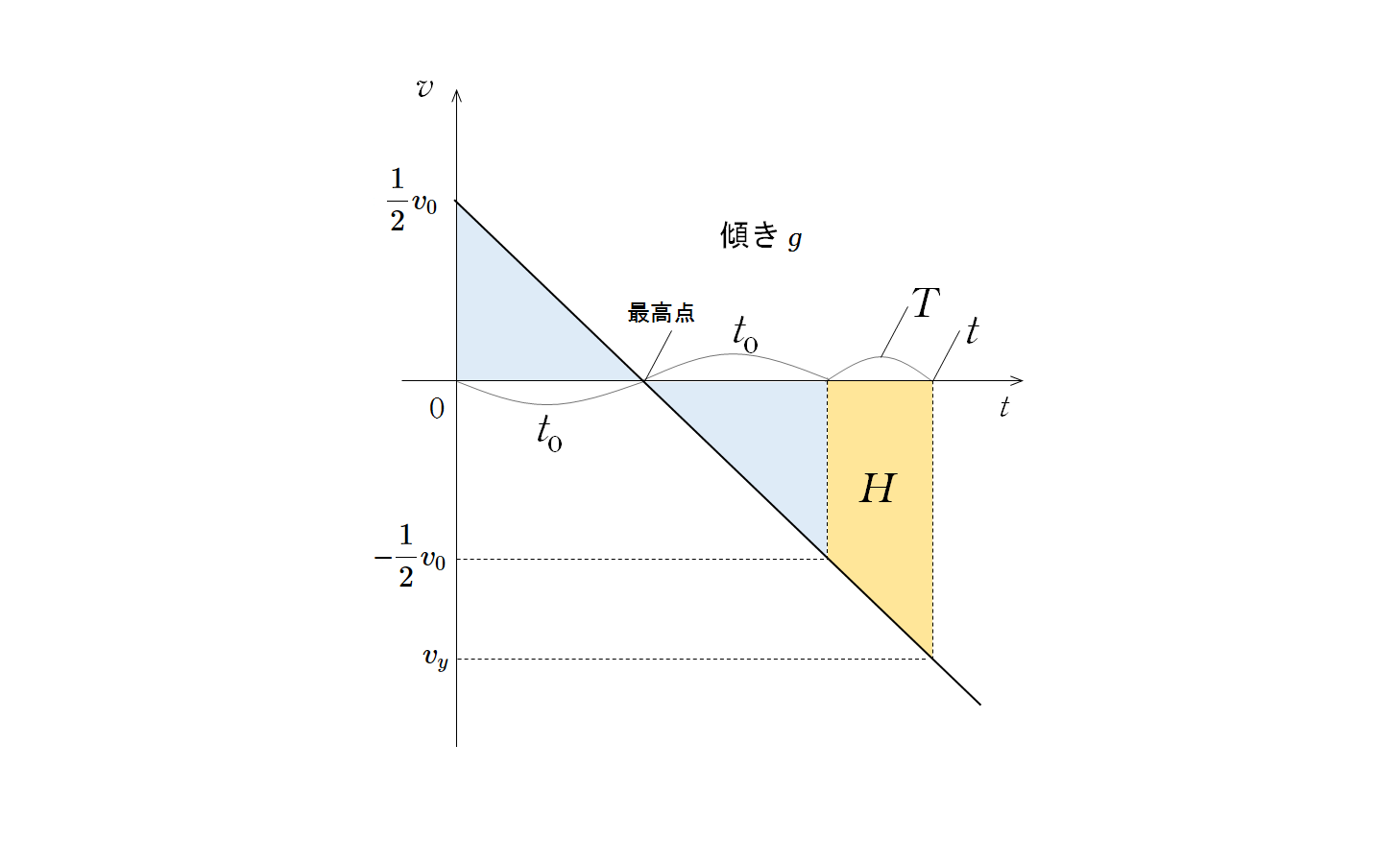
図の水色の三角形は合同です。
三角形の面積は変位を示し、物体が手元に戻るとき変位は 0 になるからです。
したがって、オレンジの台形面積で示される、図の $T$ の時間で落下する距離がビルの高さ $H$ と等しくなっているはずです。
グラフの傾きが $g$ のため、物体が投げ出されてから時間 $t$ たったときの物体の鉛直方向の速度 $v_y$ は $gT$ だけ変化しています。
したがって
$v_y = \dfrac{1}{2}v_0 \: -\: gt < 0$
です。
これらのことから、図のオレンジの時間 $T$ がわかります。
$T=t \:-\: 2t_0=t\:- \: 2\times \dfrac{v_0}{2g} =t \:- \: \dfrac{v_0}{g} $

$(1)$ より、
$t_0=\dfrac{v_0}{2g}$
オレンジの台形の面積を計算します。
$\mathrm{オレンジの台形の面積}=H$
$H=\left \{ \left |-\dfrac{1}{2}v_0 \right | + |v_y| \right \}\times T \times \dfrac{1}{2}$
$~~~~=\left \{\dfrac{1}{2}v_0 +\left (- \dfrac{1}{2}v_0 \: +\: gt \right ) \right \}\times \left (t \:- \: \dfrac{v_0}{g} \right ) \times \dfrac{1}{2}$
これより、
$gt^2-v_0t -2 H=0$
$t>0 $ に注意して、解の公式より、
$t=\dfrac{v_0 + \sqrt{v^2_0 + 8gH}}{2g}$
水平方向
水平方向には $v_x = \dfrac{\sqrt{3}}{2}v_0$ で等速運動しますから、その距離 $x$ は
$x=v_x t=v_0 t$
ここで、 $t=\dfrac{v_0 + \sqrt{v^2_0 + 8gH}}{2g}$ だから、
$x=\left (\dfrac{\sqrt{3}}{2}v_0 \right )\times \left (\dfrac{v_0 + \sqrt{v^2_0 + 8gH}}{2g} \right )$
$~~~=\dfrac{\sqrt{3}v_0}{4g} (v_0 + \sqrt{v^2_0 + 8gH})$
答え $x=\dfrac{\sqrt{3}v_0}{4g} (v_0 + \sqrt{v^2_0 + 8gH})$




































コメント