物理のエッセンス 力学31番
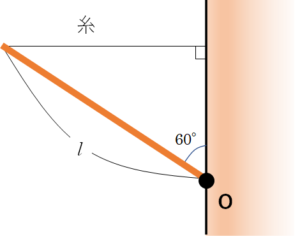
壁にちょうつがいと糸で支えられている棒(図参照)の糸の張力 $T$ と、棒が壁(ちょうつがいをOとする)から受ける力 $F$ の大きさと向きを求める。
解説

ここでもう一度、おさらいしておきましょう。
基本的に剛体の問題の解き方は決まっています。
それは
- 図を描いて、注目物体にはたらく力をすべてかき入れる。← 最重要
- 力のつりあいの式をたてる
- ある点まわりのモーメントの式をたてる ← ある点はどこでもよい
- 以上の式を連立する
です。
多少の違いはあります(手順2・3などの一部が不要なこともあります)が、基本的にはこのようにすればほとんどの問題の糸口はつかめるはずです。
1. 図を描いて、注目物体にはたらく力をすべてかき入れる。
注目物体が受ける力をすべてかき込みましょう。
($T$:張力 $F$ :Oから受ける力 $mg$ : 重力)

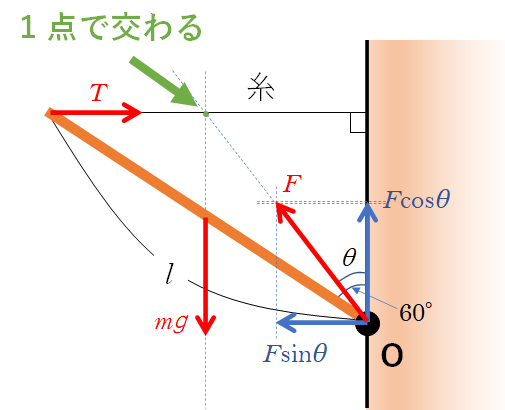
ここで下図のように、棒がちょうつがいを通して壁から受ける力を棒に平行にかいてはいけません。
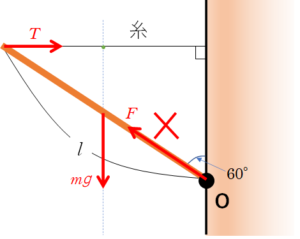
棒は静止しているため、$T$、$F$、$mg$ の力は1点で交わる必要があります。
$F$ を上図のようにかくと、$T$、$F$、$mg$ の力は1点で交わることができません。
このあたりことは次の記事でも解説しています。
ここでは棒に注目しています。棒にはたらく力だけをかくようにしてください。
$T$、$F$、$mg$ の力は1点で交わる必要があるため、次のような図になります。
注:$\theta$ は60°ではありません。
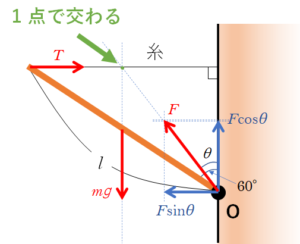

注意:糸は引っ張っているため、糸の張力は糸に沿ってかきます。
これに対して、物体を押したりする場合の力のはたらく方向は状況によります。
2. 力のつりあいの式をたてる
鉛直方向
$F\cos\theta = mg \: \: \cdots \cdots \: 1$
水平方向
$F\sin\theta = T \: \: \cdots \cdots \: 2$
3. ある点まわりのモーメントの式をたてる ← ある点はどこでもよい
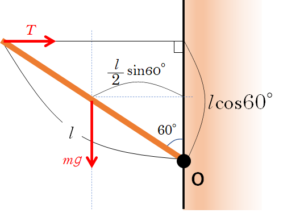
Oまわりモーメントを考えます。

なるべく計算が楽になりそうなところを探しましょう。
Oまわりのモーメントを考えることで $F$ や $\theta$ などが消え、計算が楽になります。
棒は一様であると考えて、重心は棒の中央にあるとします。
したがって、重力のOまわりモーメントは $mg\dfrac{l}{2}\sin 60^{\circ}$ です。
以上のことを踏まえて式をたてましょう。
$T l \cos 60^{\circ}= mg\dfrac{l}{2}\sin 60^{\circ} \: \: \cdots \cdots \: 3$
4. 以上の式を連立する
式 1 と 式2 を辺々割ります、
$\dfrac{\mathrm{式}2}{\mathrm{式}1} = \dfrac{F\sin\theta}{F\cos\theta}=\dfrac{T}{mg}$
よって、
$T=mg\tan\theta$
また、式3 から
$ T = \dfrac{\sqrt{3}}{2}mg $
これらより、
$mg\tan\theta = \dfrac{\sqrt{3}}{2}mg$
したがって、
$ \tan\theta = \dfrac{\sqrt{3}}{2} $
さて、 $F$ の大きさですが、式1と式2から考えます。
$(\mathrm{式}2)^2 + (\mathrm{式}1)^2 = (F\sin\theta)^2+(F\cos\theta)^2 $
こうすることで、$\theta$ が消えます。
よって、
$ F^2=T^2+(mg)^2$
ここへ先ほどの $ T = \dfrac{\sqrt{3}}{2}mg $ を代入します。
$ F^2=\left ( \dfrac{\sqrt{3}}{2}mg \right ) ^2+(mg)^2$
整理して$F$ を得ます。
$F=\dfrac{\sqrt{7}}{2}mg$
動画で解説





































コメント
壁からの垂直抗力Nがある時とないときの違いはなんですか??
この場合も垂直抗力は考えることもできます。
重力のような、何か特別にはたらく垂直抗力という力があるというわけではありません。面から押す力の垂直成分を垂直抗力と称します。
例えば、水平な机の上に置いた物体が受ける垂直抗力の本質的な原因は電磁気力です。