![]() 2022年共通テスト 物理 解説 速報 つくりました!
2022年共通テスト 物理 解説 速報 つくりました!
2021年度大学入学共通テスト物理概要
大学入学共通テスト 2021年度 注目の第1回目です。
![]() 2022年共通テスト 物理 解説 速報 つくりました!
2022年共通テスト 物理 解説 速報 つくりました!
今回は大学入学共通テストについて、解説を行います。
問題概観としては、よく練られた問題で理解力を問うという印象です。
公式暗記・パターン暗記組は苦戦したでしょう。
- 難易度・・・センター試験と比較するとやや難化
- 問題量・・・センター試験と比較すると同じくらい
- 配点・・・・相変わらず1問1問の配点が高く、ちょっとした失敗が大きな失点につながる
- 時間・・・・おそらく足りなかった人が多いのでは?
逆に、物理を根本から理解できている人は、かなり手ごたえを感じた人も多いと思います。
先だって行われた試行テストについてはこの記事で解説しています。
H30年度の試行テストは「思考力」・・というコンセプトにしたがい、センター試験の物理の問題と比較すると難易度が上がっていました。
以前に解説していますが、理解できている人はかなりできる。あやふやな人はかなりできない・・・というように二極化しそうな問題でした。
解説
問題・解答はこちらから
動画解説
第1問
問1
加速運動する台車の問題です。
ここでは、慣性力を考えます。慣性力の大きさは ( $ma$ ) で図の左向きにはたらきます。
したがって、糸は左斜め後方に傾きます。
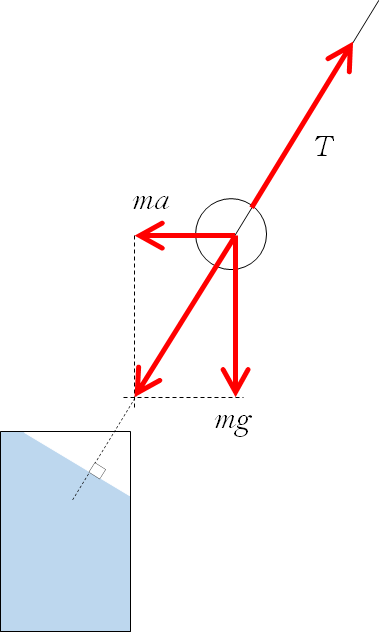
また、慣性力と重力の合力方向が「下」と考えられるため、水面は「下」方向に垂直になります。
したがって、④ 難易度:易
問2
この問題は結構昔からあるオーソドックスな問題です。
誰もが一度は目にしたことがあるでしょうが、初見なら結構苦戦するのではないかな?
いろいろ考え方はありますが、ここは簡単に、「荷物+板+人」を一体と考えみましょう。
図では全体を四角い箱で覆ってブラックボックスにしています。
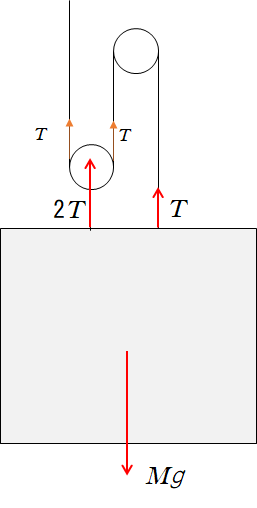
そうすると、このブラックボックスにはたらく力は滑車からの力 $2T$ と、人が引かれる力 $T$ 、そして重力 $Mg$ の3つだけです。
問題によると持ち上げることができたのだから、これらの力はつり合っていると考えられます。
したがって、つり合いの式が成り立ち、
$2T+T=Mg$
ここで、$M$ は「荷物+板+人」の質量だから、$M=50+10+60=120$ kg
ゆえに、
$2T+T=Mg=120\times 9.8$
より、$T=3.9\times 10^2$ N で答えは⑤ 難易度:やや難
問3
静電気力 $F$ は、$F=qE$ として示されます。(電荷 $q$ 電場 $E$)
また、電場 $E=\dfrac{V}{d}$ なので、(極板間距離 $d$ 電位差 $V$)
$F=qE=q\dfrac{V}{d}$
ここで問題より、$q$ と $V$ は一定ですから、$d$ が一番小さいものを選択すればよいことになります。
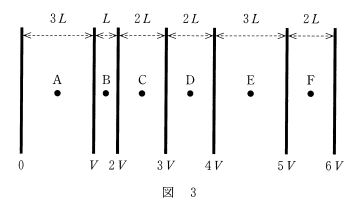
したがって、B の $L$ が一番短いので答えは B の ② 難易度:易
問4
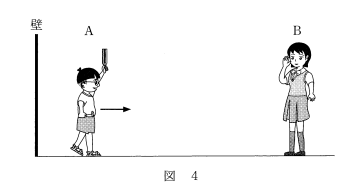
ドップラー効果の問題です。
一般に、音源と観測者が近づくときは、観測される振動数 $f’$ は大きく、遠ざかる時は小さくなります。
さらに、運動する速さが大きいほどその観測される振動数 $f’$ は、より大きく、またはより小さくなります。
うなりの回数 $n$ は、近い振動数 $f_1$ と $f_2$ のとき、 $n=|f_1-f_2|$ 回/s で示されます。
したがって、 ア:大きい イ:小さい ウ:多くなる が正解となります。答えは① 難易度:易
問5
熱力学の問題です。
同じ状態から容器をひっくり返しますが、等温変化と断熱変化の違いを考えます。
最初にグラフの等温変化と断熱変化を見分けます。
等温変化の場合、$pV=k$ ですから、これは数学でよくある $xy=k$ のグラフと同じ形です。
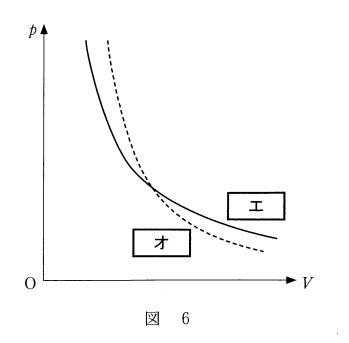
したがって、エが等温変化であるので、オが断熱変化のグラフです。
ちなみに断熱変化の場合は $pV^{\gamma}=k$ になります。($\gamma=\dfrac{C_p}{C_v}$ 比熱比)
次に、ひっくり返した場合のピストンの底面からの距離ですが、まず、図から容器内の圧力を考えます。
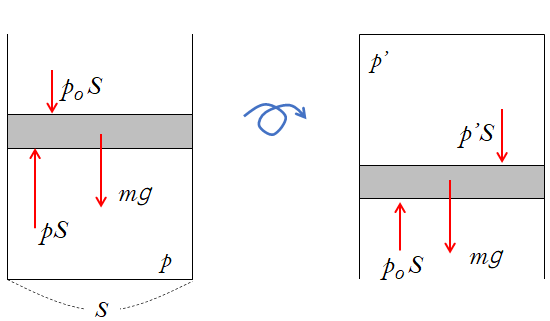
最初の状態での容器内の気体の圧力を $p$ とすると、力のつり合いから、 (ただし、$S$ 断面積 $p_0$ 大気圧 $m$ ピストン質量)
$pS=p_0S+mg$
$p=p_0+\dfrac{mg}{S}$
次にひっくり返した状態の気体圧力を $p^{\prime}$ とします。同様に力のつり合いから
$p^{\prime}S+mg=p_0S$
$p^{\prime}=p_0-\dfrac{mg}{S}$
となり($p>p^{\prime}$)、ひっくり返した方の圧力が(当然ですが)小さくなります。
ここで重要なのは、等温変化でも断熱変化でも最終的には、ひっくり返した場合の圧力はどちらも同じになることです。
となると最初の理想気体の体積を $V$ として
等温変化・・・ $V$ → $V_{等}$
断熱変化・・・ $V$ → $V_{断}$
へと変化したとします。圧力は先ほど考えたように $p$ → $p^{\prime}$ で、ともに同じです。
この変化を先ほどのグラフで考えると、図のように $V_{等}>V_{断}$ が明らかです。
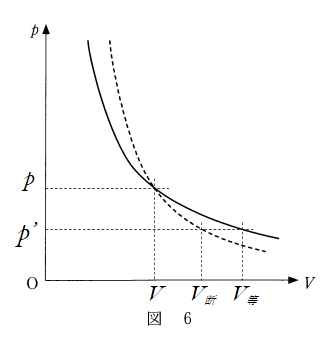
ここで、$V_{等}=S\times L_{等}$ $V_{断}=S\times L_{断}$
なので、結局 $L_{等}>L_{断}$ となります。
まとめると、 エ:等温変化 オ:断熱変化 $L_{等}>L_{断}$ より ② 難易度:普通
長々と書きましたが、グラフが読めれば答えはすぐに出ます。
第2問
問1
$R$ を10 Ω に設定します。
ここで重要なことは、問題文の「スイッチを閉じた瞬間は・・・・」の個所です。
この場合、スイッチを閉じた瞬間ではコンデンサーに電荷がたまっておらず、コンデンサーは導線とみなせます。
したがって、次のような図になるはずですから、6 の答えは ③ 難易度:易
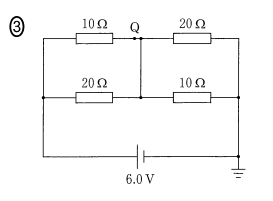
次に、抵抗の配置の対称性から、スイッチを閉じた瞬間に Q を流れる(10 Ω 抵抗を流れる)電流を $i_1$ 、20 Ω 抵抗を流れる電流を $i_2$ としてやります。
まずはオーソドックスにやってみます。
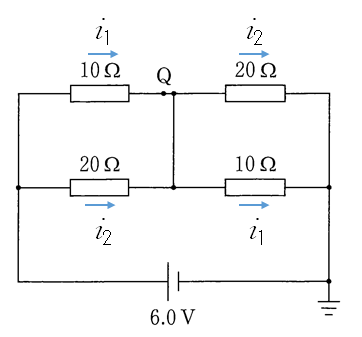
ここでキルヒホッフの法則を用います。
まず、次の左図の黄色で示した閉回路で、 $\sum E=\sum RI$ より
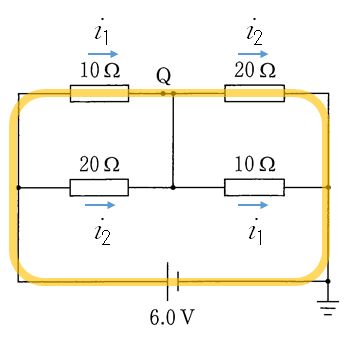
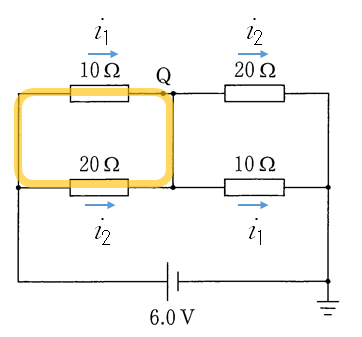
$6.0=10i_1+20i_2$ 次に、図の右の、同じく黄色で示した小さい閉回路を考えると、
$0=10i_1-20i_2$
これら 2 式より、 $i_1=0.30$ A が得られます。
答えは、$3.0\times 10^{-1}$ A となるので
7 の答え ・・・ ③ 8 の答え ・・・ ⓪ 9 の答え ・・・ ① となります。 難易度 普通
別解1
‥‥下のように閉回路を考えればもっと簡単ですね。
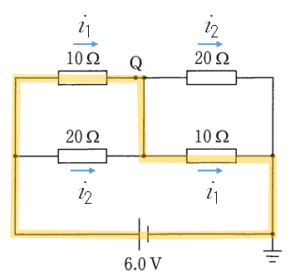
$6.0=10i_1+10i_1$
$i_1=0.30$ A
別解2
回路の対称性から、もう少し簡単に求められる。
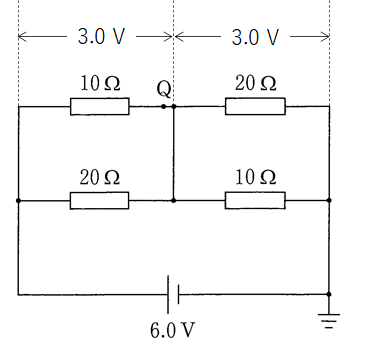
真ん中の導線の左右で対称形になっているため、片方には 6.0 V の半分の 3.0 V ずつかかることになる。(図)
したがって、Q 点の手前の 10 Ω 抵抗には 3.0 V かかっている。
よって、オームの法則から、
$i=\dfrac{3.0}{10}=0.30 $ A
となる。
問2
次に同じ回路において、抵抗は 10 Ω そのままで、スイッチを閉じて十分な時間が経過した場合を考えます。
ここで注意するのは、十分な時間が経過した場合のコンデンサーの状態です。
十分な時間が経過した場合のコンデンサーは断線とみなせます。
十分時間が経過した後は、コンデンサーはフルに充電されています。
その状態では、それ以上電荷が入っていかないので電流が流れ込むことがありません。(コンデンサーを示す記号でも、ちゃんと断線させていますね)
したがって、この場合の回路は次の図と同じと考えられます。
図で、点 P を流れる電流を $i$ とします。
そうすると対称性から、各抵抗を流れる電流は $\frac{1}{2}$ ずつになります。
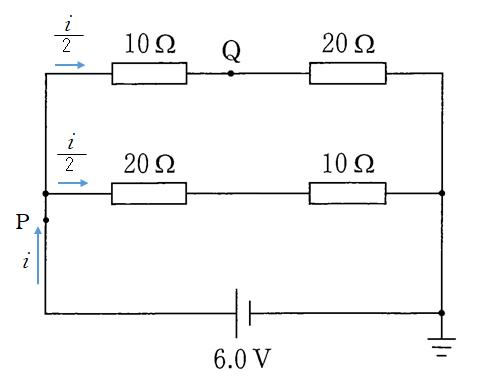
ここでキルヒホッフの法則を適用します。 $\sum E=\sum RI$ ですから、
$6.0=10\times \dfrac{i}{2}+20\times \dfrac{i}{2}$
これより、$i=0.40$ A となります。したがって、10の答え ・・・ ④ 難易度:普通
次に、十分時間経過後のコンデンサーにたくわえられている電気量 $Q$ を求めます。
$Q=CV$ ですから、コンデンサーの極板間電位差 $V$ がわかればよいことになります。
図より、アースの 0 V 点からの電位をそれぞれ $V_1$、$V_2$ とすると、
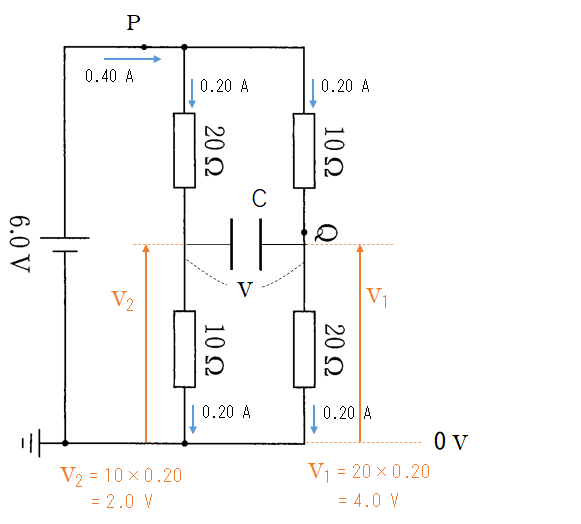
$V_1=20\times 0.20=4.0$ V
$V_2=10\times 0.20=2.0$ V
であるので、コンデンサーの極板間の電位差は $4.0-2.0=2.0$ V です。
よって、コンデンサーにたくわえられている電気量 $Q$ は
$Q=CV=0.10\times 2.0=0.20$ C
となり、11の答えは 0.20 C で・・・② 難易度:普通
問3
次に、コンデンサーにたくわえられている電荷を開放して初期状態に戻します。
そして、抵抗を未知のものに変えます。
キーポイントは「その後、点 P を流れる電流はスイッチを入れた直後の値を保持した。」の部分で、これからこの回路では、「コンデンサーには電荷がたまらない」、「コンデンサーには電流が一切流れなかった」・・・ということがわかります。
よって、コンデンサーの極板間の電位差は常に 0 です。
この場合、たとえコンデンサーの部分を導線に置き換えても、その部分(ブリッジ部分)に電流は流れません。
つまりこの場合、この回路はいわゆるホイートストンブリッジとなっています。
ホイートストンブリッジの式は図のように掛け算で示すと、
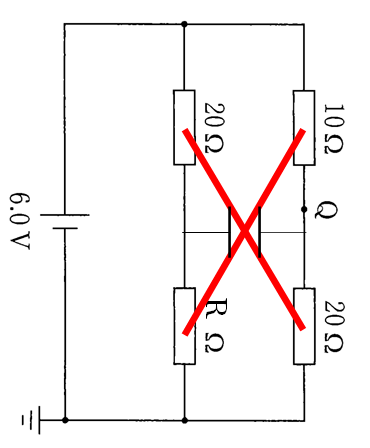
$20\times 20=10 \times R$
より、$R=40$ Ω となり、答えは $4.0\times 10^{1}$ Ω となるので
12 ・・・ ④ 13 ・・・ ⓪ 14 ・・・ ① 難易度:普通
問4
図で導体棒 a が速さ $v_0$ で図の右方向に動き出した直後の電流の流れる方向について考えます。
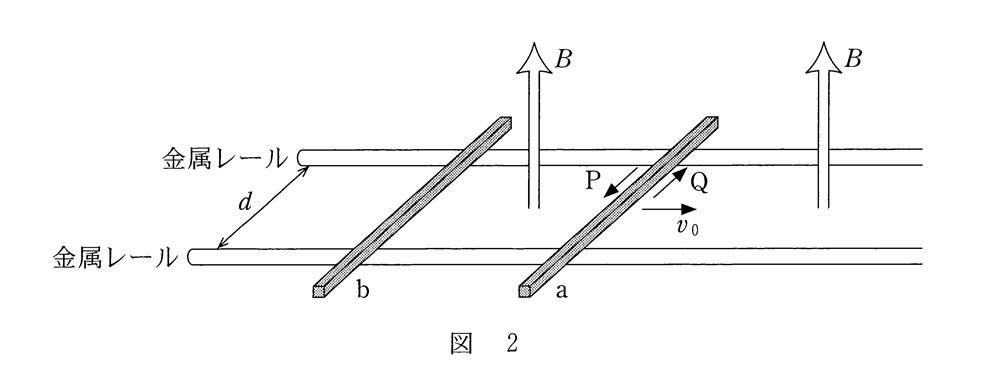
レンツの法則で考えると、導体棒 a が動き出した直後、導体棒 a b と金属レールで作る閉回路を貫く磁束 $B$ は時間とともに増加します。
したがって、閉回路には下向きの磁束を作るような誘導電流が流れます。
(これは導体棒 a の内部の自由電子にはたらくローレンツ力を考えてもOKです)
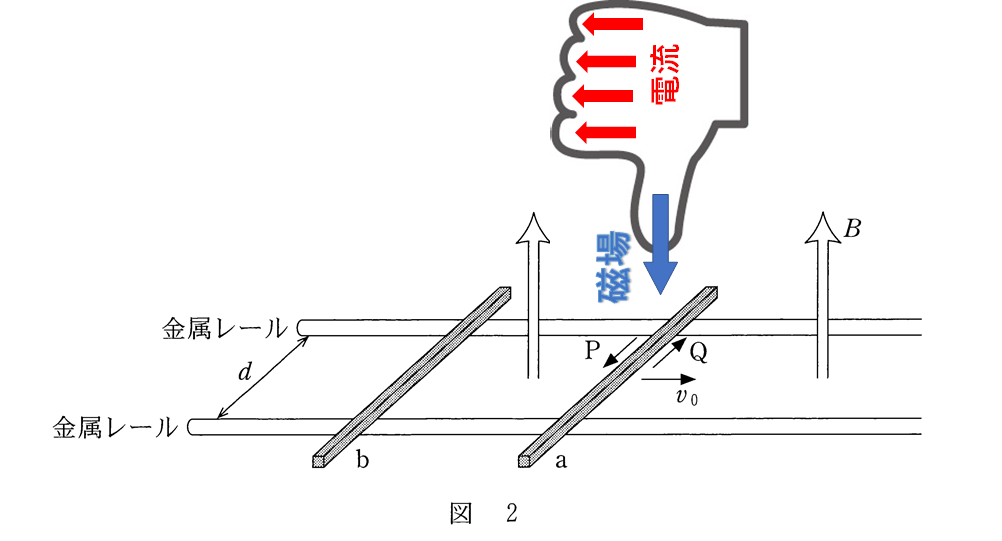
上図のように右手の規則で、図の P の方向に電流が流れることがわかります。
また、その時の回路を流れる誘導電流 $i$ の大きさですが、 オームの法則 $I=\dfrac{V}{R}$ より考えます。
ここで、導体棒 a に生じる誘導起電力 $V$ は、$V=vBl$(起電力はバーベル)より、 $V=v_0 B d$ です。
この時の回路の抵抗 $R$ は、問題から導体棒の単位長さ当たりの抵抗が $r$ で、$d$ の長さのものが二つありますから、 $R=rd+rd=2rd$ となり、したがって、
$i=\dfrac{v_0Bd}{2dr}=\dfrac{Bv_0}{2r}$
です。これより ア:P イ:$\dfrac{Bv_0}{2r}$ ですから、15の答えは ・・・ ② です。 難易度:易
問5
次に導体棒 a が動き始めると、導体棒 b も動き出します。
これは導体棒 a が起電力を発生し、回路に誘導電流が流れるため、導体棒 a b ともにフレミングの力を受けるからです。
このとき、導体棒を流れる電流は次の図で示され、フレミングの左手則で示される力の方向は導体棒 a と b についてそれぞれ赤い矢印のようになります。
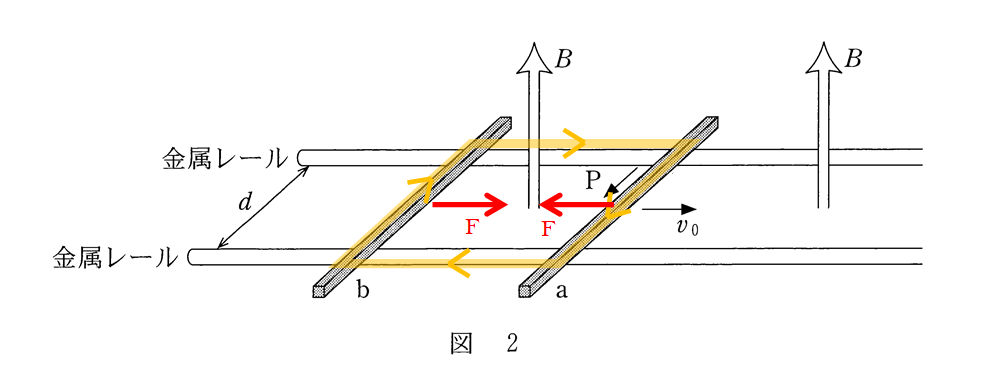
ここで、導体棒 a b に流れる電流は同一で、フレミングの力 $F$ は $F=IBl$ で示されことから、導体棒 a b にかかる力は同じ大きさであることがわかります。
したがって、答えは ③ の「力の大きさは等しく、向きは反対である。」です。 難易度:易
問6
導体棒 a b はともに右向きに運動し、やがて同じ速度になります。
そうなると、金属レールと導体棒のつくる閉回路は面積を増減しませんので、レンツの法則により回路には電流が流れなくなります。
その場合導体棒 a b にはフレミングの力は発生せず、さらに金属レールと導体棒の間には摩擦がないため、慣性の法則により、導体棒 a b はそのまま等速運動を続けます。
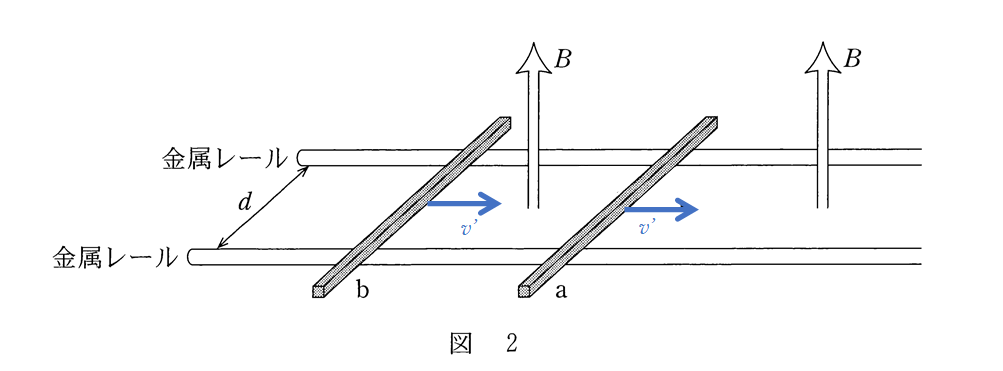
さて、そこに至るまでの間、導体棒 a b は回路を形成してお互いに一直線上反対向きの同じ大きさの力を受け続けます。
回路全体を系と考えた場合、これらの力は内力となり、水平方向には外部から力を受けませんので、系全体で運動量が保存されます。
したがって、系の運動量保存則が成立し、 最初の運動量総和=最後の運動量総和 より、
$0+mv_0=mv’+mv’$
です。よって、 $v’=\dfrac{v_0}{2}$ となります。
導体棒 b は右方向に運動することがわかっていますから、グラフは ③ が正解となります。 難易度:やや難
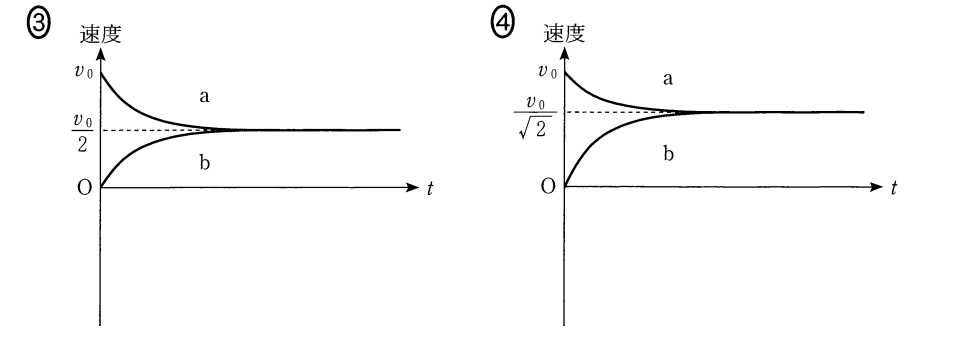
別解
ちなみに、答えを出すだけなら、見ただけで ③ とわかります。
なぜなら、導体棒 b の運動方向から、答えはまず ③ か ④ と考えられますが、 導体棒 a b は質量が同じで、しかも同じ大きさの力を受けて運動するのですからその瞬間瞬間の加速度の大きさは等しいはずです。
④ のグラフの $v-t$ グラフの傾き(これは加速度を示す)の大きさが 導体棒 a と導体棒 b で違っているので ④ は間違いだとわかります。
注意
最初の運動エネルギー $\dfrac{1}{2}mv_o^2$ が保存されるとして、エネルギー保存法則を用いて解くのは間違いです。
回路に電流が流れ、抵抗でエネルギーが熱として散逸するため、力学的エネルギーは保存されません。
この間違いを犯しても、グラフの形から④がおかしいと気がつくはず。
第3問
問1
光の速さは物質中では遅くなります。
その場合、光の波長は物質の屈折率に応じて変化します($\lambda ^{\prime}=\dfrac{\lambda}{n}$)が、振動数は不変です。
したがって、ア:振動数 イ:波長
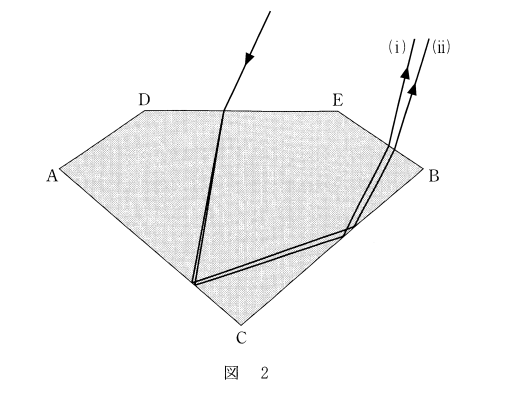
この問題では波長の短い光(屈折率の大きい光)の経路について聞いています。
したがって、 (i) と (ii) の経路で屈折の際によく曲がっている方が正解になります。
よって、(i) が正解です。
まとめると、 ア:振動数 イ:波長 ウ:(i) なので 18 の答えは ・・・ ① 難易度:易
問2
スネルの式を使います。
このとき、よくあるように割り算を使うより掛け算を使いましょう。こちらを参考に。
下の図では、$1\times \sin i =n\times \sin r$ です。こうすると、間違いが少なくなりおススメです。
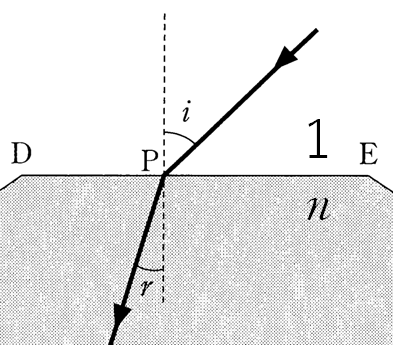
全反射する場合も同じように式を作ります。今度は屈折角が $90$° というだけです。
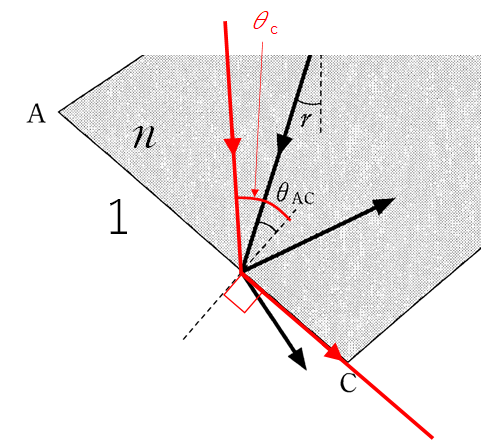
$n \times \sin \theta_c=1 \times \sin 90$°
より、$\sin \theta_c=\dfrac{1}{n}$
まとめると、
$1\times \sin i =n\times \sin r$ と $\sin \theta_c=\dfrac{1}{n}$
よって 19 の答えは ・・・ ② 難易度:易
問3
ダイヤモンドがガラスよりも輝く理由についてです。
その理由は、一言でいうと、ダイヤモンドの屈折率が並外れて大きいためです。
ちなみに、WikiPedia より
| 物質 | 屈折率 | 備考 |
|---|---|---|
| 空気 | 1.000292 | 0℃、1気圧 |
| 二酸化炭素 | 1.000450 | |
| 氷 | 1.309 | 0℃ |
| 水 | 1.3334 | 20℃ |
| エタノール | 1.3618 | |
| パラフィン油 | 1.48 | |
| ポリメタクリル酸メチル | 1.491 | 20℃ |
| 水晶 | 1.5443 | 18℃ |
| 光学ガラス | 1.43 – 2.14 | |
| サファイア | 1.762 – 1.770 | |
| ダイヤモンド | 2.417 |
このためダイヤモンドに入射した光は内部で全反射し、輝いて見えるというわけです。
(ちなみにモアッサナイトは 約 2.6 とさらに大きい値を示します)
問題に戻りましょう。図を見て考えます。

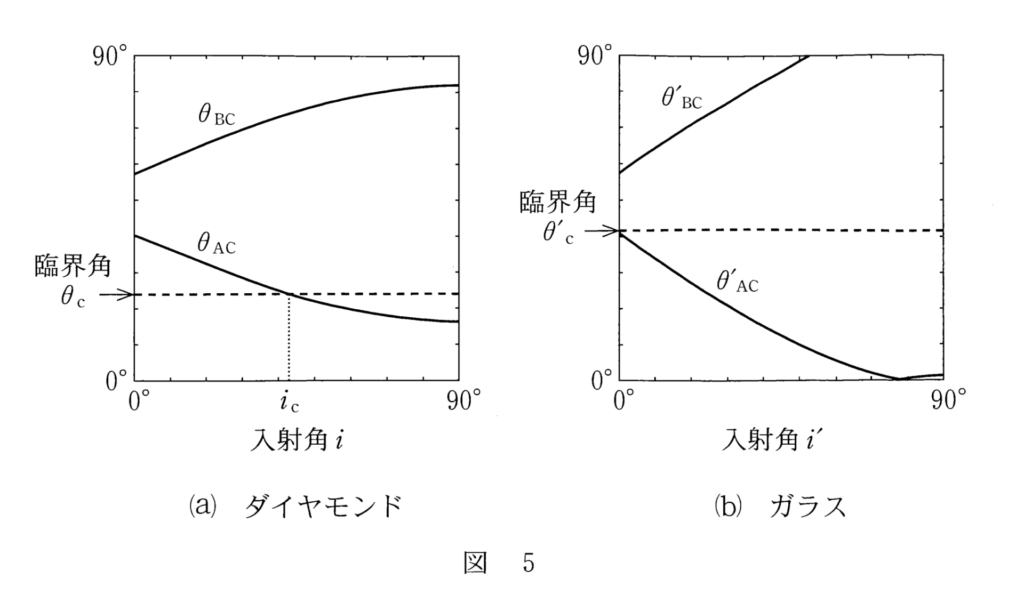
図の (a) では DE 面での入射角が $i_c$ の時、AC面で臨界角 $\theta_c$ になっています。
ここで、 $i$ は DE 面への入射角を示していることに注意します。

この図からもわかるようにAC面へ臨界角 $\theta_c$ よりも大きい角度で入射するときはすべて全反射になります。
図のグラフの (a) では $0^\circ < i < i_c$ の時には $\theta_{AC}$ はすべて $\theta_{AC}>\theta_c$ ですから、全反射することがわかります。
また、$i_c < i < 90^\circ$ の時には $\theta_{AC}$ はすべて $\theta_{AC}<\theta_c$ ですから、部分反射します。
したがって、カ:全反射 キ:部分反射 となります。
次に、ガラスの AC 面への入射を考えます。図 (b)
図の (b) では DE 面での入射角が $i ^{\prime}$ の時、AC面では $0^\circ<i ^{\prime}<90^\circ$ においてすべて臨界角 $\theta_c ^{\prime}$ を下回っています。( $i$ は DE 面への入射角を示していることに注意します)
ということはこの場合はすべて部分反射するということになります。
まとめると
カ:全反射 キ:部分反射 ク:部分反射
となりますから20の答えは、④ 難易度:普通 難しくはないのですが混乱しそうですね。
また、以上から 21 の答えについて、
ダイヤモンドがガラスより明るく輝くのは、ダイヤモンドはガラスより屈折率が「大きい」ため、臨界角が小さく、入射角の広い範囲で二度「全反射」し、・・・・・
となる。 よって、21 の答えは ・・・ ① 難易度:易
グラフから
以上について、グラフで色分けすると次のようになる。
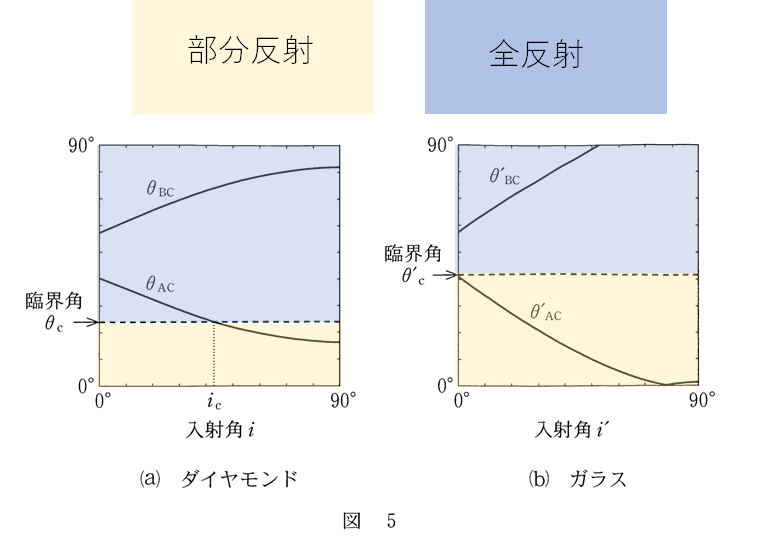
問4
蛍光灯が光る仕組みについてです。
電子が電圧 $V$ で加速された時の電子運動エネルギーを求めます。$W=eV$ より
$eV=\dfrac{1}{2}mv^2=K$
よって $eV$ です。22の答えは ・・・ ② 難易度:易
問5
過程 (a) と(b) で運動量の和について考えます。
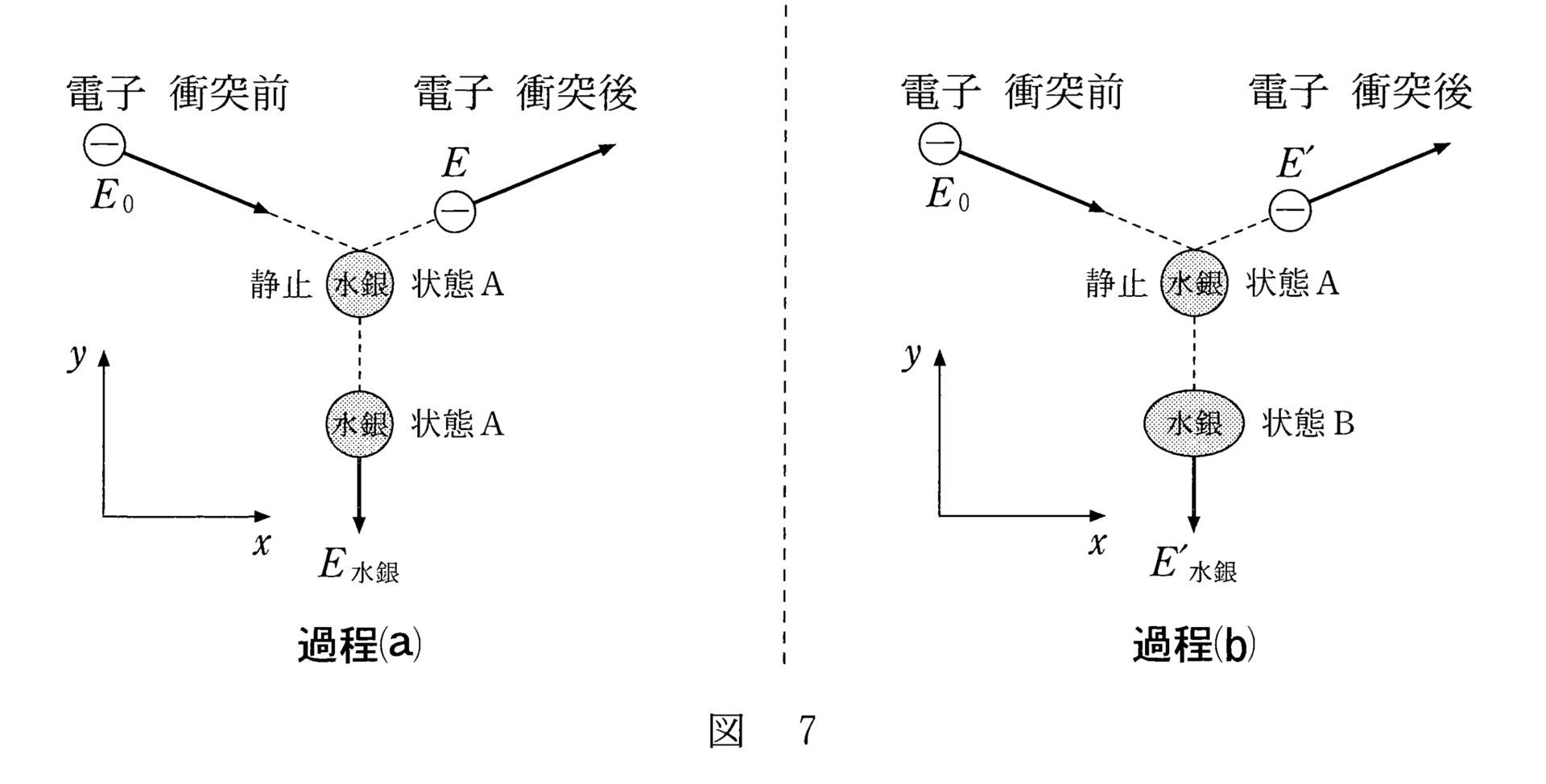
これらの電子と水銀原子全体を一つの系として考えるとき、外力が作用していないため、(a) (b) ともに運動量は保存しています。
23 の答えは ・・・ ① 難易度:易
問6
それぞれの過程において、電子と水銀原子の運動エネルギーの和について考えます。(注意:エネルギー総和ではなく運動エネルギーの和について考えます)
過程 (b) については、電子衝突後の水銀原子がエネルギーの高い状態(励起状態)になっているため、電子の運動エネルギーの一部を受け取っています。したがって、過程 (b) での水銀原子の運動エネルギーは過程 (a) の水銀原子と比べて減少しています。
つまり、(a) の運動エネルギー総和は変化せず、(b) の運動エネルギー総和は減少しているということです。
24 の答えは ・・・ ⑥ 難易度:易
第4問
問1
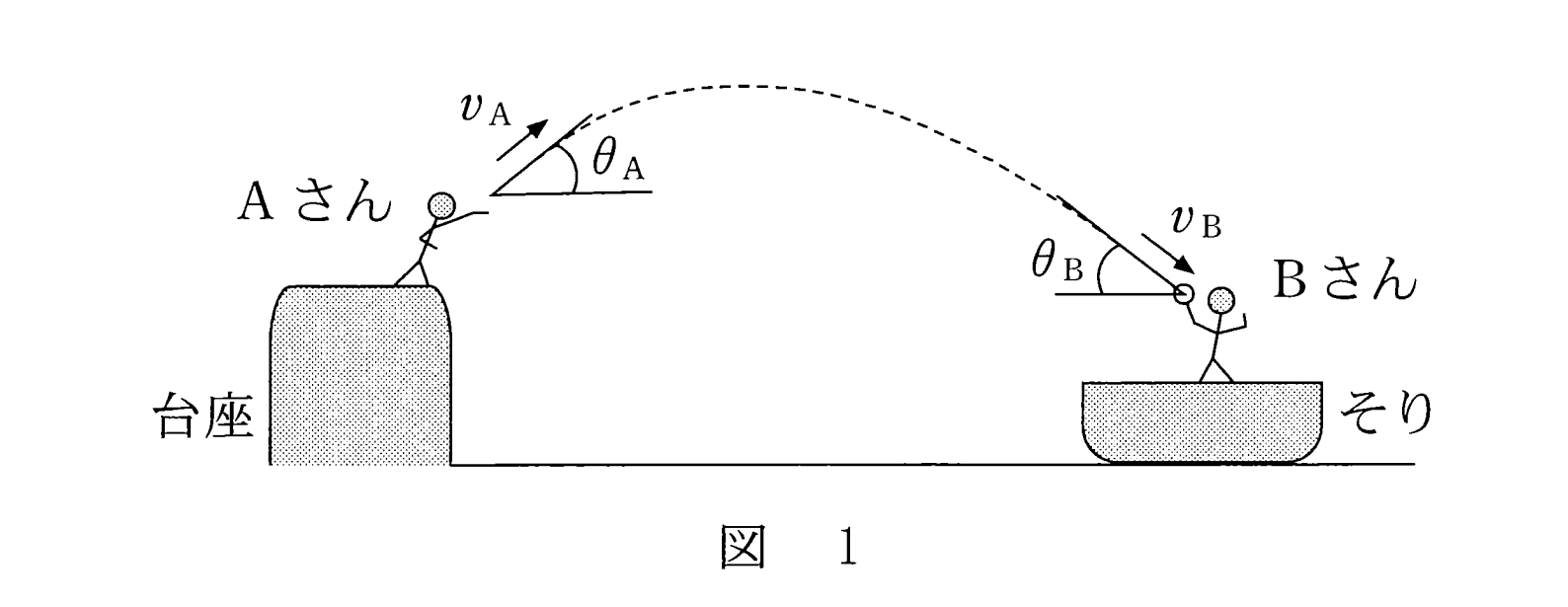
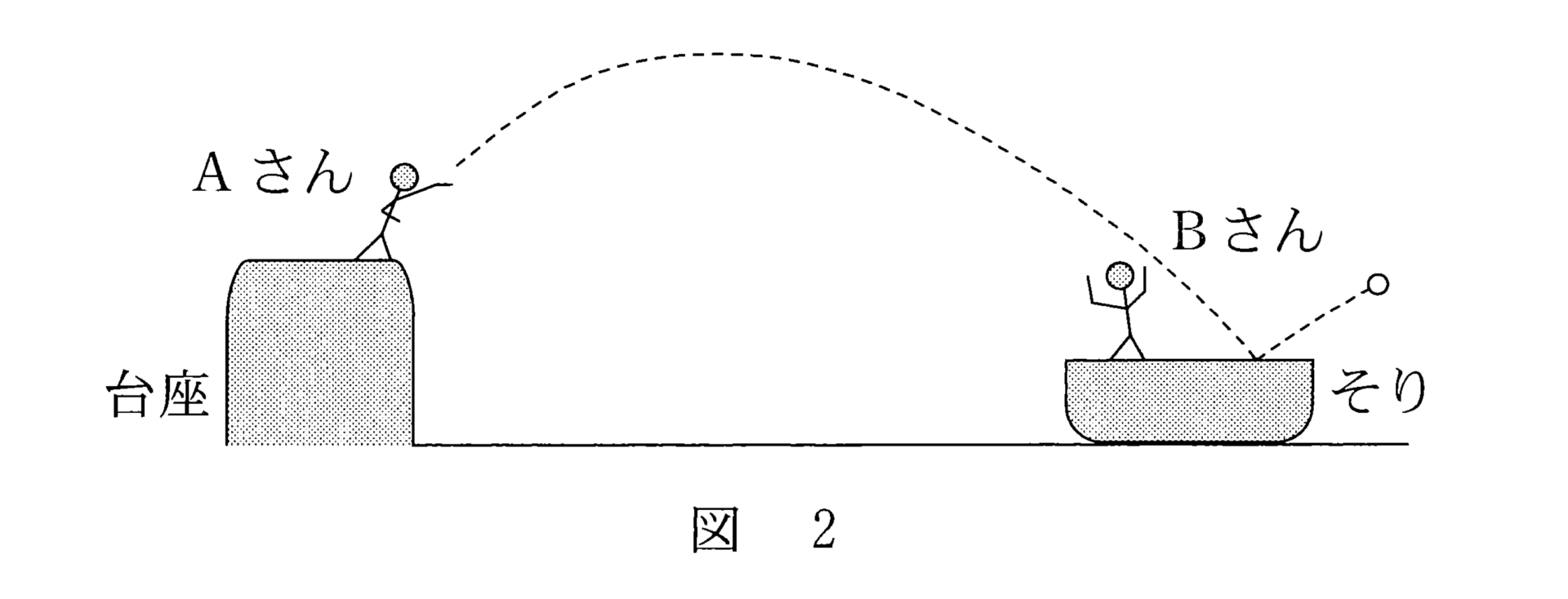
図のように A さんが B さんより高い位置にある時、 A さんの投げたボールの位置エネルギーは B さんが受け取る時のボールの位置エネルギーよりも大きいため、 B さんが受け取るボールの運動エネルギーが増す。よって、 $v_A<v_B$ となります。
また、ボールの速度の水平線分を考えるとき、A の位置でも B の位置でもボールの水平成分の速さは変わらない。
しかし今、 $v_A<v_B$ であるので、誇張して描けば次のようになる。よって $\theta_A < \theta_B$
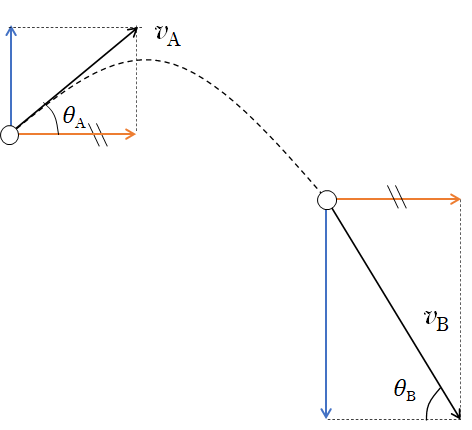
以上より、25 の答えは ・・・ ④ 難易度:易
問2
そりと氷面では、摩擦(外力)がないため水平方向の運動量は保存される。
ここでは、ボールと Bさん、そりを一つの系として考える。
ボールをキャッチする前の運動量総和=ボールをキャッチした後の運動量総和 である。
キャッチ前のボールの水平方向の速度成分は ($v_B\cos\theta_B$) である。
ボールをキャッチ後のそりと B さんの速さを $V$ として、水平方向の運動量保存則より、
$m(v_B\cos\theta_B)=(m+M)V$
これより、 $V=\dfrac{mv_B\cos\theta_B}{m+M}$ となる。したがって 26 の答えは ・・・ ③ 難易度:易
問3
捕球する直前の全力学的エネルギー $E_1$ と、ボールと一体となって等速運動するときの全力学的エネルギー $E_2$ を比較する。
このとき、力学的エネルギーが保存されるとするのは間違いである。
なぜならば、ボールは B さんに捕球されており一体となるため、反発係数が $e=0$ と考えられるからである。
この場合、エネルギーは一部、熱などになって散逸する。
したがって、 $\Delta E=E_2-E_1<0$ となる。
27 の答えは ・・・ ① の「$\Delta E $ は負の値であり、失われたエネルギーは熱などに変換される」が正しい。 難易度:易
問4
Aさん:そりはつるつるの氷の上にあるのに、動かなかったのはなぜ?
それはボールとそりの間に水平方向に力がはたらかなかったから(摩擦がなかった)といえます。
そういった場合、そりはボールがぶつかっても水平方向に力を受けないので運動することはありません。
よって ア:はたらいた力の水平方向の成分がゼロ となります。
次にイ
Aさん:ボールとそりは必ず弾性衝突しているんだろうか?
この場合、必ず弾性衝突している必要はありません。
なぜなら条件を満たすためには、水平方向に力がはたらかなければよいだけなので、鉛直方向の反発係数は 1 である必要はありません(もちろん 1 でもかまいません)。
したがって、 イ:「いいえ、鉛直方向の運動によっては弾性衝突とは限らない」が正解です。
以上より 28 の答えは ・・・ ④ 難易度:易







































コメント