物理基礎概評

大学入学基礎テスト 物理基礎 について解説します。
大学入学共通テスト 2021年度 注目の第1回目です。
- 難易度・・・センター試験と比較すると易しめ
- 問題量・・・センター試験と比較するとやや増
- 配点・・・・1問1問の配点が高く、ちょっとした失敗が大きな失点につながる
- 時間・・・・時間には比較的余裕があったのでは?
旧センター試験と同様やはり「おいしい科目」という印象です。
物理をきちんと理解している人にとっては容易だったのではないでしょうか。
ただ、内容的には平易ですが、現役生は電気分野が後回しになっている人が多く、電磁気の理解度により点数は上下すると思います。
解説
問題はこちらから
第1問
問1
木片にはたらく力を描き入れます。
- 重力
- 床からの力
- りんごからの力
これらはすべて木片が受ける力です。
図で赤は木片が受ける力、青はりんごが受ける力、緑は床が受ける力 です。
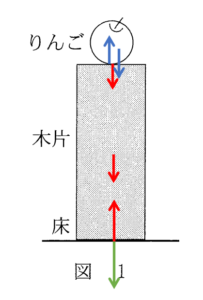
難易度:易
作用反作用などについて正しい知識を
問2
静電気で、正と正 負と負 は反発、正と負 は引き合う・・・ということを知っていれば十分です。
ただし、3 は棒に描かれた矢印の向きを聞いていますのでご注意を。(④と勘違いしそう)
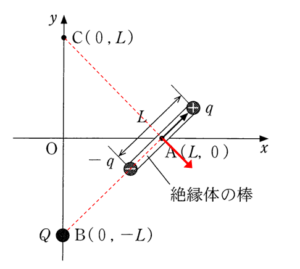
難易度:易
問3
これは知識を問う問題です。以下は常識として覚えておきましょう。
電波 赤外線 可視光線(赤橙黄緑青紫) 紫外線 X線 γ線
波長 長い‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 短い
振動数 小 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 大
エネルギー 小 ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 大
難易度:易
問4
間違い探しです。
② 熱エネルギーになってしまうと、その一部でも仕事に変えられない —>熱を仕事に変える機関はいろいろあります。
⑤ 絶対0度は -273 ℃ ですね。
難易度:易
第2問
問1
グラフから読み取るだけです。波形から1周期の時間を読みましょう。
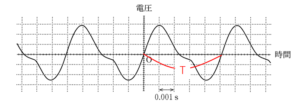
グラフから $T=0.0051$ [s] です。
また、周期がわかったら $f=\dfrac{1}{T}$ から振動数を計算して、表1から適当なものを選択します。
選択肢から選ぶだけなので概算でよいでしょう。
$f=\dfrac{1}{T} \fallingdotseq \dfrac{1}{0.005}=200$ Hz ですから、「ソ」ですね。
難易度:易
問2
実線と点線の波形を合成します。下の図ではいくつかの点(赤丸)をとりました。
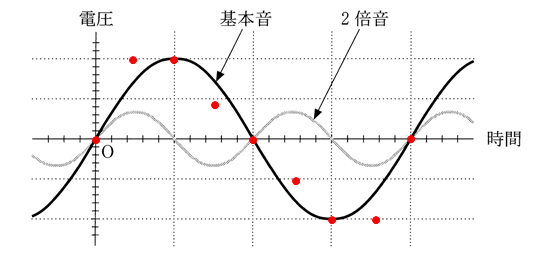
選択肢から選ぶので、だいたいの波形がわかればOKです。
基本音と倍音の合成なので、基本的な合成音の高さは基本音に従います。
よって、基本音を少し崩した形になるため、①と③はない、ということになります。
難易度:易
問3
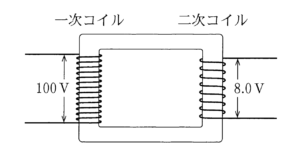
変圧器では次の式に従います。
1 次電圧 $V_1$ 2 次電圧 $V_2$ 1 次の巻き数 $n_1$ 2 次の巻き数 $n_2$
$V_1:V_2=n_1:n_2$
したがって、$100:8.0=n_1:n_2$
より、$n_2=\dfrac{8.0}{100}n_1$
難易度:易
問4
電力は $P=IV$ で示されます。
また、理想的な場合は変圧器内部で電力損失がないため、1 次側の電力 $P_1$ と2 次側の電力 $P_2$ は等しくなります。
ゆえに、
$P_1=I_1V_1=P_2=I_2V_2$
$I_1\times 100 = I_2 \times 8.0$
より、 $I_2=\dfrac{100}{8.0}I_1=12.5I_1$
難易度:易
問5
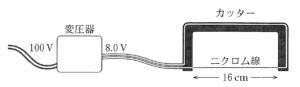
カッターの消費電力 $P$ を求めます。
カッターの抵抗 $R$ は、長さ 1 m あたりの抵抗値が $8.0$ Ω なので、 $R=0.16\times 8.0 $ Ω となります。
消費電力の式 $P=IV=I^2R=\dfrac{V^2}{R}$
よって、 $P=\dfrac{V^2}{R}$ より、
$P=\dfrac{V^2}{R}=\dfrac{8.0^2}{0.16\times 8.0}=50$ W
難易度:易
第3問
問1
図の定規の AB 間の長さは 2.6 cm 。
打点は 6 個あるのでかかった時間 $t$ は、 $t=6\times \dfrac{1}{60}=0.10$ s
よって、 $\overline{v}_{AB}=\dfrac{2.6\times 10^{-2}}{0.10}=0.26$ m/s
難易度:易
問2
$v-t$ グラフの傾きは加速度を示す。
この台車の $v-t$ 図の傾きが一定となっているため、加速度は一定であったことがわかります。
台車を引く力は水平方向(加速度の方向)には張力 $T$ だけであるので、運動方程式から
$F=T=ma=0.50\times 0.72=0.36$ N
難易度:易
問3
この問題は、もちろん「スマートフォンの分だけ全体の質量が大きくなったため」です。
蛇足ですが検証してみましょう。
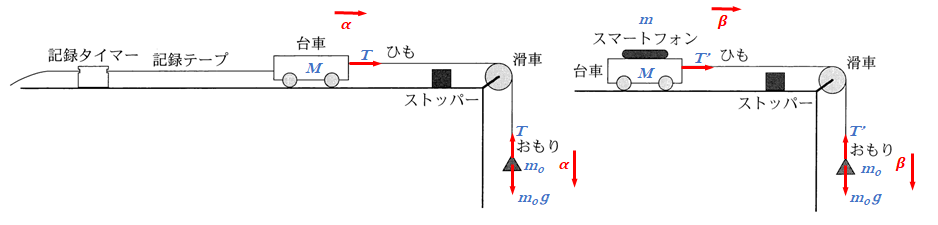
運動方程式を立ててみます。台車の質量 $M$、おもりの質量 $m_0$ とします。
まず、スマートフォンなしの場合、加速度を $\alpha$ 、糸の張力 $T$ とします。
- $M\alpha=T$
- $m_0\alpha=m_0g-T$
これより、$\alpha=\dfrac{m_0g}{M+m_0}$
スマートフォン(質量 $m$)ありの場合、加速度を $\beta$ 、糸の張力 $T’$ とします。
- $(M+m)\beta=T’$
- $m_0\beta=m_0g-T’$
これより、$\beta=\dfrac{m_0g}{M+m+m_0}$ となり、スマートフォンの分だけ全体の質量が大きくなったからだということがわかります。
ついでに、注意です。
よくある勘違いとして、両方の場合で糸の張力が同じだとするものがあります。
このとき、上の方程式から
$T=\dfrac{Mm_0g}{M+m_0}$
$T’=\dfrac{(M+m)m_0g}{M+m+m_0}$
となり(当然ながら)同じではありません。
難易度:易
問4
グラフから等加速度運動している時間を読み取ると、1.7 s 。
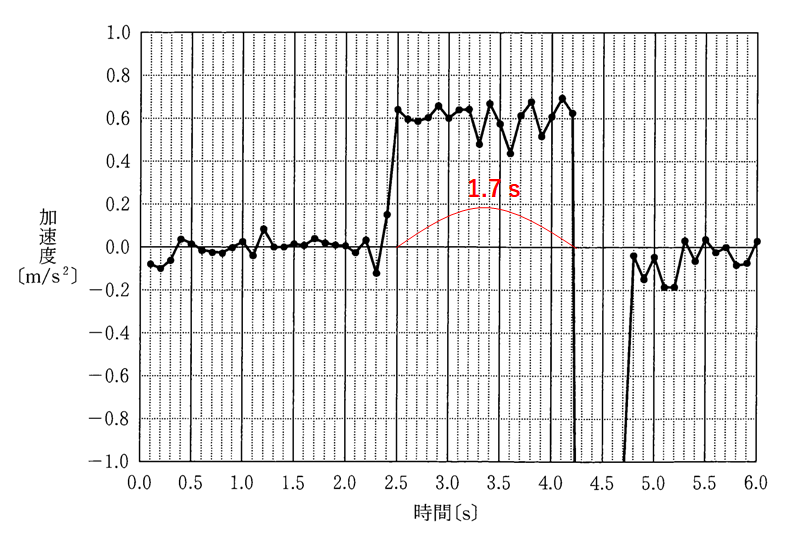
台車の初速度は 0 と考えられるから、加速度を $a$ として、時間 $t$ では
$v_1=at=0.60\times 0.17 \fallingdotseq 1.0$ m/s
です。
難易度:易
問5
台車がを引いているおもりが落下しているとき、おもりのエネルギー変化を考えます。
注意:摩擦がない ・・・ こういう問題だと条件反射的に「力学的エネルギー保存」が出てきて、検討せずに判断してしまいがちです。
結論から言うと、この場合、おもりの持つ力学的エネルギー(位置エネルギー+運動エネルギー)は減少しています。
この場合、摩擦がないので、系(台車、おもり、ひも)としての力学的エネルギーは保存されます。
しかし、今聞かれているのは「おもりのエネルギー」であることに注意します。
おもりにはたらく力を考えてみます。
おもりにはたらく力は 重力 張力 です。
おもりが重力だけを受けて落下している場合を考えると、力学的エネルギーは保存しています。
しかし、この場合、おもりは上向きに糸の張力 $T$ を受けているので、それにより負の仕事($-Th$)をされます。
その結果、おもりの持つ力学的エネルギーは減少しています。
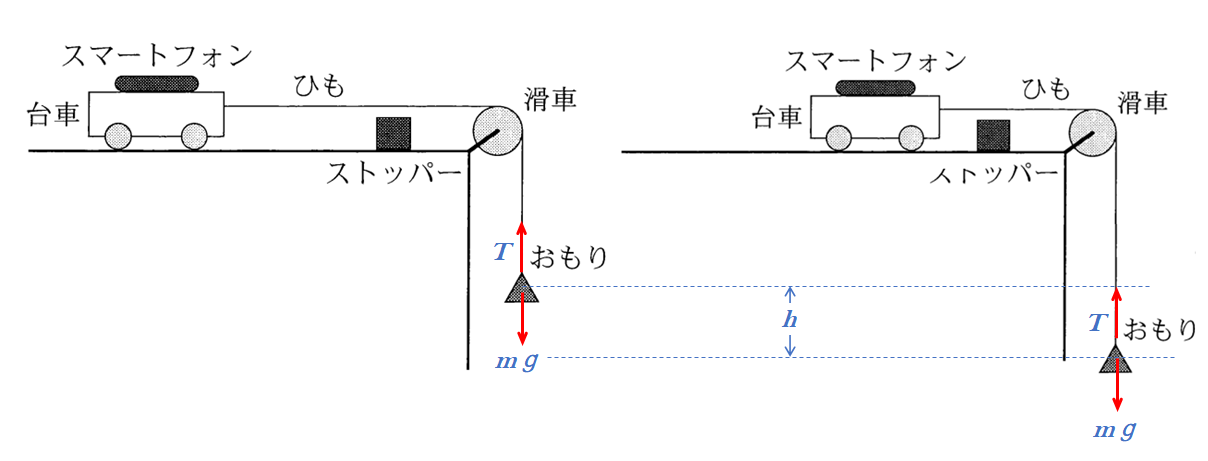
直感的に言えば、糸でつながれていなければ、おもりはもっと速くなりますね。
しかし、糸がおもりを引くためそれほど速くなれない・・・から明らかです。
難易度:易 (引っかかった人がいるかも・・・)






































コメント