回折現象をご存知ですね?
波が障害物の背後にまで回り込む現象。
一般に波長が長いほどその効果が顕著になる。
なぜですか?
なぜ波長により回折の度合いが変化するのでしょうか?

回折とは
回折とは障害物の背後にまで波が回り込むことです。
この現象は日常ありふれています。
例えば、物陰にいても音を聞くことができるのは、この回折現象のためです。
光も波動ですから回折現象を起こします。
しかし日常、光の回折現象を意識することはありません。
これは、光の波長が非常に短いために回折現象が目立たないからなのです。
もし光の回折現象が顕著であるなら私達の世界から影がなくなります。
波の干渉
回折について理解するために波の干渉についておさらいをしておきます。
2つの波源から出た波は互いに干渉し強め合ったり弱め合ったりします。
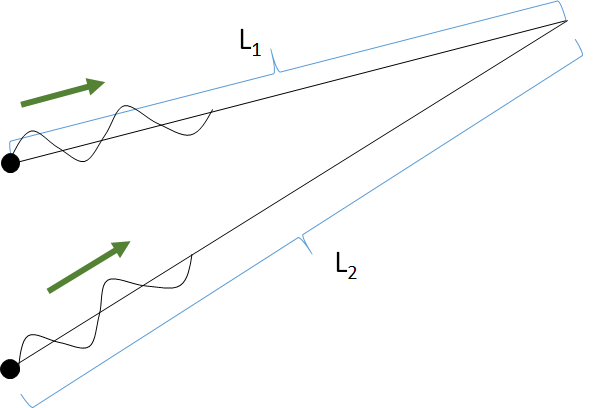
このときある地点の波源からの距離を $L_1$ 、$L_2$ とします。
そうすると2つ波源から波が同位相で出る場合、次のことが言えます(振幅・波長・振動数は同じとします)。
$|L_1-L_2|=m\lambda ・・・強めあう$
$|L_1-L_2|=m\lambda + \dfrac{1}{2}\lambda ・・・弱めあう$
$(m=0,\:1,\:2,\:3,\:4,\: \cdots)$
波長と回折現象
一般に教科書等でよく使われる次の図を考えてみます。
 |
 |
この場合、波長に対して隙間が狭いほうが回折現象がよく現れるということになっています。
でも、なぜだか考えたことはありますか?
教科書にもあまり説明は載っていないように思います。
なぜでしょうか?
ここではこの現象について考えてみます。
回折した波の干渉
波長が隙間に対して長い場合
では次の図を見てみましょう。
この図は、波長が隙間に対して長い場合です。
ホイヘンスの原理により障害物の隙間においては無数の点波源があると考えられます。
このとき、隙間から出た波を考えるとき、障害物の裏側では多数の波が干渉し合います。
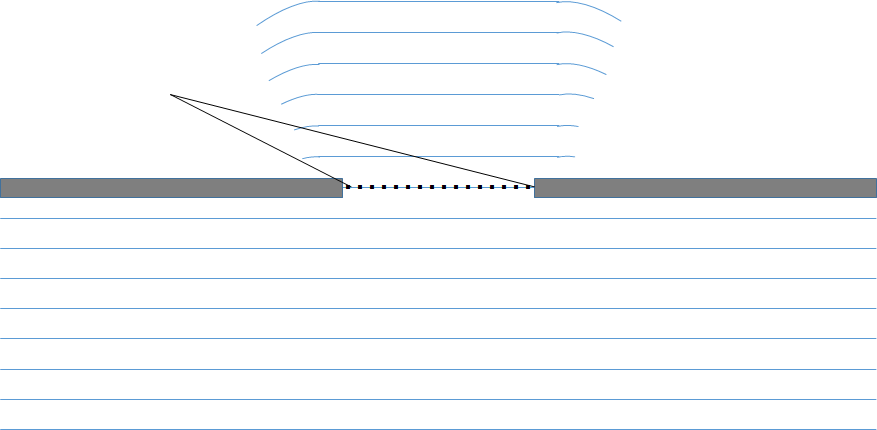
例えば、図のように隙間の端と端から出た波を考えると、それらの波の位相差は大きくなります。
そのため、色々な位相の波が重なり合うことで打ち消し合ってしまうのです。
よって、障害物の裏側まで回折した波の多くは弱めあってしまい観察されなくなるのです。
波長が隙間に対して短い場合
次の図を見てください。
この図は、波長が隙間に対して短かい場合です。
隙間から出た波を考えます。
やはり隙間には無数の点波源があります。
隙間が小さい時、図において 2 つの波源からの距離の差は非常に小さいと考えて良いでしょう。
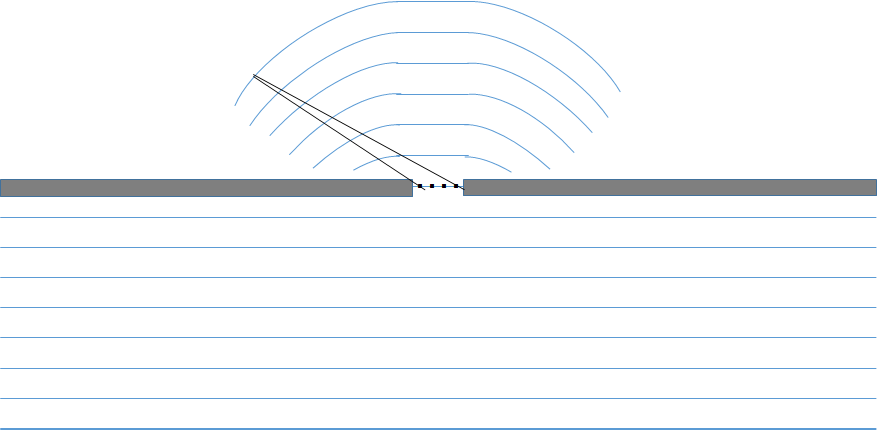
すなわち隙間から出る波の位相差はどれも少なく、波は減衰しません。
そのため、障害物の裏側まで回折した波が観察されることになります。
したがって、隙間に対して波長が短くなれば回折しにくくなり、ながければ回折しやすくなります。
これはレーザーによる回折格子の実験において非常に明るい点以外は、レーザー光の位相が揃わないため明るくならないことに似ています。




































コメント