概観
一般的な問題集で演習をしてきた人にとって,なじみの薄い問題設定でした。内容的には決して難しくはないのですが,慣れないぶん戸惑いを覚えた人も多かったと思います。私が解いた感想としては易化です。
しかし、こういった問題では,できるできないがはっきり分かれそう。
問題のパターンを覚えて解く,という勉強方法の人たちは苦戦したかもしれません。
2024年 共通テスト 物理 解説
問題はこちらから

第1問
問1
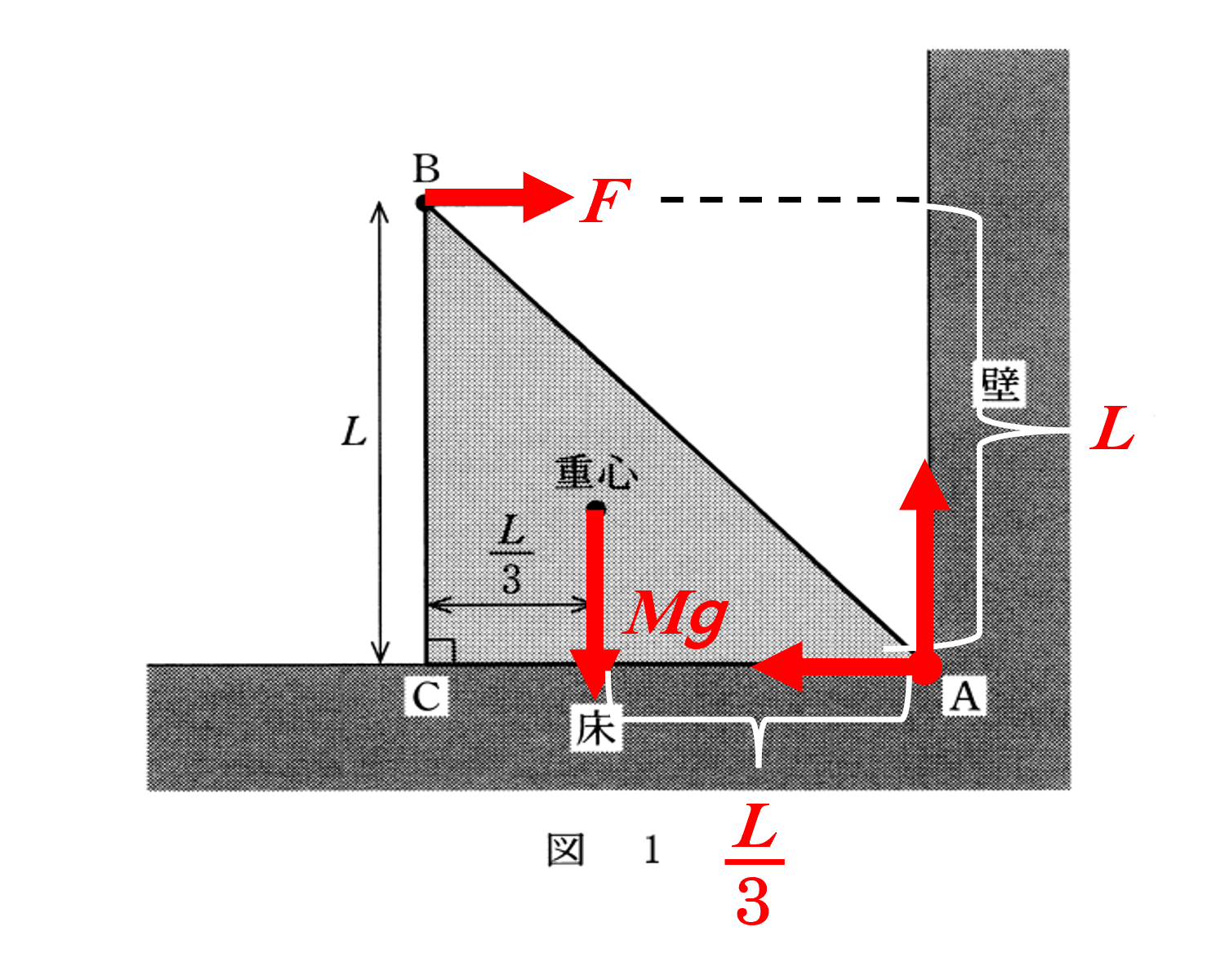
図のように力 $F$ を加えるとき,板がAのまわりに回転しないための $F$ の最大値を求めます。
これは,図と問題文がやや分りにくかったかもしれませんが,要は三角定規のBに力を入れて壁に押し当てている…という感じです。
Aまわりのモーメントを考えるため,図のようにします。
ここで
$F\times L=Mg \times \dfrac{2L}{3}$
ですから,$F=\dfrac{2Mg}{3}$
答え:⑤ 難易度:易
問2
この問題はボルツマン定数を使った式について正確に理解しているかを問うているのでしょう。
運動エネルギーは,ボルツマン定数 $k$ と絶対温度 $T$ を用いて, $\dfrac{3}{2}kT$ で示されることを知っていれば簡単です。太陽の中心部にあるヘリウム原子1個の運動エネルギーを $K$ ,温度 $300$ K の空気中にあるヘリウム原子1個の 運動エネルギーを $K_0$ とすると,辺々割って,
$\dfrac{K}{K_0}=\dfrac{\dfrac{3}{2}k\times 1500 \times 10^4}{\dfrac{3}{2}k\times 300}=50000$
答え 問題番号2:⑤ 難易度:易
また,運動エネルギーは絶対温度だけで決まりますから,水素原子とヘリウム原子それぞれ1個当たりの運動エネルギーの平均値は同じになります。
したがって,1倍
答え 問題番号3:③ 難易度:易
問3
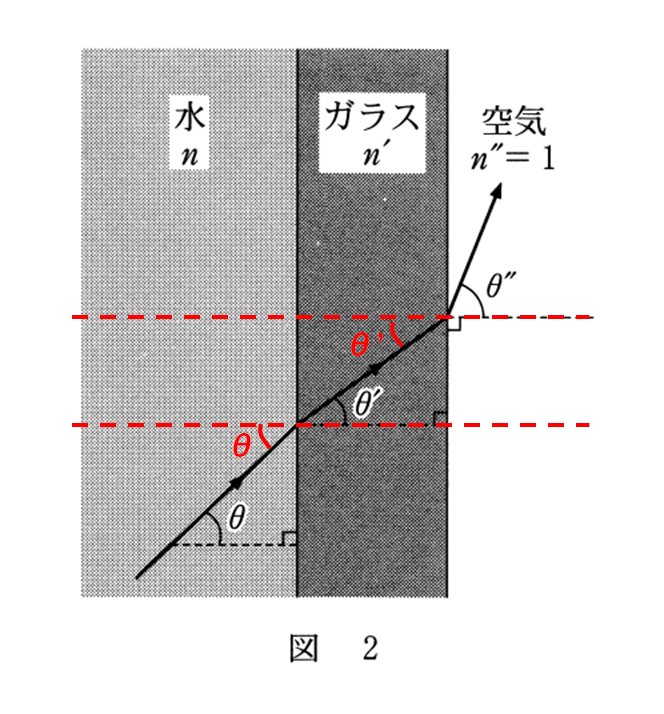
図のような場合,次の式が成り立ちます。
$n\sin{\theta}=n^{\prime}\sin{\theta^{\prime}}=n^{\prime \prime}\sin{\theta^{\prime \prime}}$
これは,屈折の法則から簡単に導けるのですが,一種の保存則のようですね。

$n_{12}=\dfrac{n_2}{n_1}=\dfrac{\sin \theta_1 }{\sin \theta_2}$ より,$n_1 \times \sin\theta_1=n_2 \times \sin\theta_2$
全反射する場合は,「屈折率大→屈折率小」となるようなときです。
つまり,次の図のような状態になっていると考えられます。すなわち,「ガラス→空気」 の場合です。
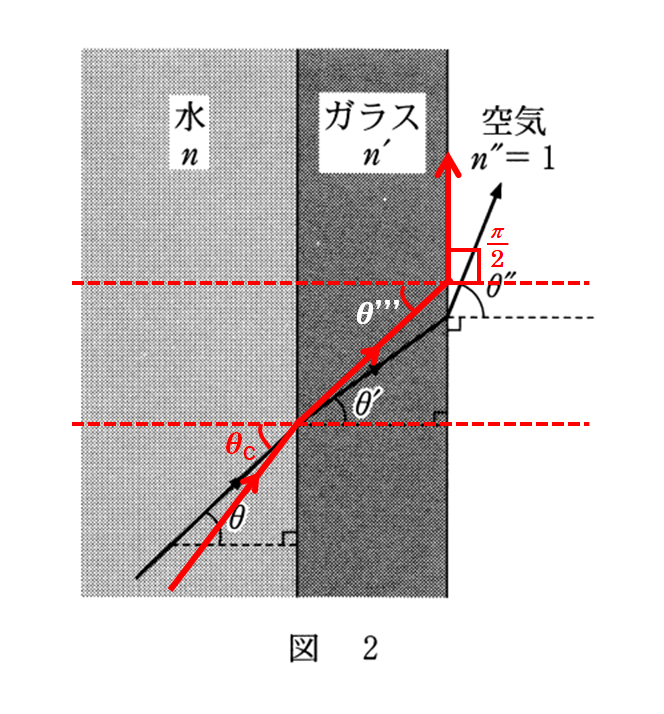
また,先ほどの保存則のような式を書くと,最後の屈折角が $90° =\dfrac{\pi}{2}$ であることに注意して,
$n\sin{\theta_c}=( n^{\prime}\sin{\theta^{\prime\prime\prime}})=1\times \sin{\dfrac{\pi}{2}}=1$
ゆえに,
$\sin{\theta_c}=\dfrac{1}{n}$
答え 問題番号4:④ 難易度:易
問4
ローレンツ力の基本的な事項が理解できていればOKです。
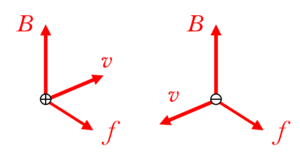
ローレンツ力 $f$ は,電荷 $q$ ,磁束密度 $B$ ,荷電粒子の速さ $v$ を使って,$f=qvB$ と示されます。荷電粒子の正負によらず,磁束密度 $B$ の向きは $f$ と $v$ に垂直になります。
この問題では,$xy$ 平面内で円運動しているため,向心力が必要です。向心力は $xy$ 平面内にあると考えられるため,磁束密度 $B$ は $xy$ 平面に垂直になり,$z$ 軸に平行となります。 ウ:$Z$ 軸
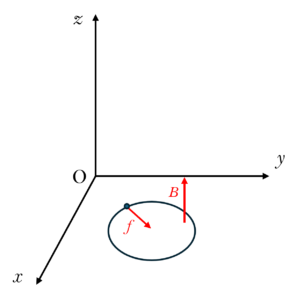
荷電粒子が $x$ 軸に平行に運動しているときは,荷電粒子は磁場から力を受けません。したがって,磁場の方向は $x$ 軸に平行になります。 エ:$x$ 軸
答え 問題番号5:⑦ 難易度:易
問5
反応式は次のようになります。
$\ce{^{1}_{1}H}+\ce{^{12}_{6}C}=\ce{^{13}_{7}N}$
反応前の全質量 ⇒ $1.0073+11.9967=13.0040$ u
反応後の全質量 ⇒ $13.0019$ u
したがって,
反応後の質量-反応前の質量=13.0019-13.0040=-0.0021 u
質量が減少していることから,その分のエネルギーが放出されています。 オ:放出された
半減期については,文字通り半分になるまでの時間です。
$N=N_0\left( \dfrac{1}{2} \right)^{\dfrac{t}{T}}$ より,
$\left( \dfrac{1}{2} \right)^{\dfrac{t}{T}}=\dfrac{1}{16}=\left( \dfrac{1}{2} \right)^{4}$
$t=40$ 分 したがって,
$\dfrac{40}{T}=4$
より,$T=10$ 分 カ:$10$分
答え 問題番号6:⑦ 難易度:易
第1問は全体的に基本的な内容です。ケアレスミスの無いように慎重に!
第2問
問1
ペットボトルが固定されている状態であることに注意します。
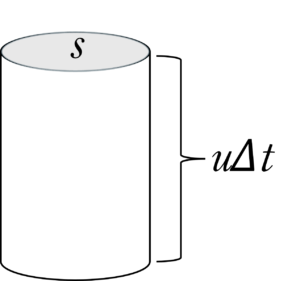
時間が短いという設定なので,噴出する水はノズル内の水とします。ノズルの断面積は $s$ で,速さ $u$ で水が噴出するため,$\Delta t$ の時間には,円筒形のノズルの体積 $\Delta V$ は,
$\Delta V= s \times u\times \Delta t $ ……①
となります(次図参照)。
また,$\Delta V$ はペットボトル円筒内でも同じ値のはずだから同様に考えて,
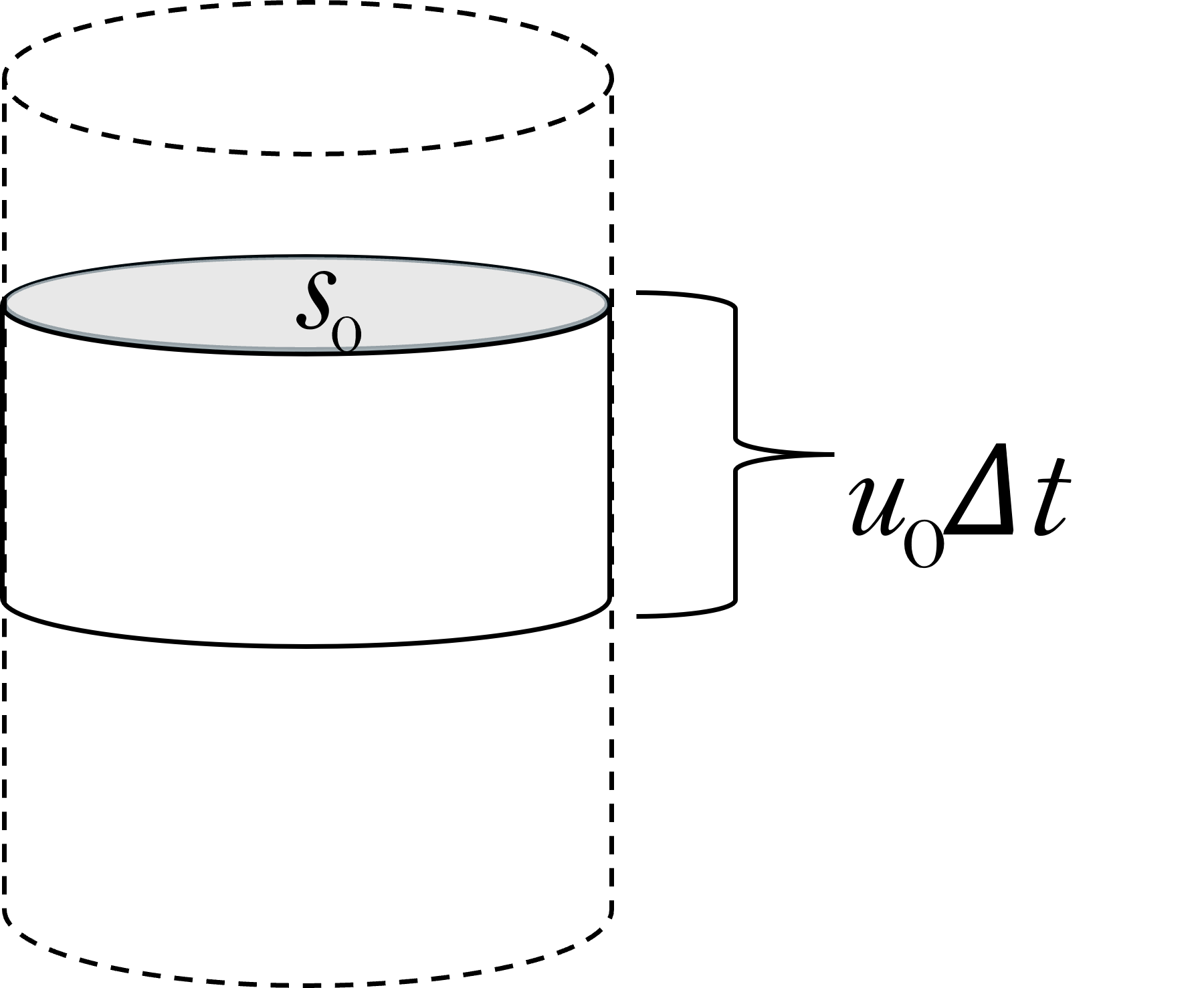
$\Delta V=s_0 \times u_0 \times \Delta t$ ……②
となります。
したがって,①②より,
$su\Delta t=s_0u_0 \Delta t$
より,
$u_0=\dfrac{s}{s_0}u$
答え 問題番号7:⑥ 難易度:易
問2
密度 $\rho=\dfrac{m}{V}$ より,
$\Delta m=\rho_0 \Delta V$
答え 問題番号8:② 難易度:易
$\Delta t$ 時間の間は,圧力一定とみなすので,圧縮空気がした仕事 $W$ は,$W^{\prime}=p\Delta V$ で示されます。
答え 問題番号9:① 難易度:易
問3
ウ:エネルギーの原理から
$初めの運動エネルギー+仕事=後の運動エネルギー$
ですから, ウ:(c) 運動エネルギー
$初めの運動エネルギー+仕事=後の運動エネルギー$
$0+W^{\prime}=\dfrac{1}{2}\Delta mu^2$
より,
$W^{\prime}=\dfrac{1}{2}\Delta mu^2$
$u=\sqrt{\dfrac{2W^{\prime}}{\Delta m}}$
よって, エ:(f)
答え 問題番号10:⑨ 難易度:易
問4
問題文中に近似の指示があるので注意します。
運動量保存則を適用します。最初の運動量は $0$ で,鉛直上向きを正とすると,
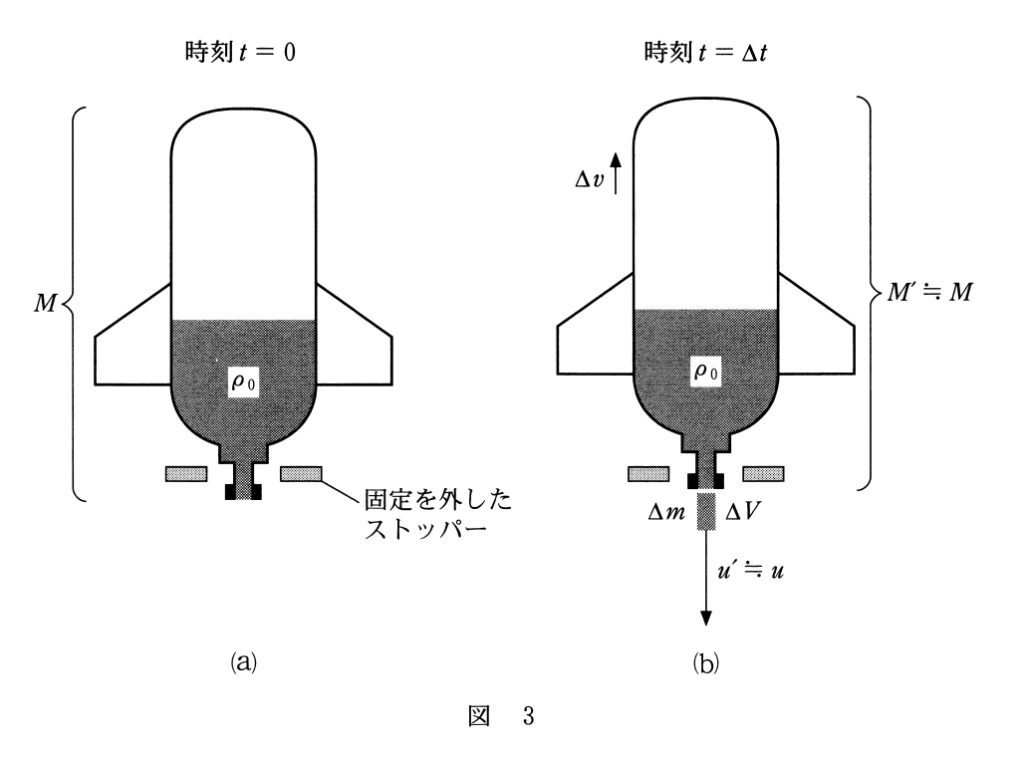
$0=M\Delta u-\Delta m u$
答え 問題番号11:④ 難易度:易
問5
運動量と力積の関係は次の式で示されます。
$最初の運動量+力積=後の運動量$
ペットボトル本体に対して考えることにします。
ペットボトルの最初の運動量は $0$ で,推進力 $F$ が $\Delta t$ の間持続し,質量 $M$ のペットボトルが鉛直上向きに $M\Delta v$ の運動量を得ると考えると,
$0+F\Delta t =M\Delta v$
より,
$F=\dfrac{M\Delta v}{\Delta t}$
これが重力 $Mg$ よりも大きくなるという条件から,
$F=\dfrac{M\Delta v}{\Delta t}>Mg$
よって,
$\Delta v>g\Delta t$
答え 問題番号12:④ 難易度:易
第2問は難しくはないのですが,問題文をきちんと読み取り思考する力が求められるでしょう。 戸惑った人も多いと思います。
第3問
問1
フレミングの左手則を思い出してください。
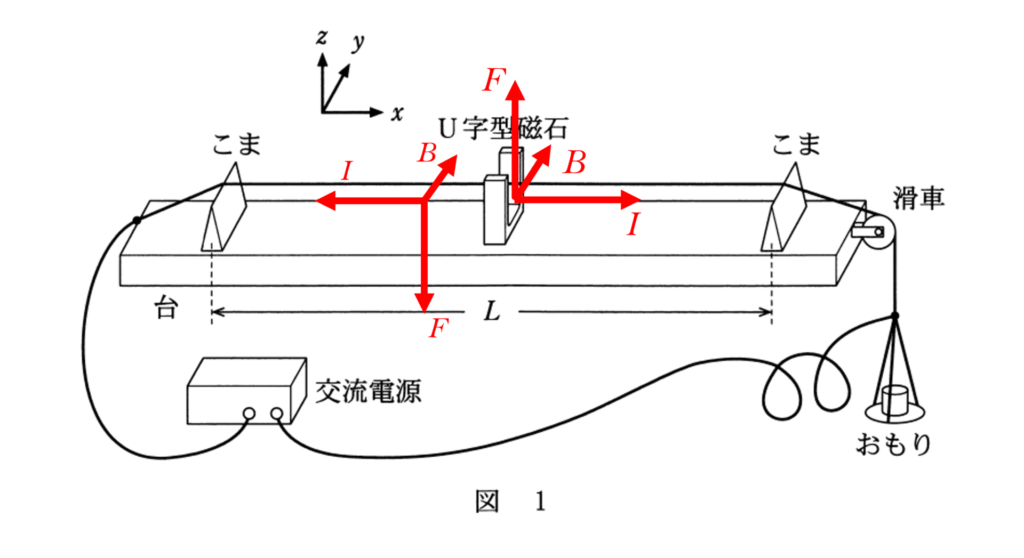
この場合,電流が導線をどちら向きに流れていても,また,磁石のNS極が反対でも,$z$ 軸に平行な力を受けることがわかります。ア:$z$ 軸
また,U字磁石の位置で大きく振動するはずなので,弦の中央部は「腹」となるはずです。イ:腹
答え 問題番号13:⑤ 難易度:易
問2
弦の中央が腹,全体で3個の腹を持ち,両端は節になります。
よって,次図のようになります。したがって,$\lambda=\dfrac{2L}{3}$
答え 問題番号14:③ 難易度:易

問3
次図より,腹の数が $n$ 個のとき,波長 $\lambda$ は,
$\lambda=2 \times \dfrac{L}{n}$
で示される。
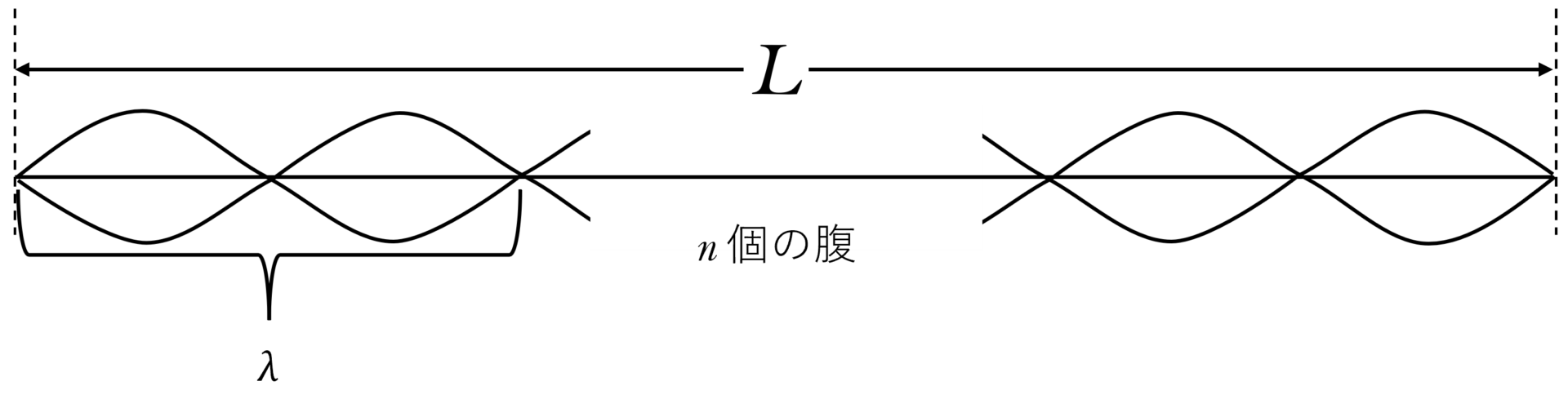
波の式 $v=f\lambda$ より,
$f=\dfrac{v}{\lambda}=\dfrac{v}{2 \times \dfrac{L}{n}}=\dfrac{v}{2L}\times n$
となるから,傾きは,$\dfrac{v}{2L}$ となり,弦を伝わる速さ $v$ に比例することがわかります。
答え 問題番号15:② 難易度:普通
問4
図より,$\sqrt{S}$ に比例することが読み取れます。
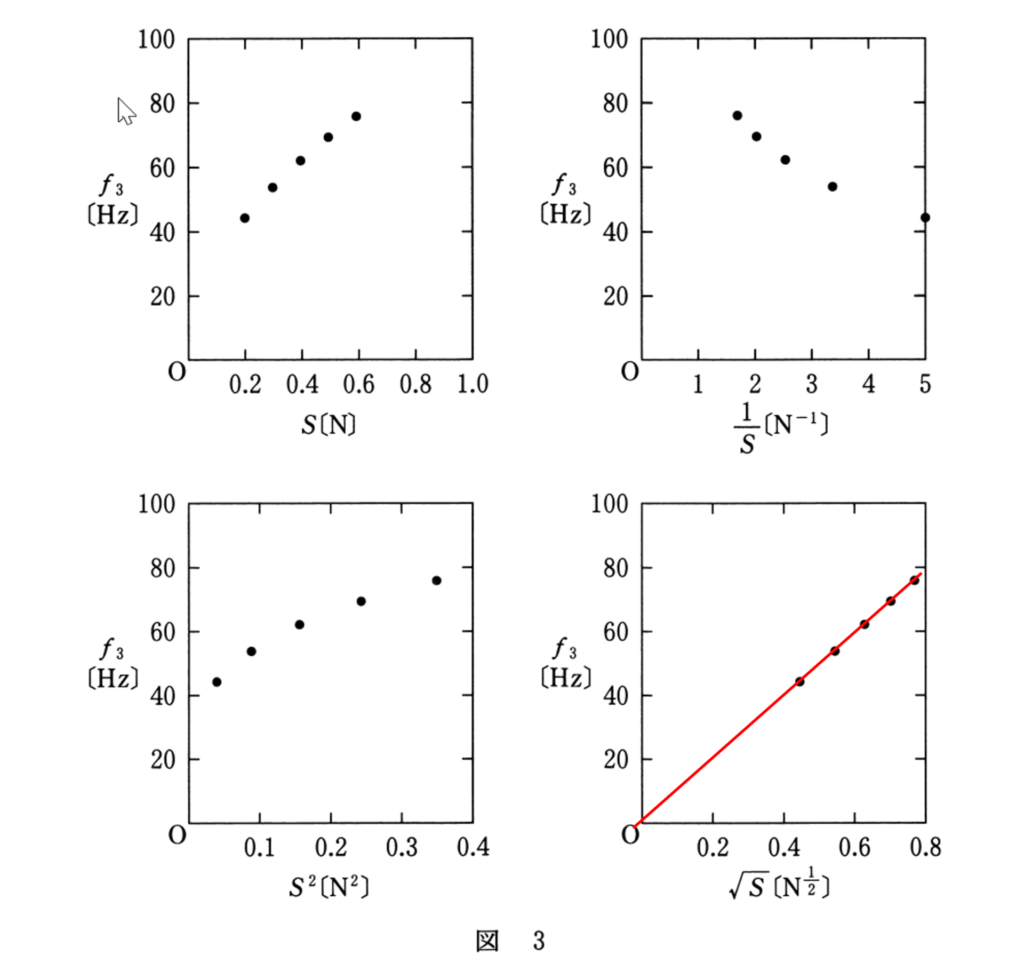
弦を伝わる波の速さ $v$ ,減の張力 $S$ ,線密度 $\rho$ として,
$v=\sqrt{\dfrac{S}{\rho}}$
であることを知っていれば,
$f=\dfrac{v}{\lambda}=\dfrac{n}{2L}\sqrt{\dfrac{S}{\rho}}$
から,ただちに $\sqrt{S}$ に比例することがわかります。
答え 問題番号16:② 難易度:普通
問5
| $d=0.1$ mm |
$d=0.2$ $~~=2\times 0.1$ mm |
$d=0.3$ $~~=3\times 0.1$ mm |
|
| $f_1$ | $29.4$ | $14.9\fallingdotseq \dfrac{29.4}{2}$ | $9.5\fallingdotseq \dfrac{29.4}{3}$ |
| $f_2$ | $89.8$ | $44.3\fallingdotseq \dfrac{89.9}{2}$ | $28.8\fallingdotseq \dfrac{89.9}{3}$ |
| $f_3$ | $146.5$ | $73.9\fallingdotseq \dfrac{146.5}{2}$ | $47.4\fallingdotseq \dfrac{146.5}{3}$ |
表を横に見ていくと,$d$ が2倍3倍となると $f_1$ ,$f_2$ ,$f_3$ ともに約 $\dfrac{1}{2}$ ,$\dfrac{1}{3}$ 倍となっているのが読み取れます。
表1をグラフ化すると,次のようになり,$\dfrac{1}{d}$ に比例($d$ に反比例する)ことがわかります。
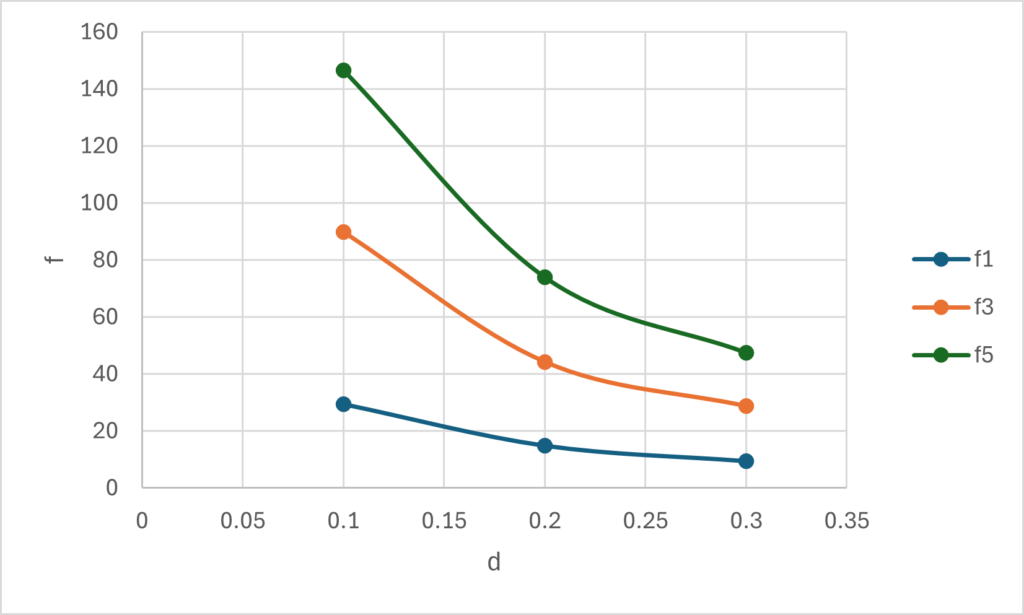
ちなみに,横軸を $\dfrac{1}{d}$ にとってグラフ化すると,
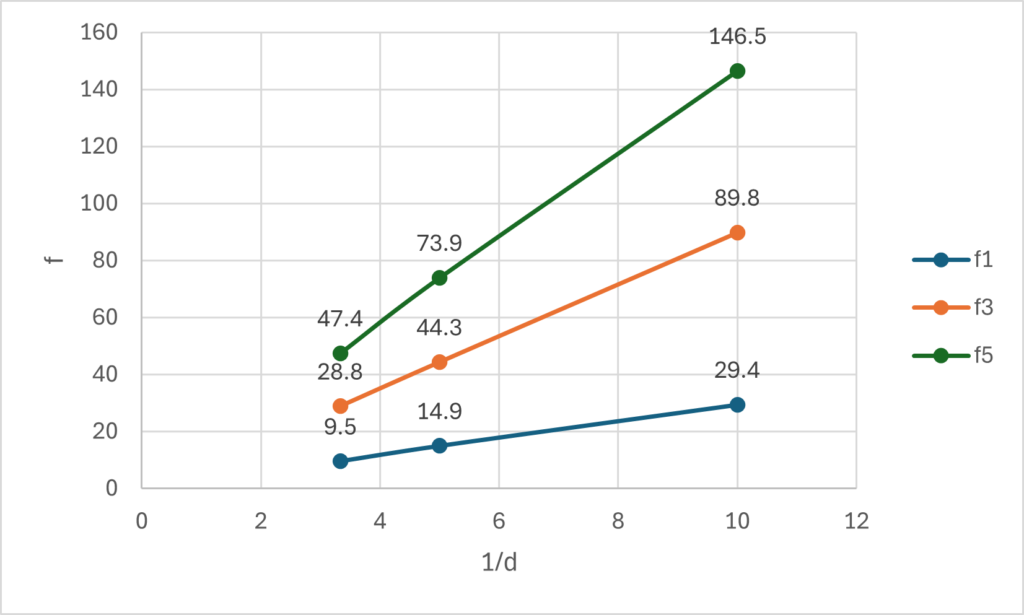
となり,$\dfrac{1}{d}$ に比例していることが明瞭になります。
答え 問題番号17:④ 難易度:普通
前問から,
$f=\dfrac{v}{\lambda}=\dfrac{n}{2L}\sqrt{\dfrac{S}{\rho}}$
この $\rho$ は線密度で $\dfrac{m}{L}$ で示される量です。これにより変形すると
$f=\dfrac{n}{2L}\sqrt{\dfrac{S}{\dfrac{m}{L}}}$
ここで,導線の密度(≠線密度)を $\rho_0$ としてやると,導線の体積 $V$ として,
$m=\rho_0\times V=\rho_0 \times \left( \pi d^2\times L \right)$
となりますから,
$f=\dfrac{n}{2L}\sqrt{\dfrac{S}{\dfrac{\rho_0\times \pi d^2\times L}{L}}}$
$f=\left ( \dfrac{n}{2L}\sqrt{\dfrac{S}{\rho_0 \pi}} \right) \times \dfrac{1}{d}$
より,比例定数 $k$ として,
$f=k\times \dfrac{1}{d}$
と書くことができます。
第4問
問1
点電荷があるとき,それを縦に割ってみた図です。
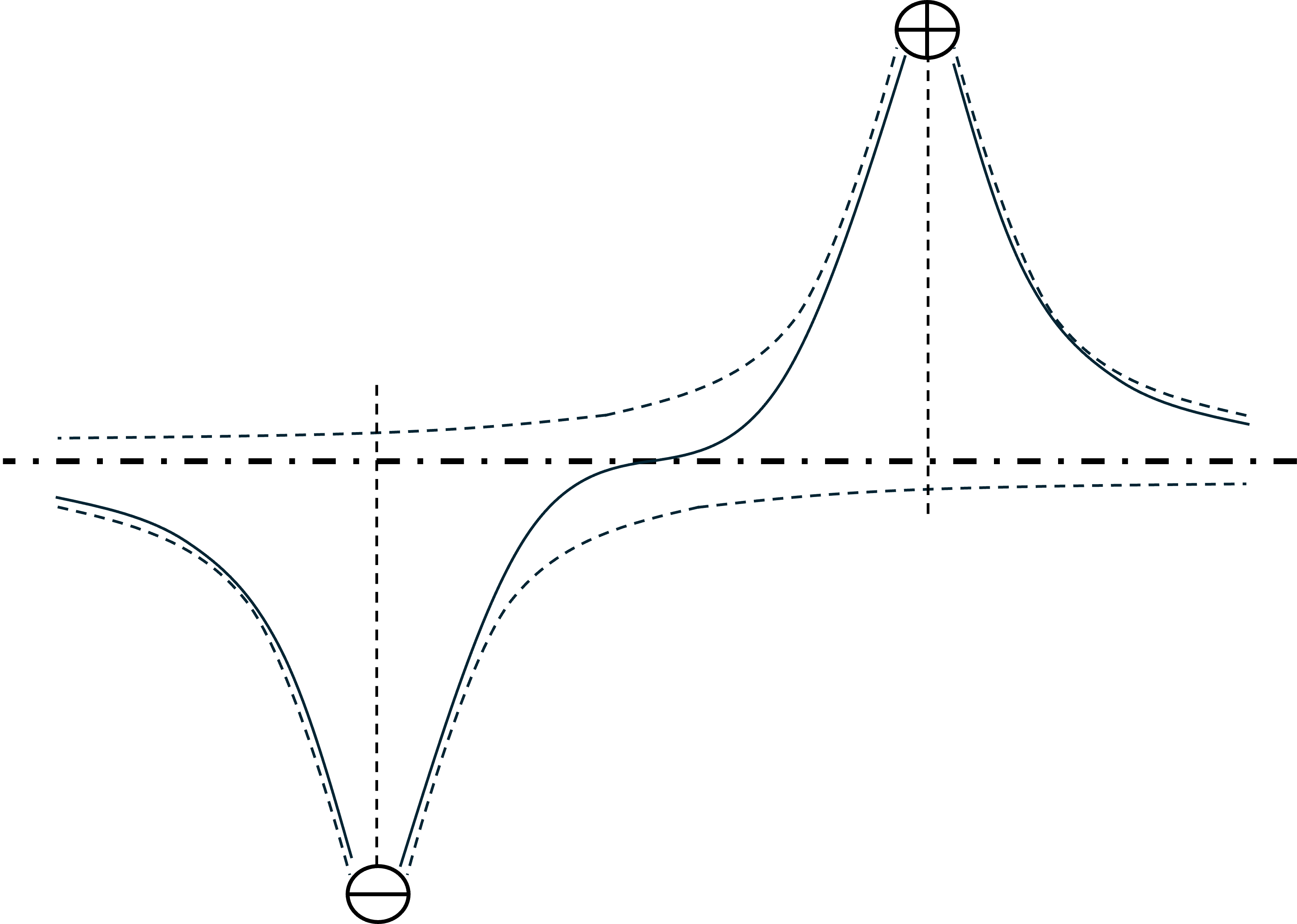
電位はこれらの山の等高線だと思えばよいです。
なぜならば,電位とは無限遠からその位置(高さ)まで試験電荷を運ぶ時の仕事で示されるからです。
上の図を例えば,富士山と駿河湾の深い海のようにイメージして等高線を考えてみると,
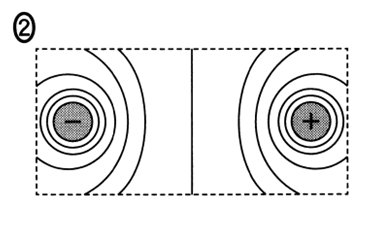
のようになります。
答え 問題番号18:② 難易度:易
問2
等電位線と電気力線についての基本的な知識を問います。
(a) 電気力線は,電場が強いところほど密である。〇
(b) すべての隣り合う等電位線の間の距離は等しい × ⇒ 電位は問1にあるように 無限遠からその位置(高さ)まで試験電荷を運ぶ時の仕事で示されます。必ずしも等間隔ということはありません。
(c) 等電位線と電気力線は直交する。〇
答え 問題番号19:⑤ 難易度:易
問3
電場,電気力線,電位,電流などに関する基本的な知識を問います。
前問にあるように電気力線と等電位線は直交するから,問題の図2に電気力線を書き入れてみると次図のようになります。
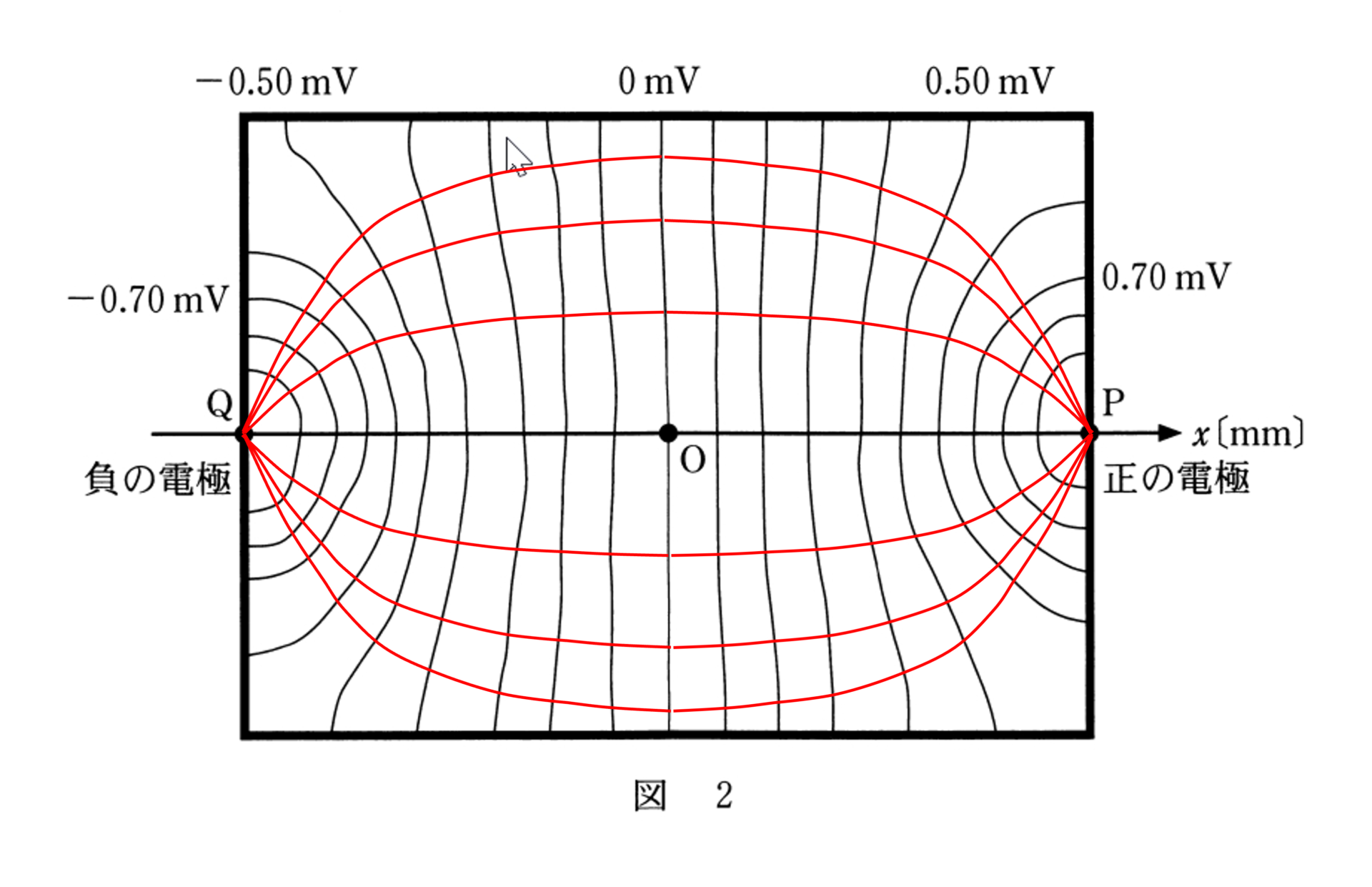
図から,導体紙の辺の近くの電場はその辺に「平行」であることがわかります(導体紙の横の辺を見るとわかりやすい)。
また,電流と電場の向きは「同じ」なので,辺の近くの電流はその辺に「平行」に流れていることがわかります。
答え 問題番号20:① 難易度:易

電流は電位の高いところから低いところへ流れます。
また,電場は電位の高いほうから低いほうへ向いています。
問4
一様な電場では次の式が成り立ちます。
$E=\dfrac{V}{d}$
すなわち,図3のグラフの傾きは電場を示しています。
グラフの $x=0$ ㎜ の位置付近では傾きが一定であるとみなせるため,図のように横軸と縦軸をとると,
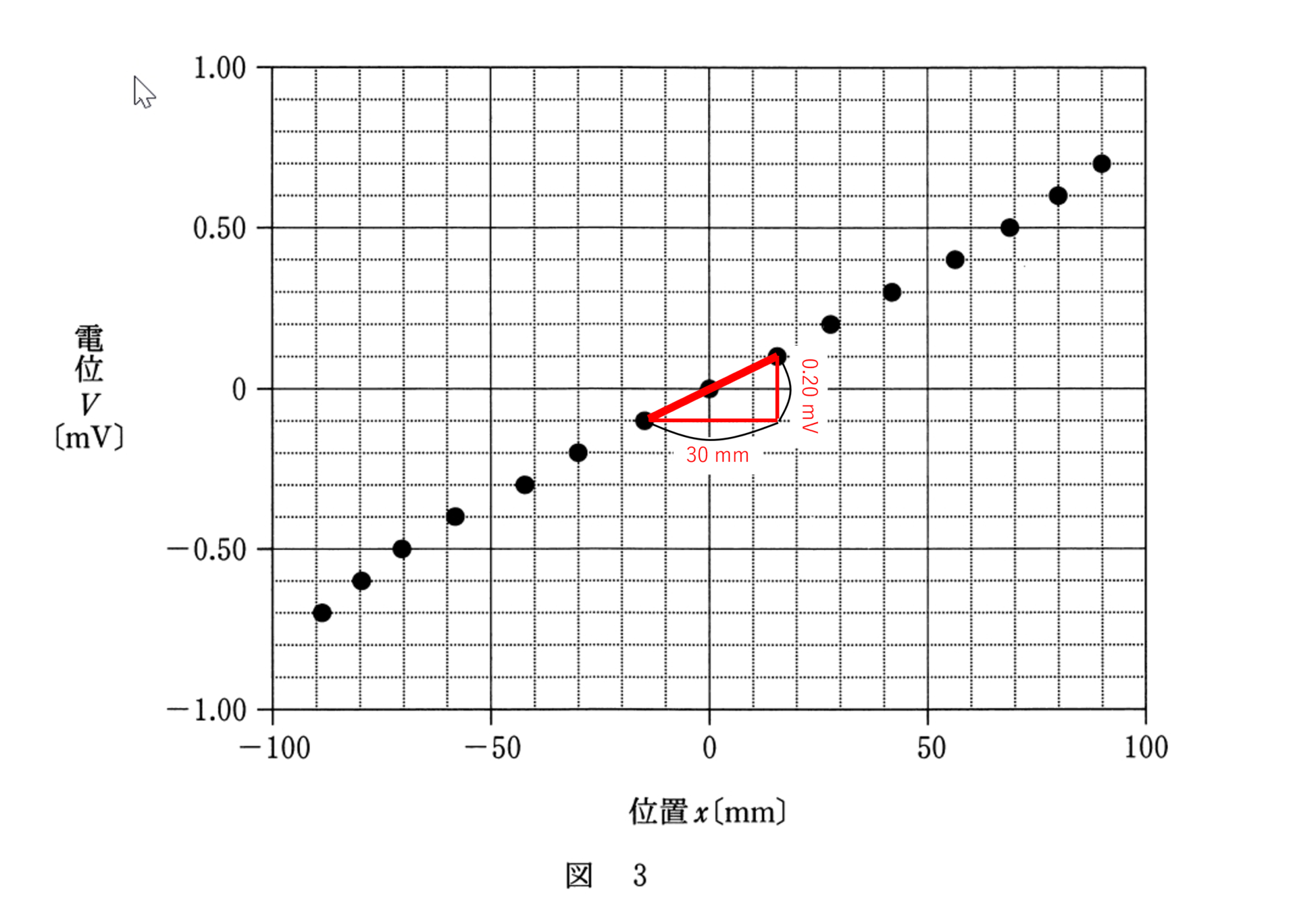
$E=\dfrac{0.20 \; \mathrm{mV}}{30 \; \mathrm{mm}}\fallingdotseq 7\times 10^{-3}$ V/m
答え 問題番号21:⑥ 難易度:易
問5
抵抗率 $\rho$ ,抵抗 $R$ ,導体長さ $l$ ,導体断面積 $S$ とすると,$R=\rho \dfrac{l}{S}$ で示されます。
ここで,$x=0$ を中心とする小さい幅を $\Delta d$ とし,その間の電位差を $\Delta V$ とすると,この近辺では電場の大きさ $E$ は一様とみなせるため,次の式が成り立ちます。
$E=\dfrac{\Delta V}{\Delta d}$
また,短い区間の抵抗を $R$ ,電流の大きさを $I$ とすると,$\Delta V= RI$ だから,
$E=\dfrac{\Delta V}{\Delta d}=\dfrac{RI}{\Delta d}$
$R=\rho \dfrac{l}{S}$ より,$R=\rho \dfrac{\Delta d}{S}$ を代入すると,
$E=\dfrac{\rho \dfrac{\Delta d}{S}I}{\Delta d}=\rho\dfrac{I}{S}$
したがって,
$\rho=\dfrac{SE}{I}$
答え 問題番号22:① 難易度:普通
ここで,$R=\rho \dfrac{l}{S}$ より,$\rho=\dfrac{RS}{l}$ となりますが,抵抗率 $\rho$ の単位は,$[\Omega \cdot m]$ であることがわかります。
$[\Omega \cdot m]=\left[ \dfrac{\mathrm{V}}{\mathrm{A}}\cdot m \right] $
答えがわかればよいのであれば,選択肢から該当する単位となるものを選ぶという考え方もできます。いざという時のために,次元解析も覚えておきましょう。







































コメント