光路長・光学的距離
光学的距離は、屈折率 $n$ 中の長さ $l$ が、真空中では $nl$ に相当するというように考えます。
物理のエッセンスの波動の55番についても解説していますので参考にしてください。
光路長・光学的距離
光路長・光学的距離は次のように定義されます。
光路長・光学的距離
屈折率 $n$ の媒質中の距離 $l$ は、真空中の距離 $n \times l$ (屈折率×距離)に相当する。
図のように、屈折率 $n$ の物質の中を光が進むことを考えます。
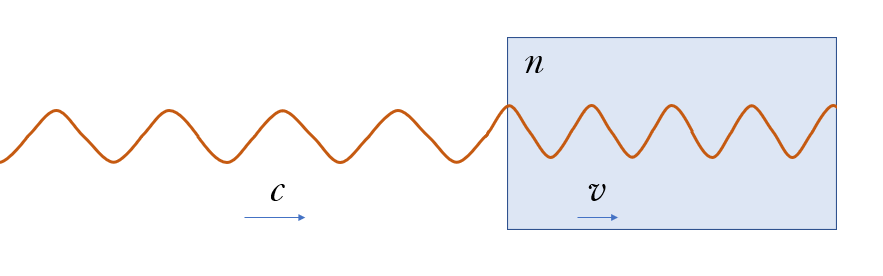
このとき、真空での波長 $\lambda$ 、物質内での波長を $\lambda^{\prime}$ とすると、屈折の法則より、
$n=\dfrac{\lambda}{\lambda^{\prime}}$
が成立します。これを変形すると、
$\lambda=n\times \lambda^{\prime}$
となり、真空中の波長 $\lambda$ は物質中の波長 $\lambda^{\prime}$ の $n$ 倍になります。
したがって、物質中の長さ $l$ 中と同じ数の波を含む長さは、真空中では $n$ 倍の $n\times l$ になるはずです。
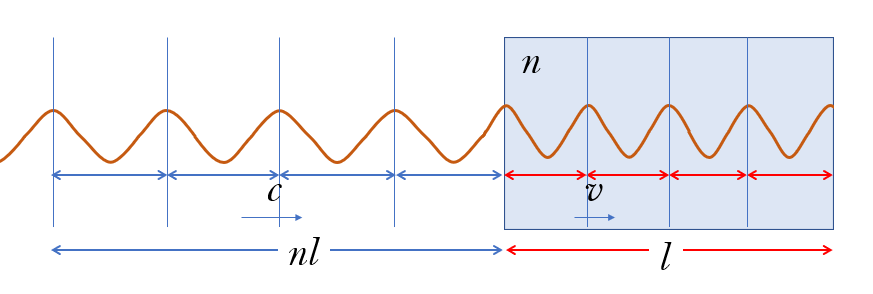
よって、屈折率 $n$ の媒質中の距離 $l$ は、真空中の距離 $n \times l$ (屈折率×距離)に相当する・・ということになります。
あるいは、
真空中での光速を $c$ とし 、物質中では光速 $v$ で進むとすると、屈折の法則から次の関係式が導かれます。
$n=\dfrac{c}{v}$
より、$c=n\times v$ $(n>1)$
つまり、真空中の光速は物質中の $n$ 倍です。
ということは、一定時間、真空中で光が進む距離は物質中の $n$ 倍です。
したがって、物質中の距離 $l$ は、真空中では $n$ 倍の $n\times l$ に相当するというわけです。
式でやってみましょう
時間 $t$ で進む距離を考えます。真空中で進む距離を $l_0$ として、
真空中:$l_0=ct$
物質中:$l = vt$
辺々割ると、
$\dfrac{l_0}{l}=\dfrac{ct}{vt}=\dfrac{c}{v}$
屈折率から $c=nv$ なので
$\dfrac{l_0}{l}=\dfrac{c}{v}=\dfrac{nv}{v}=n$
したがって、
$l_0=nl$
動画
光路長・光学的距離の何が便利なのでしょうか?
物理のエッセンスの問題を参照してください。
波動 55番 P136





































コメント