加速度

加速度は、物理を勉強するときでも、最初のほうで出てくる事柄です。

加速度って、物理ではものすごく基本的なことなのですが、日常生活では厳密な意味で使うことは、あまりありません。

そのためか、意外とあやふやだったりします。

しかし、物理で加速度があやふやだということは、その後のほぼすべてのことについて、あやふやなままです。

加速度の「公式」など、数Ⅱで習う簡単な微積が理解できていれば、覚えることはほぼありません。

ただの「公式」暗記だけにとどまらず、その意味についてよく理解しておきましょう。

加速度

直線運動の加速度

一直線上を運動する物体の速度変化について考えましょう。

一直線上を運動しているある物体の速度が、時間 $\Delta t$ の間に、$v_0$ から $v$ に変化したとすると、

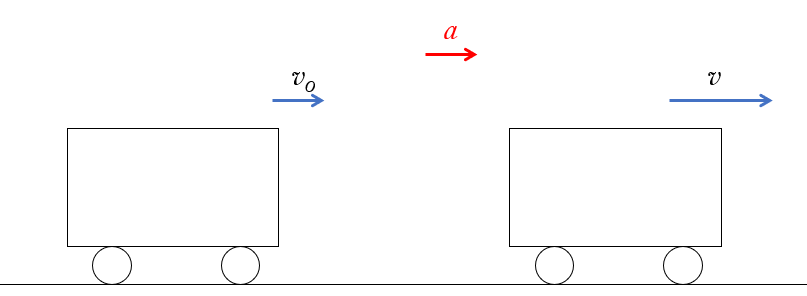
その間の単位時間当たりの、平均の速度の変化量を、平均の加速度といい $\bar{a}$ として示します。

$\bar{a}=\dfrac{v-v_0}{\Delta t}=\dfrac{\Delta v}{\Delta t}$

この $\Delta t$ を限りなく $0$ に近づけていく（ $t$ で微分する）と、瞬間の加速度を得ることができます。

そして、それは $v-t$ グラフの接線の傾きで示されます。$\because \:\: \bar{a}=\dfrac{\Delta v}{\Delta t}$

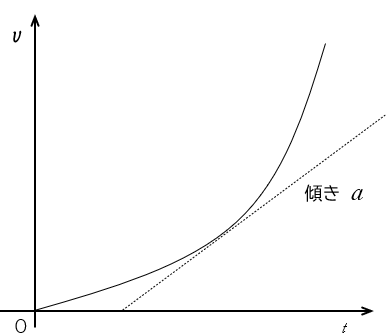
単位は $\mathrm{m/s^2}$ で「メートル毎秒毎秒」と読みます。

加速度の向き

直線運動の場合の加速度は、正負の記号でその向きを示すことができます。

例えば、

だんだんと速くなる運動

図で右方向を正の向きとします。

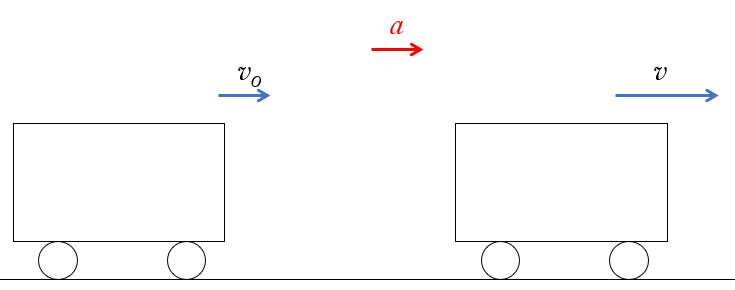
$v>v_0$　であるから、 $\bar{a}=\dfrac{v-v_0}{\Delta t}>0$　となり、加速度のベクトルは図の右方向へ向いています。

だんだんと遅くなる運動

図で右方向を正の向きとします。

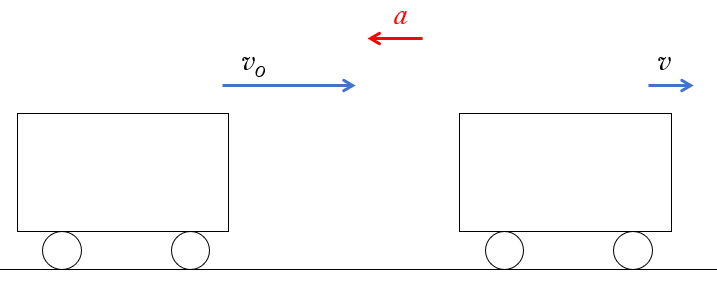
$v<v_0$　であるから、 $\bar{a}=\dfrac{v-v_0}{\Delta t}<0$　となり、加速度のベクトルは図の左方向へ向いています。

等加速度直線運動の例

例えば、図の右向きを正として

次の図のように1秒ごとに規則正しく $2\:\mathrm{m/s}$ づつ速くなる場合の加速度は、$2\:\mathrm{m/s^2}$

1秒ごとに規則正しく $2\:\mathrm{m/s}$ づつ遅くなる場合の加速度は、$-2\:\mathrm{m/s^2}$

と示すことができます。

加速度の大きさは、簡単に言うと、1秒あたりにどれだけずつ速くなるか？ということですね。（MKS単位系）

直線運動ではさらに、± で向きを表します。

平面運動の加速度

一般に、運動は一直線上だけではなく、平面、あるいは空間で運動をします。

そのため、加速度についても一般的に考えれば、ベクトル的に考えて次のように表現できます。

ある点から運動したとき、かかった時間が $\Delta t$ で、速度ベクトルが $\vec{v_0}$ から、$\vec{v}$ へと変化したとします。

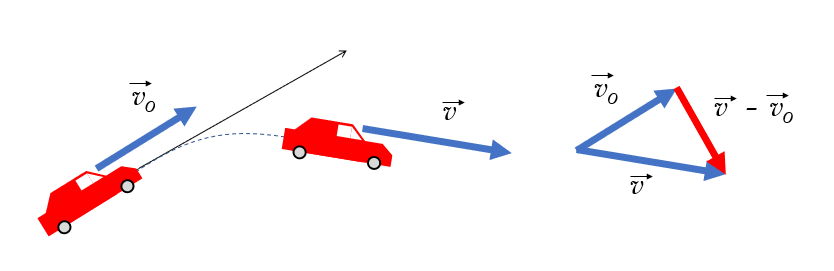
そのときの加速度ベクトル $\vec{v}$ は、

$\vec{a}=\dfrac{\vec{v}-\vec{v_0}}{\Delta t}=\dfrac{\Delta \vec{v}}{\Delta t}$

で示されます。

一直線上の場合と同様に、$\Delta t$ を限りなく $0$ に近づけると（ $t$ で微分すると）、瞬間の加速度を得ることができます。

等加速度直線運動

問題を考えるときは、2次元的・3次元的な運動であっても、変位・速度・加速度を $x-y-z$ 方向などに分解して考えることが多くなります。

そうすると、それぞれの方向では等加速度直線運動を考えればよいので、計算が簡単になります。

加速度が一定であるとすると、
一直線上の運動での加速度を $a$ 、時刻 $t$ での速度、変位をそれぞれ $v$、$x$ とし、時刻 $0$ のとき原点を初速度 $v_0$ で通過したとすれば、

$a=\dfrac{v-v_0}{t}$　より、

$v=v_0+at$

グラフに示すと次の図になります。

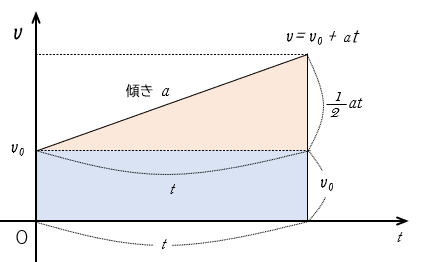
この時の変位 $x$ は $v-t$ グラフと $t$ 軸で囲まれる面積であることから、

$x=(v_0\times t)+\left(t\times at\div{2}\right)=v_0t+\dfrac{1}{2}at^2$

と示されます。

これらの2式から $t$ を消去するため、$v=v_0+at$　より、$t=\dfrac{v-v_0}{a}$　として、$x=v_0t+\dfrac{1}{2}at^2$　へ代入します。

すると、

$x=v_0t+\dfrac{1}{2}at^2=v_0(\dfrac{v-v_0}{a})+\dfrac{1}{2}a(\dfrac{v-v_0}{a})^2$

これより、

$v^2-v_0^2=2ax$

を得ます。

微積でやってみよう

積分してみます

まず、$a=\dfrac{dv}{dt}$　ですから、この両辺を $\int{dt}$　します。

$$\int{a}dt=\int{dv}$$

より、加速度が一定であるとすれば $C$ を積分定数として、

$$at+C=v$$

$t=0$　のとき、$C=v_0$　とすると、

$$v=v_0+at$$

となります。
これをさらに、 $\int{dt}$　します。

$$\int{v}dt=\int{(v_0+at)dt}$$

$x=\int{v}dt$　なので、やはり積分定数を $C$ とすると、

$$x=v_0t+\dfrac{1}{2}at^2+C$$

$t=0$　のとき、$x=0$　とすると、$0=0+0+C$　より、$C=0$　ですから、

$$x=v_0t+\dfrac{1}{2}at^2$$

微分してみます

$x=v_0t+\dfrac{1}{2}at^2$　の両辺を $t$ で微分してみましょう。

そうすると、

$$v=\dfrac{d}{dt}x=v_0+at$$

加速度の意味をしっかり理解できていれば、微積を使うことで、覚えることはほぼありません。

まとめ

等加速度直線運動

$v=v_0+at$

$x=v_0t+\dfrac{1}{2}at^2$

$v^2-v_0^2=2ax$