速度と速さ
日常生活では、これらの区別はあまりしていませんが、物理では速度と速さはちょっと違います。
詳しく言うと、
- 速度・・・ベクトル量
- 速さ・・・スカラー量
ベクトルとは、向きと大きさをあわせもつ量です。他には、力があげられます。
スカラーとは、大きさのみの量です。他には、温度があげられます。
速さ
速さは速度の向きをとって、大きさのみを示したものです。
簡単に言うと、自動車のスピードメーターを見ていると考えてもらえればいいでしょう。

自動車のスピードメーターは、いま時速何キロ出ているかはわかりますが、どこへ向かっているかは、メーターを見ているだけではわかりませんね。
今、時間 $t$ で $x$ だけ移動したとすると、速さ $v$ は、
$v=速さ=\dfrac{距離}{時間}=\dfrac{x}{t}$
で示されます。
これは日本語で説明するなら、速さとは「単位時間(1秒間)に移動する距離」の意味です。
ただし、実際に単位時間(1秒間)移動する必要はなく、今の速さのまま運動したら、1秒間でそれだけ移動する・・という意味です。
(注:時間はなにも1秒間とは限りません。1時間でも1日でもOKです。)
小学校や中学校の参考書などを見ていると、まれに「きはじ」とか「はじき」とかの説明を見ることがあります。
みなさんは、少なくともこのようなものを、ただ暗記することはやめましょう。
それよりも、速さとは「単位時間(1秒間)に移動する距離」の意味・・であることを理解してください。
それで十分です。
それでは、練習として $\mathrm{km/h}$ と $\mathrm{m/s}$ の換算をしてみましょう。
問題
- $72\:\mathrm{km/h}$ を $\mathrm{m/s}$ に直せ。
答え
$72\:\mathrm{km/h}=72\times \dfrac{1000 \mathrm{m}}{ 3600 \mathrm{s}}=20\:\mathrm{m/s}$
- $10\:\mathrm{m/s}$ を $\mathrm{km/h}$ に直せ。
答え
$10\:\mathrm{m/s}=10\times\dfrac{10^{-3}\:\mathrm{km}}{\frac{1}{3600}\:\mathrm{h}}=36\:\mathrm{km/h}$
ですが、一般化すると、
$A\:\mathrm{km/h}=A\times\dfrac{1000 \mathrm{m}}{ 3600 \mathrm{s}}=A\div{3.6}\:\mathrm{m/s}$
$B\:\mathrm{m/s}=B\times\dfrac{10^{-3}\:\mathrm{km}}{\frac{1}{3600}\:\mathrm{h}}=B\times{3.6}\:\mathrm{km/h}$
ですから、$\mathrm{km/h}$ を $\mathrm{m/s}$ に直すときは、$3.6$ で割り、$\mathrm{m/s}$ を $\mathrm{km/h}$ にするときは、$3.6$ をかけてやればよいことになります。
等速直線運動のグラフ
一直線上を等速で運動する物体の速さや距離と時間の関係をグラフにしてみましょう。
まず $x-t$ グラフです。
これは、 $v=\dfrac{x}{t}$ より、 $x=vt$ ですから、原点を通る直線になります。
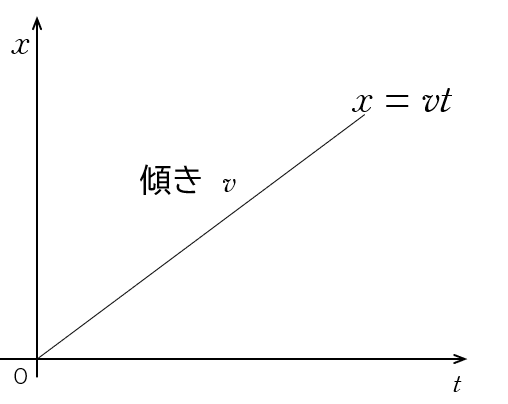
この直線の傾きが $v$ を示しています。なぜなら、$v=\dfrac{x}{t}$ だからです。
つぎに、$v-t$ グラフを考えてみましょう。
これは、等速なのですから $v=$一定 のはずですね。
したがって、$v-t$ グラフは $t$ 軸に平行なグラフになります。
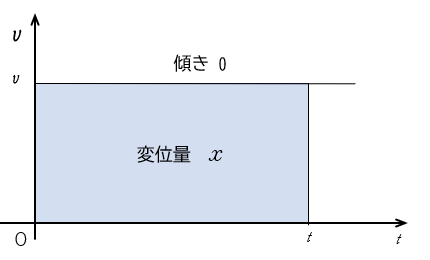
ことのき、ある時間 $t$ のときに、グラフと $t$ 軸のつくる四角形の面積が移動距離を示しています。
なぜなら、 $x=vt=$ 縦 × 横=四角形の面積 だからです。
速度
速度と速さの違いは、普段の生活ではあまり気にする人はいないかもしれません。
しかし物理では、速度と速さは明確に違います。
速度は先にあげたように、ベクトル量です。速さはスカラー量です。
つまり、速度とは速さ(大きさ)とどちらに向かっているか(向き)の両方をいっぺんに考えようというものです。
たとえて言うなら、カーナビの表示に向きと速さを表す矢印を付けたもの・・・というイメージです。
車が速く走っているときは、矢印の長さが長くなり、矢印は移動している方向に向いている・・と想像してください。
速度はこのように、矢印で表すと、その「速さ」「向き」を一度に示すことができて便利なのです。
このように、図に表記するときは矢印で示します。
矢印で示すことができるのがベクトルです。
また、記号表記するときは、ベクトルであることを明確にするために $\vec{v}$ のように、矢印を付けたり、 文字を太字にしたりします。
また、ベクトルを使う理由は・・便利だから・・です。
平面運動の速度
運動する物体の位置ベクトルを考えて平均の速度を求めてみます。

図では、時間 $\Delta t$ の間に、自動車の位置ベクトルが $\vec{r_P}$ から $\vec{r_Q}$ へと変化したとします。
そうすると変位ベクトル $\Delta \vec{r}$ が、$\Delta \vec{r}=\vec{r_Q}-\vec{r_P}$ であるので、この間の平均の速度 $\vec{\bar{v}}$ は次の式で示されます。
$\vec{\bar{v}}=\dfrac{\Delta \vec{r}}{\Delta t}=\dfrac{\vec{r_Q}-\vec{r_P}}{\Delta t}$
ここで、$\Delta t$ を $0$ に近づけてやれば、$P$ 点での、自動車の瞬間の速度になります。
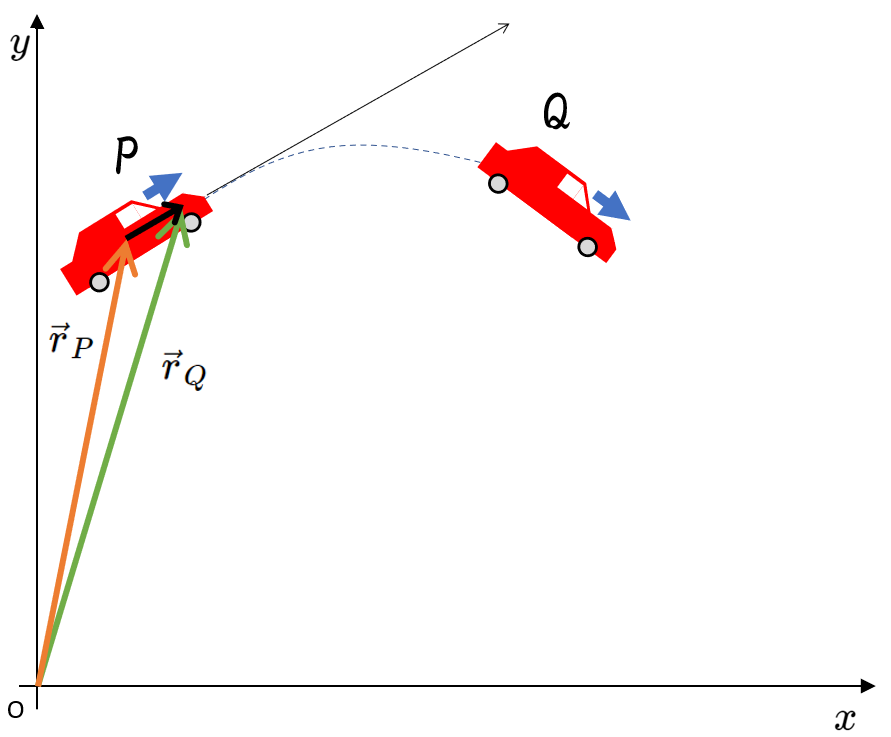
そしてそれは、$P$ 点における運動の経路の接線で示されます。
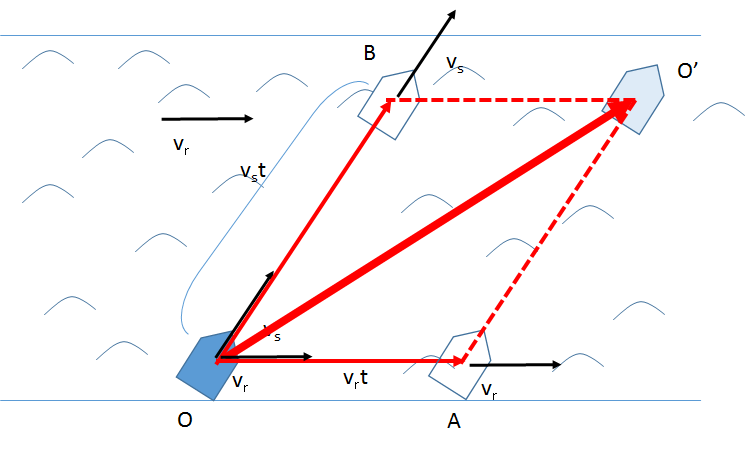
速度の合成・分解
さらに、速度はベクトルなので、分解合成を考えることができます。
相対速度
相対速度は非常に重要で有用な概念です。
以下で解説しています。
解説

物理のエッセンスの問題





































コメント