加速するエレベーター内でものを落としたり投げたりした場合にどのように解けば良いでしょうか?
ちょっと考えると難しい印象を受けます。
しかし、慣性力の考え方を使えば簡単にできてしまいます。
この記事で解説していきますね。
こちらの記事も参考に!

加速するエレベーター
エレベーターが加速運動しているとします。
等速運動の場合は内部は静止状態と同じ物理法則が働きますのでここでは省きます。
上へ加速する場合
エレベーターが鉛直上向きに加速度 $a$ で運動しています。
このとき慣性力はどちらへはたらくでしょうか?
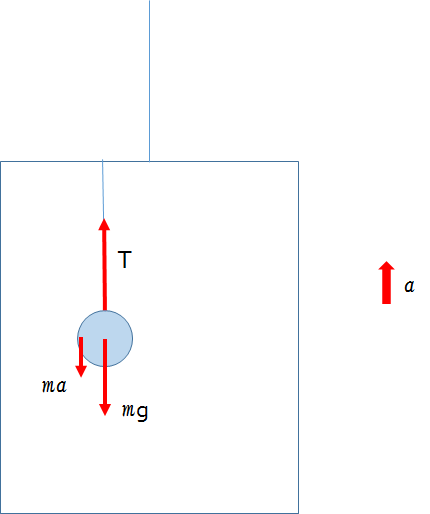
そうですね。慣性力は加速度とは逆向きに $ma$ ですから、この場合は下向きに慣性力がはたらきます。
エレベーター内に吊るされたおもりが静止している場合は、おもりに働く力がつりあっています。
したがって、次の式が成り立ちます。
$T=mg+ma$
よって、
$T=m(g+a)$
$T=mg’$
ただし、$g’=g+a$ とします。
このように変形すると、おもりに働く重力加速度が、$g$ から $g’$ へと変化したとも取れます。
つまり、加速するエレベーター内では重力加速度が $g’=g+a$ の世界だと考えればよいのです。

もし糸が切れれば、物体はエレベーター内では $g’=g+a$ の重力加速を受けて落下します。
したがって、余計なことは考えずに普通に落下公式を活用すればOKです。
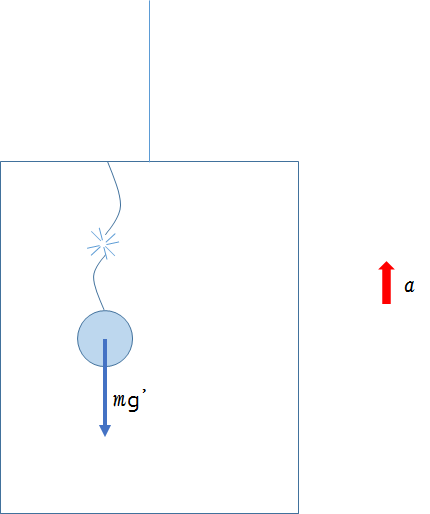
つまり、落下公式
$v=v_0+g’t$
$y=v_0t+\dfrac{1}{2}g’t^2$
$v^2-v_0^2=2g’y$
などです。他に斜方投射などした場合も、重力加速度を $g’=g+a$ とすればOKです。
下へ加速する場合
この場合も考え方は同様です。
すなわち、慣性力を考えます。
加速度とは逆向きに $ma$ ですから、この場合は上向きに慣性力がはたらきます。
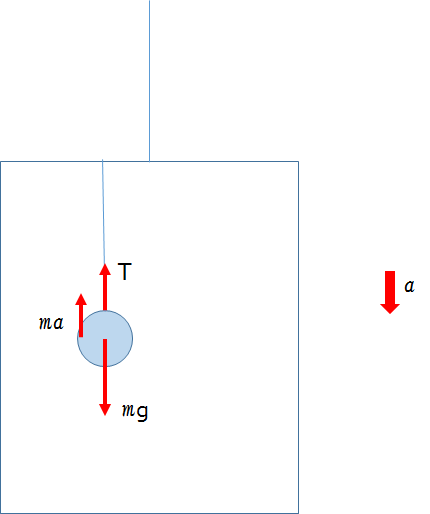
エレベーター内に吊るされたおもりが静止している場合は、おもりに働く力がつりあっています。
したがって、次の式が成り立ちます。
$T+ma=mg$
よって、
$T=m(g-a)$
$T=mg’$
ただし、$g’=g-a$ とします。
その他は同じですね。
新しい重力加速度に従って、静止しているエレベーター内での運動と考えればOKです。
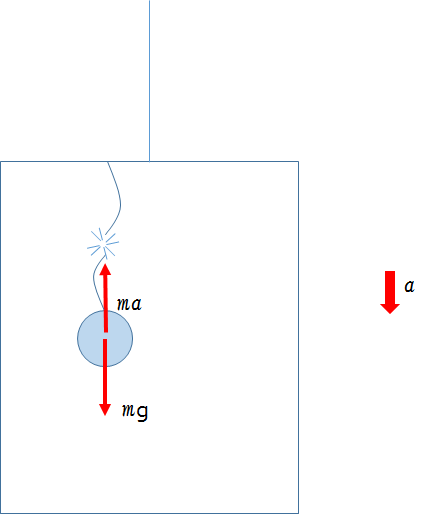
エレベーターが自由落下していれば?
自由落下ということは、$a=g$ ですね。
エレベーターが自由落下していれば、その場合は上記の「下へ加速する場合」での重力加速度の式
\begin{eqnarray}
g&’=&g-a\\
& =&g-g\\
&=&0
\end{eqnarray}
です。ということはエレベーター内は中に乗っている人から見れば重力のない世界・・・・無重量状態です。
宇宙空間でのエレベーター内
もしも、重力のない宇宙空間で加速度 $g$ でかっ飛んでいるエレベーターがあったとすると、その中では擬似的な重力加速度 $g$ がはたらき、地球上での万有引力と同じ擬似的な重力を感じます。
つまり、エレベーターの中は地球上にいるのと全く同じ感覚になるはずです。
しかし、片方は万有引力による重力、片方は慣性力による擬似重力です。
エレベーターの中に乗っている人は外が見えなければ、これらを区別することはできません。
これに意味を見出したのがアインシュタインというのは有名な話で、これにより一般相対性理論の着想を得たのです。
エレベーター内での運動
話を地球上に戻しましょう。
エレベーターの下向きの加速度が最大になるとき・・・・
(・・・上向きに運動していたエレベーターが止まる瞬間がいいでしょう)
に、エレベーター内でジャンプすれば・・・
・・・不思議!体が軽くなったように高く飛ぶことができます。
反対に、エレベーターの上向きの加速度が最大になる瞬間・・・・
・・・エレベーターが上向きに動き出す瞬間に同じようにジャンプしてみたら・・・
・・・今度は体が鉛のように重く感じられるはずです。
慣性力を本当は無い!とか書いてあるのを見ますが、このようなときには少なくともエレベーター内の人にとって見れば本当に感じる「実在の」力ですね。
注意:実際にやってはいけません。エレベーターが誤作動します。
ちょっと体を浮かせるとかぐらいにしておいてください。
慣性力のクイズです





































コメント