2点波源による波の干渉はポピュラーなものですね。
しかし、2点波源の一直線上の波源の外側はどうなっているのでしょうか?
定常波でしょうか?いえ!定常波にはなりません。
ここでは見落としがちなこのことについて考えてみましょう。

2点波源による干渉縞
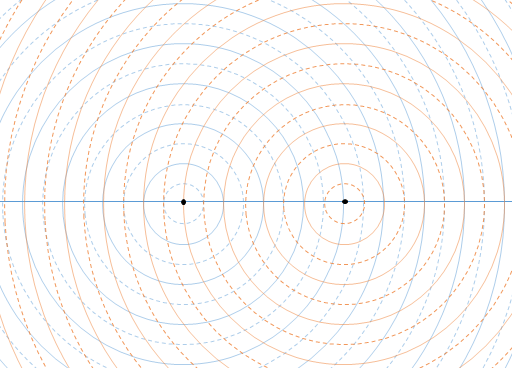
図のように平面上で2点波源がそれぞれ同位相で同じ波(同じ振動数・波長)を出している場合、
平面上では干渉縞が見られます。(図の実線は波の山を、点線は波の谷を示しています)
ここまではよくある話ですね。
問題はここからです。
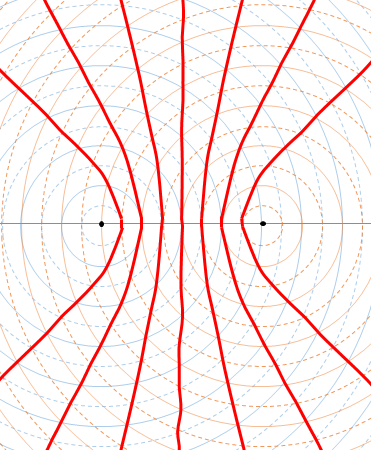
頭にあるような波源を結んだ一直線上の波の振動状態について考えます。
このとき、波源の間は定常波が作られますね。

しかし、波源の外側(青で囲った部分)はどうなんでしょうか?
定常波?
いえここは定常波になりません。
ここは進行波になるか打ち消し合うかです。
進行波とはどのようなものでしょうか?
ここで言う進行波とは定常波のようにその場で停止しているのではなく、動いていってしまう波のことです。
この図で波源の右外側を考えます。
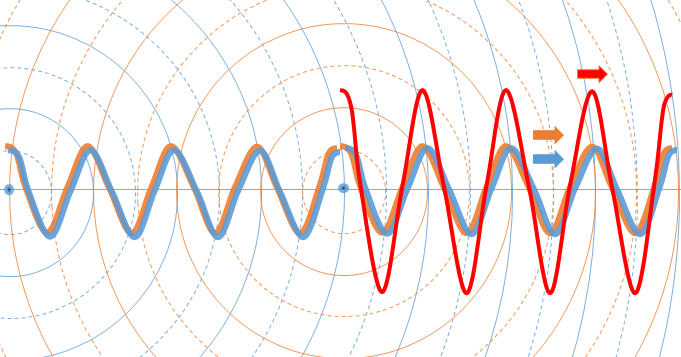
このとき2点波源の間が波長 $\lambda$ の整数倍であれば、波源右外側の波の位相が揃います。
したがってここでは強め合う波ができます。
しかし、青の波もオレンジの波も波源右外側では同じ右方向に進行するので定常波にはなりません。
強めあったまま赤い波が右へ移動して行きます。
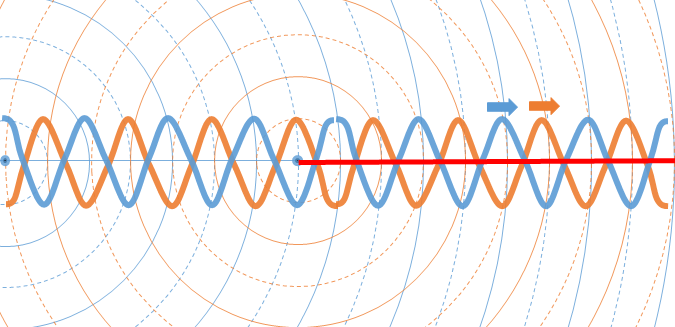
次に、2点波源の間が波長 $\lambda$ の整数倍+半波長($\lambda+\dfrac{1}{2}\lambda$)、であれば波源右外側の波の位相は逆転します。
このとき、波源右外側の波の位相はいつも逆位相ですから、この場合はずっと打ち消しあったままになります。
図の赤線が観測されます。






































コメント