断熱自由膨張とポアソンの法則
断熱自由膨張しても気体温度は変化せず、ポアソンの法則も成り立ちません。
ポアソンの法則 $pV^{\gamma}=一定$ または、$TV^{\gamma-1}=一定$
ただし、$\gamma=\dfrac{C_p}{C_V}$
ポアソンの法則
ポアソンの法則では、断熱過程において、 $pV^{\gamma}=一定$ あるいは、$TV^{\gamma-1}=一定$ が成り立ちます。ただしこの場合、準静的変化をしていることが条件です。
つまり、急激な変化の場合は成り立たない・・ということです。
準静的変化とは、変化の過程において
十分ゆっくりに変化させるような場合です。
ポアソンの法則については、次の記事を参照してください。
断熱自由膨張
断熱自由膨張とは、断熱過程において、図に示すように気体分子の体積が広がるような現象をいいます。
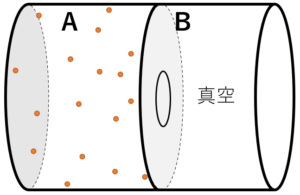
内部を A・B の 2 つに仕切った断熱容器を用意し、片方 A に気体を封入します。
一方の B は真空です。
次に、仕切りをあけて気体が自由に B に広がれるようにします。
このとき, B は真空なので A の粒子が B に移動する時の気体のする仕事 $W’$ は $0$ です。
そこで、熱力学第1法則を考えてやると、断熱過程であることから $Q=0$ なので、
\begin{eqnarray}
Q&=&\Delta U+W’ \\\\
0&=&\Delta U +0\\\\
\end{eqnarray}
より、$\Delta U=0$ となり、
断熱自由膨張のときの気体の温度低下（内部エネルギーの減少）はありません。
高校の熱力学の教科書では、普通、断熱変化において
気体が外部に対して仕事をすると、その分エネルギーが減少し、
気体の内部エネルギーが減少します。
$Q=0=\Delta U +W’$ において
$W’>0$ であるから、$\Delta U<0$ です。
そのため、気体の温度が下がります。
断熱自由膨張では、一見常識と矛盾するようですが、相手が真空の時に膨張しても、気体温度は低下しない（内部エネルギーは減少しない）ということになります。
たとえて言うなら、
断熱自由膨張は「のれんに腕押し」「ぬかにくぎ打ち」
（古いですか？）ということです。
相手が真空なので
押してもおなかが減らない（エネルギーが減少しない）のです。
注意
断熱自由膨張では、
ポアソンの法則による式 $pV^{\gamma}$ = 一定 あるいは $TV^{\gamma-1}$ = 一定 の式は成り立ちませんただし、$\gamma=\dfrac{C_p}{C_V}$
断熱自由膨張では、体積は変化しているが温度は変化していません。従って、断熱自由膨張ではポアソンの関係式 $TV^{\gamma-1}=一定$ が一定にはならず、成り立っていないことがわかります。
ポアソンの式の導出過程で、微小変化を考えているので、気体が真空に対して急激に膨張するような変化に対しては成り立たないのです。
コメント
急速に…というのは語弊があると思いますが。
例えば、スプレー缶から勢いよく中身を噴射しても温度は下がります。
また、逆の変化である断熱圧縮も急速であれば温度変化がおこらないのか？
という疑問も生じてきます。
圧縮発火装置などは急速にピストンを押し込まないと火が付かないですね。
ご指摘ありがとうございます。
>例えば、スプレー缶から勢いよく中身を噴射しても温度は下がります。
これはその通りと思いますし、断熱圧縮をすれば温度は上がるという認識です。
私が、どこかで誤解を生じさせるような記述をした可能性があります。
すみませんが、どのあたりの記述でしょうか。お知らせいただけると幸いです。
自由膨張するとき，「受入側が真空なので仕事をしない」はホントでしょうか?
受入側容器が真空なのは，初めの一瞬だけで，あとは気体が入っています。
「自由膨張で温度は変わらない」と言われています。その説明として，ポアソンの式が成り立たない，とご説明されていますが，ホントかしら?
確かに，自由膨張で圧力と温度ともに平衡した状態になれば，初めの温度と同じになります。
圧力平衡は気体の移動なので短時間で成立しますが，温度平衡は連結管を介した熱移動なため，長時間かかります。中間段階として「圧力は平衡したが温度は平衡しない」状態ができます。
送出側(A)は断熱膨張で温度が下がる。噴流の運動エネルギーとして運ばれたエネルギーが熱になって，受入側(B)は温度が上がる。この状態で，まず圧力が平衡する。
その後，温度が等しくなるまで連結管を通した熱交換がゆっくり起きる。
その結果として，初めと同じ温度になる。
がホントに起きている現象ではないでしょうか。
おっしゃるとおりかと
>自由膨張するとき，「受入側が真空なので仕事をしない」はホントでしょうか?
>受入側容器が真空なのは，初めの一瞬だけで，あとは気体が入っています。
しかし端的に申せば、
系全体（容器A+B）を一つのシステムと見なした場合、ピストンのように「外部の何か」を押し返してエネルギーを外に排出しているわけではありません。内部でエネルギーが移動しているだけなので、まあ系全体が外部へなした仕事 W は 0 としてよいのでのではないでしょうか