終端速度
抵抗を受ける運動について
スポーツカーは一般に、車高の低いすらっとした形をしています。
まちがっても、ダンプカーのような恰好はしていません。
これはなぜでしょうか?
スポーツカーは空気の抵抗を、極限まで減らす努力をしているのだということですね。

余談ですが、私たちの多くは、なぜスポーツカーを「かっこいい」と感じるのでしょうか?
別にダンプカーを「かっこいい」、と感じても何ら矛盾はないと思うのです。
(ダンプカーをスポーツカーよりも、かっこいい感じる人も、少数いると思いますが)
あ、これは私の疑問です。今のところ答えは思いつきません。
スポーツカーもダンプカーも、低速でノロノロ走っているときには、それほど空気抵抗に違いがあるとは思えません。
しかし、高速になってくると、がぜん大きな違いが生じているはずです。
それは、走る車から手を出してみれば、車が速く走る時のほうが手に感じる「風のいきおい」が大きく感じられることからも明らかです。
空気抵抗
空気抵抗は、運動する速さを $v$ とすると、$v$ に比例することがわかっています。補足
よって空気抵抗 $R$ とすると、$R=kv$ という式になります。
$k$ は比例定数です。(つまり、物体の形状などにより違います)
終端速度
では、空気抵抗を受けて落下する物体について考えます。
物体の質量を $m$ 、加速度 $a$ とすると、運動方程式は $ma=F$ より、
$$ma=mg-kv$$
となります。
注意すべきは、これは落体の運動ですが、加速度は一定にはなりません。
だんだん減少して、最後は加速度 $0$ になります。
また、抵抗力は $kv$ ですから、抵抗力は、物体が落下して速度が上がるにつれ大きくなります。
そうすると、ついに抵抗力と重力がつり合うところまで、空気抵抗が大きくなります。
このとき、運動方程式は、$mg-kv$ が $0$ になることから、
$$ma=mg-kv=0$$
となり、加速度は $0$ 、そして $ mg-kv=0 $ から、$ v=\dfrac{mg}{k} $ です。
そして、これがこの落体の最高速度となります。
このときの速度を、終端速度 $ v_t $ と呼びます。
$$ v_t=\dfrac{mg}{k} $$
雨の違い
この結果から、終端速度は、質量 $m$ が大きいほど大きくなる、ということがわかります。
すなわち、大粒の雨は「バチバチ」と降り、細かい雨は「しとしと」降る、というわけです。
$v-t$ グラフはどうなるのか
では、$v-t$ グラフを描いてみましょう。
物体が空気抵抗を受けながら落下するときのグラフは、加速度が変化するため、直線にはなりません。
\begin{eqnarray}
ma&=&mg-kv\\\\
m\dfrac{dv}{dt}&=&mg-kv\\\\
\dfrac{dv}{v-\frac{mg}{k}}&=&-\dfrac{k}{m}dt\\\\
\int{\dfrac{dv}{v-\frac{mg}{k}}}&=&-\int{\dfrac{k}{m}dt}\\\\
\log{\left|v-\dfrac{mg}{k}\right|}&=&-\dfrac{k}{m}t+C_0\:\:\:\:\:\:\:\:\:(C_0:定数)\\\\
\left|v-\dfrac{mg}{k}\right|&=&e^{-\frac{k}{m}t+C_0}\\\\
v-\dfrac{mg}{k}&=&\pm e^{-\frac{k}{m}t+C_0}\\\\
v-\dfrac{mg}{k}&=&\pm e^{C_0}e^{-\frac{k}{m}t}\\\\
v-\dfrac{mg}{k}&=&Ce^{-\frac{k}{m}t}\:\:\:\:\:\:\:\:\:(C=\pm e^{C_0})\\\\
v&=&Ce^{-\frac{k}{m}t}+\frac{mg}{k}\\\\
\end{eqnarray}
ここで、$t=0$ で、$v=0$ だから、
\begin{eqnarray}
v&=&Ce^{-\frac{k}{m}t}+\frac{mg}{k}\\\\
0&=&Ce^{-\frac{k}{m}\times 0}+\frac{mg}{k}\\\\
0&=&C+\dfrac{mg}{k}\\\\
\end{eqnarray}
より、 $C=-\dfrac{mg}{k}$ です。
ゆえに、
\begin{eqnarray}
v&=&-\dfrac{mg}{k}e^{-\frac{k}{m}t}+\dfrac{mg}{k}\\\\
&=&\dfrac{mg}{k}\left(1-e^{-\frac{k}{m}t}\right)\\\\
v&=&\dfrac{mg}{k}\left(1-\dfrac{1}{e^{\frac{k}{m}t}}\right)
\end{eqnarray}
このとき、$t \rightarrow \infty$ で、$v \rightarrow \dfrac{mg}{k}$ となることがわかります。
これを $v-t$ グラフにすると、次のようになります。 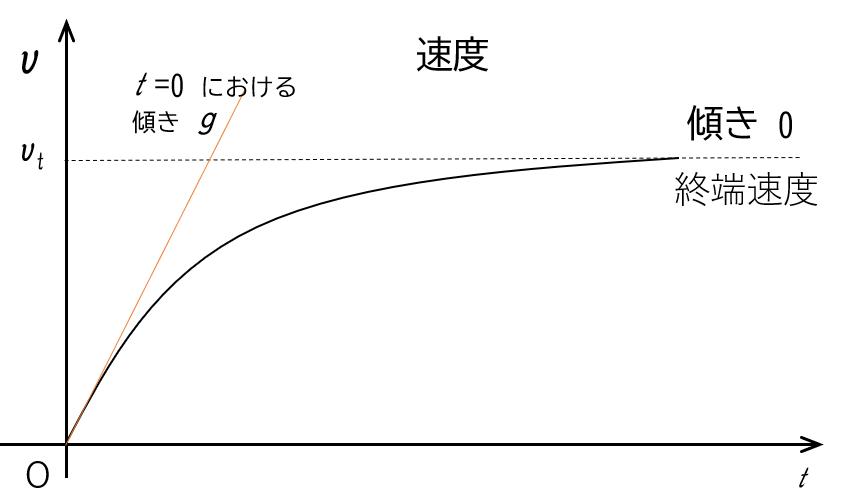
加速度は、$v-t$ グラフの傾きです。
加速度を求めてみると、
\begin{eqnarray}
a&=&\dfrac{d}{dt}v\\\\
&=&\dfrac{d}{dt}\left[\dfrac{mg}{k}\left(1-e^{-\frac{k}{m}t}\right)\right]\\\\
&=&ge^{-\frac{k}{m}t}\\\\
&=&g\dfrac{1}{e^{\frac{k}{m}t}}\\\\
\end{eqnarray}
よって、加速度の大きさは、時間とともにだんだん減少していくことがわかります。
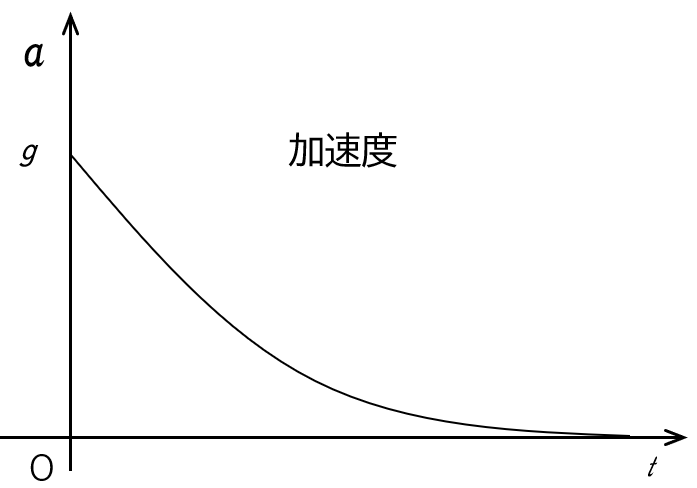

このとき、$t \rightarrow \infty$ で、$a \rightarrow 0$ となることがわかります。
これは、終端速度に達したとき、 $v-t$ グラフの傾きが $0$ 、
つまり $t$ 軸に平行になる、ということを示しています。

$t=0$ においては、$a=g$ です。
$v-t$ グラフにおいては、$t=0$ におけるグラフの接線の傾きが $g$ であることを示しています。
補足
空気抵抗の大きさと物体の速さの関係は、物体の速さが比較的小さいときは速さに比例 ( $kv$ ) し、速さが大きいときは、速さの二乗に比例する ( $kv^2$ ) ことがわかっています。




































コメント