相対速度とともに相対加速度を考えれば、より応用範囲が広がります。
相対速度や相対加速度の便利なところは観測者を止めることができる点です。
また、v-tグラフを使えば簡単になることも多くあります。
物理のエッセンス力学編 14番
問題
長さ $125\:\mathrm{m}$ の列車と、自動車(大きさが無視できる)の競争です。
図のようにスタートしますが、列車と自動車は表のように、初速度と加速度がわかっています。
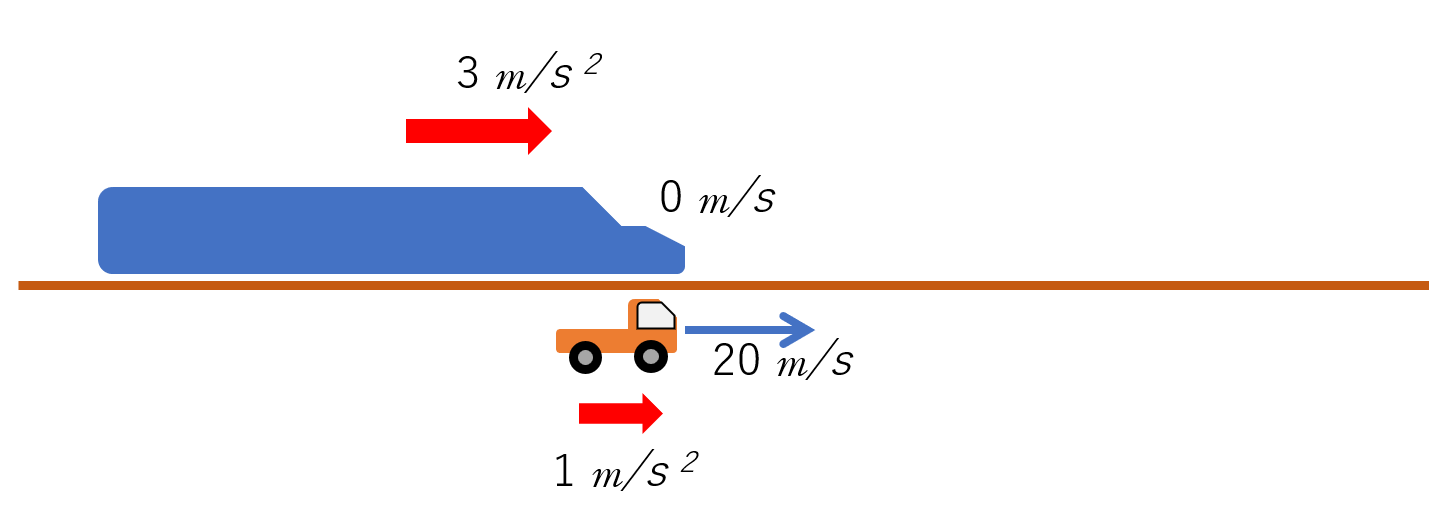
| 初速度 | 加速度 | |
| 列車 | $0\:\mathrm{m/s}$ | $3\:\mathrm{m/s^2}$ |
| 自動車 | $20\:\mathrm{m/s}$ | $1\:\mathrm{m/s^2}$ |
- このとき、
- 列車と車の、前方への最大車間距離を求めましょう。
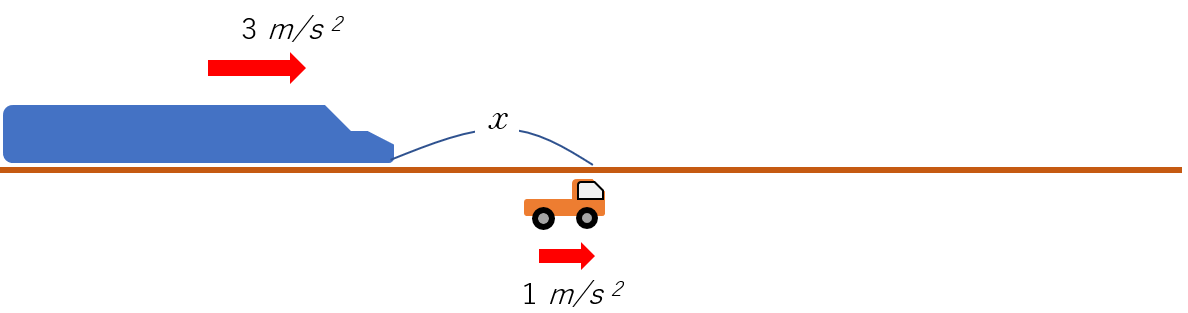
- 列車が車を、完全に抜き去るのに要する時間 を求めましょう。
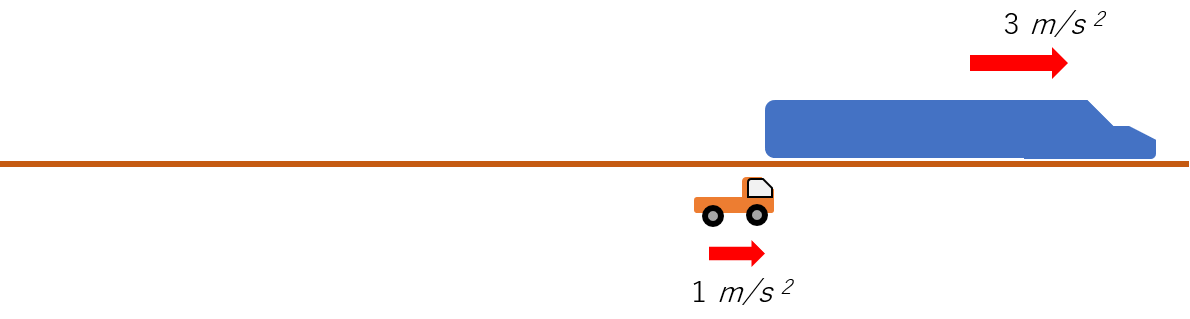
それでは、まず相対加速度から考えていきます。
相対加速度
相対速度と同じように、加速度も相対加速度を考えることができます。

相対加速度が成り立つ理由
Aが速度 $v_A$ 、Bが速度 $v_B$ で運動しているとき、
Bに対するAの相対速度 $v_{BA}$ は、
$$v_{BA}=v_A-v_B$$
で示されます。
相対速度の式の両辺を、時間微分 $\dfrac{\mathrm{d}}{\mathrm{dt}}$ します。
もうちょっとくわしく・・は補足へ
$$\dfrac{\mathrm{d}}{\mathrm{dt}}v_{BA}=\dfrac{\mathrm{d}}{\mathrm{dt}}v_A-\dfrac{\mathrm{d}}{\mathrm{dt}}v_B$$
ここで 加速度を、それぞれ $a_{BA}$ 、$a_A$ 、$a_B$ とすると、$a=\dfrac{\mathrm{d}v}{\mathrm{dt}}$ なので、
$$a_{BA}=a_A-a_B$$
ですね。
したがって、相対速度と同じように、加速度ベクトルの引き算をすればよいことになります。
この問題は相対加速度を考えることで非常に容易になります。
列車からと車の車間距離
列車から見た自動車の相対加速度 $a_{TA}$ は、列車の加速度 $a_T$ 、自動車の加速度を $a_A$ とすれば、
$a_{TA}= a_A-a_T=1-3=-2\:\mathrm{m/s^2}$
です。
よって、列車から見ると自動車は相対的な初速度 $20\:\mathrm{m/s}$ で出発し、相対加速度 $-2\:\mathrm{m/s^2}$ で運動しているように見えます。

相対初速度
$v_{0TA}=v_{0A}-v_{0T}=20-0=20\:\mathrm{m/s}$
つまり、列車は静止している・・・ということです。 ← これ大事
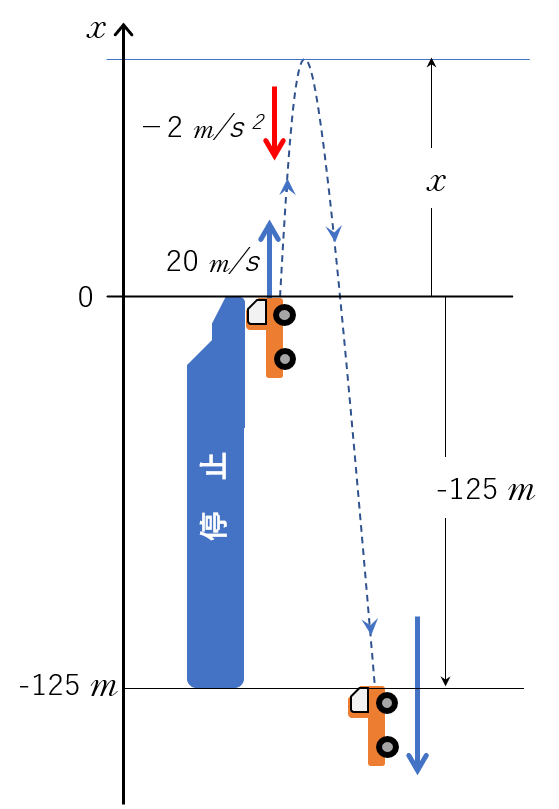
列車の人から見ると、自動車が鉛直投射の球のように、飛び出して戻ってくるように見えます。
ちなみに、相対加速度は、 $-2\:\mathrm{m/s^2}$ で一定です。
次の図と同じイメージです。
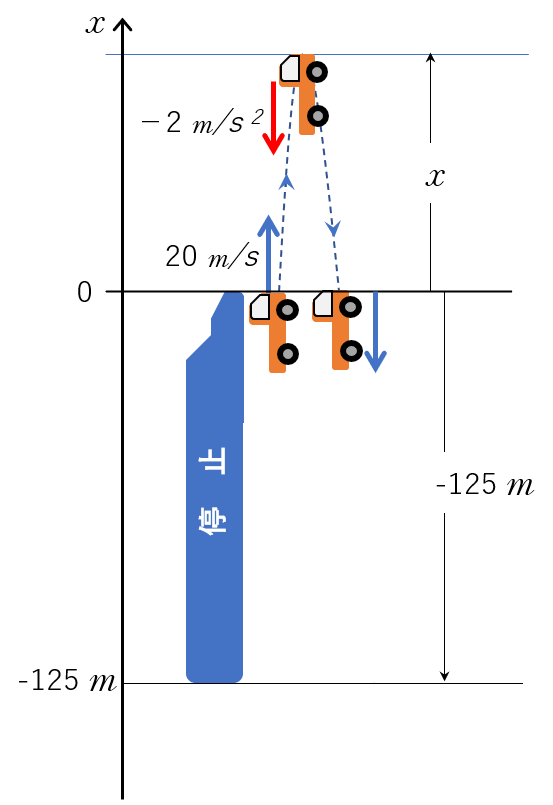
ということは、$v^2-v_0^2=2ax$ において、$a=-2\:\mathrm{m/s^2}$ 、$v_0=20\:\mathrm{m/s}$、 $v=0\:\mathrm{m/s}$ の時の $x$ を求めればよいことになります。
\begin{eqnarray}
v^2-v_0^2&=&2ax\\\\
0^2-20^2&=&2\times(-2)x\\\\\\
x=100\:\mathrm{m}
\end{eqnarray}
となり、答えは $100\:\mathrm{m}$ です。
$v-t$ グラフを使えば超簡単!
$v-t$ ブラフを使えば、もっと簡単に求められます。
列車を停止しているとしたときの、図のグラフで、傾きは自動車の相対加速度を示していますから、このグラフの傾きは $-2$ です。
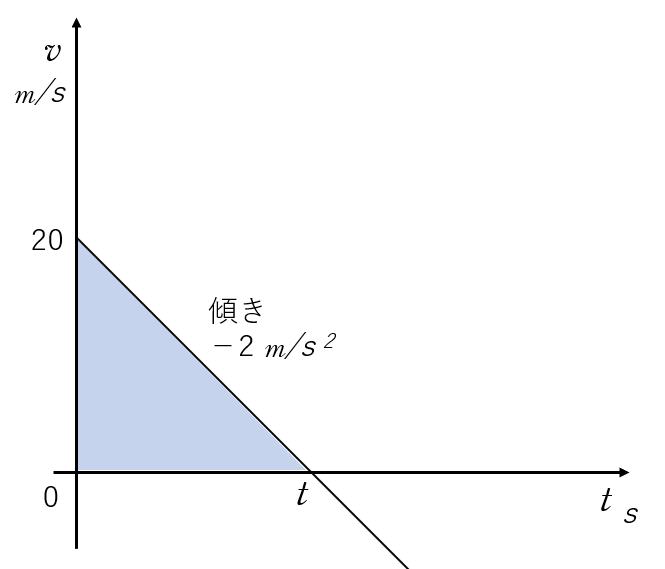
自動車の相対初速度は $20\:\mathrm{m/s}$ ですから、グラフの切片は $20$ です。
$t$ 軸を横切る時間 $t_h$ は、グラフの傾きが加速度ですから、 $\dfrac{20}{t_h}= |-2|$ より、$t_h=10$ となります。
一番離れているところは、投げ上げの最高点なので、その距離は図の三角形面積を求めればよいことになります。
したがって、$x=\dfrac{10\times 20}{2}=100 \:\mathrm{m}$ という答えになります。
$v-t$ グラフの活用については、次の記事をぜひお読みください。
列車が車を抜き去るのに要する時間
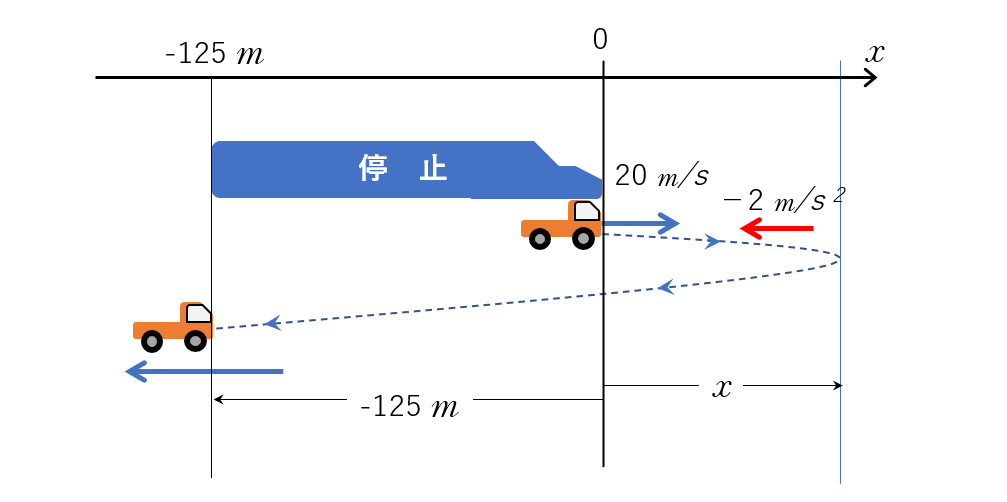
では次に、列車が自動車を抜き去るのに要する時間 $t$ を求めます。
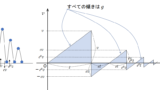
これも、先ほどと同じく、列車の視点から見ます。
そうすると、鉛直投げ上げした球が、地面のさらに下、$-125\:\mathrm{m}$ のところまで落ちる時間を求めることと同じです。(自動車の大きさは $0$ です。念のため)
相対加速度はやはり、$-2\:\mathrm{m/s^2}$ で一定です。
そのため、$x=v_0t+\dfrac{1}{2}at^2$ の式を使えば、
$$-125=20t+\dfrac{1}{2}(-2)t^2$$
を解けばおしまいです。
よって、
$$t^2-20t-125=0$$
より、
$$(t+5)(t-25)=0$$
$t= -5, \: 25 $
となり、$t>0$ であることから、答えは、$25\:\mathrm{s}$ となります。
$v-t$ グラフを使ってみると
これも $v-t$ グラフを使うことで解くことができます。
つまり、図のグラフと $t$ 軸で囲まれた面積から計算される変位量が $-125$ であればよいことになります。
$t=10$ 最高点へ、$t=20$ で元に戻ります(青の三角形は合同になる)。
よって、具体的には、$t=20$ のところから、時間 $T$ かかるして、図の台形の面積が $125$ になればよいことになります。
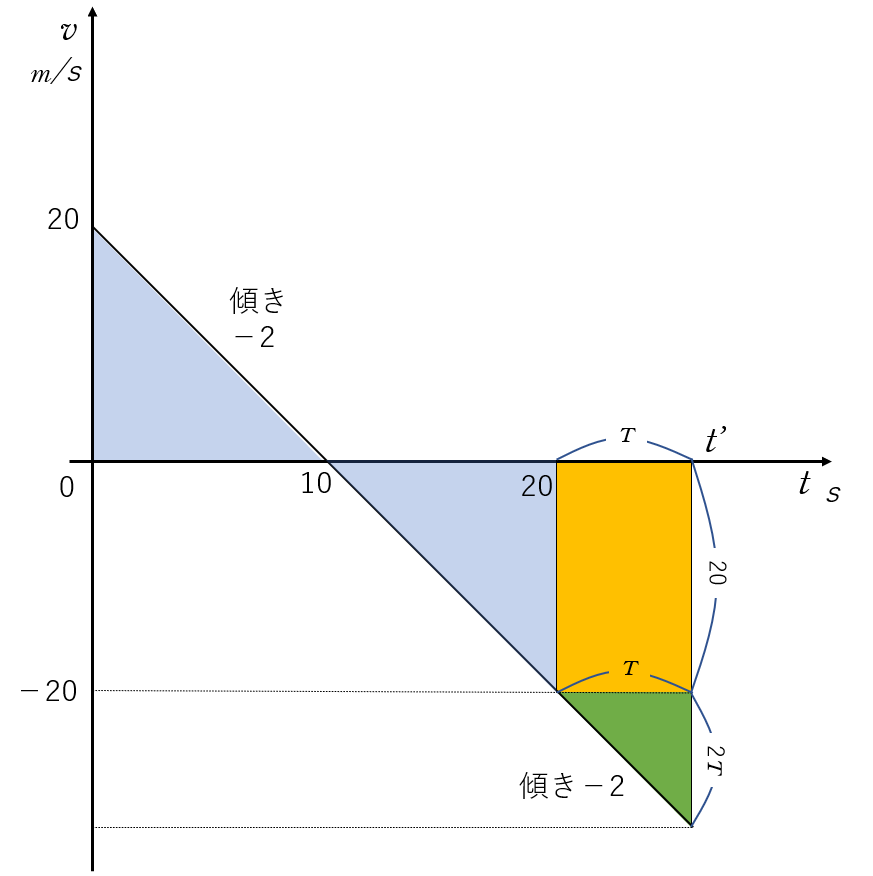
ここで、台形を四角形と三角形に分けてみると、三角形の高さは、傾きが $|-2|$ であることから、$2T$ となります。
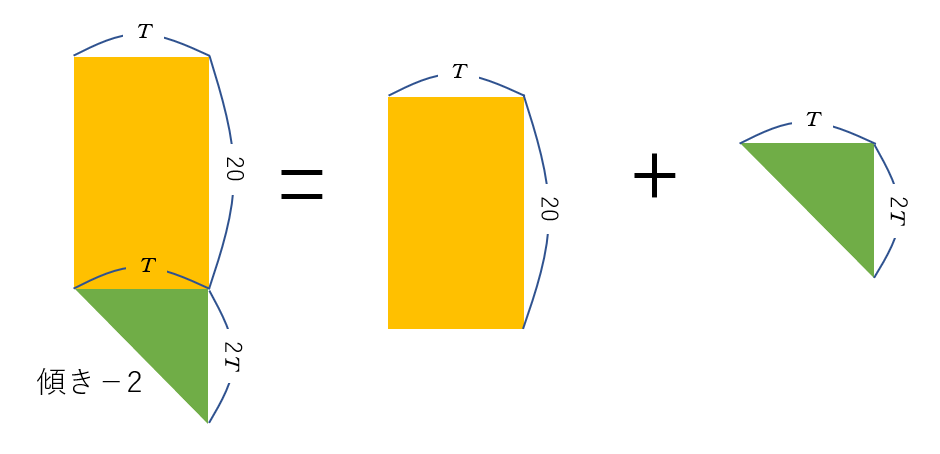
したがって、台形の面積は
$$T\times 20 + T\times (2T)=125 $$
$$(T-5)(T+25)=0$$
より、$T=5 \;,\:-25$ を得ます。
ここで $T>0$ より、$T=5$ です。
よって、最初からの時間は、$20+T=25\:\mathrm{s}$ となります。
補足
相対加速度について考えます。
物体Aの速度が、$\Delta t$ 間で $v_A(t)$ から $v_A(t+\Delta t)$ へ変化したとします。
そうすると、加速度 $a_A(t)$ は、
$a_A(t)=\dfrac{v_A(t+\Delta t)-v_A(t)}{\Delta t}\:\:\:\cdots \cdots (1)$
同様に、物体Bについて、$\Delta t$ 間で速度が $v_B(t)$ から、$v_B(t+\Delta t)$ へと変化しました。加速度 $a_B(t)$ は、
$a_B(t)=\dfrac{v_B(t+\Delta t)-v_B(t)}{\Delta t}\:\:\:\cdots \cdots (2)$
ここで、$ (1)-(2)$ としてみると、
\begin{eqnarray}
a_A(t)-a_B(t)&=&\dfrac{v_A(t+\Delta t)-v_A(t)}{\Delta t}-\dfrac{v_B(t+\Delta t)-v_B(t)}{\Delta t}\\\\
&=&\dfrac{v_A(t+\Delta t)-v_B(t+\Delta t)}{\Delta t}-\dfrac{v_A(t)-v_B(t)}{\Delta t}\\\\
\end{eqnarray}
ここで、
$v_{BA}(t)=v_A(t)-v_B(t)$
$v_{BA}(t+\Delta t)=v_A(t+\Delta t)-v_B(t+\Delta t)$
より、
\begin{eqnarray}
a_A(t)-a_B(t)&=&\dfrac{v_{BA}(t+\Delta t)}{\Delta t}-\dfrac{v_{BA}(t)}{\Delta t}\\\\
&=&\dfrac{v_{BA}(t+\Delta t)-v_{BA}(t)}{\Delta t}=a_{BA}(t)\\\\
\end{eqnarray}
$\lim \Delta t \rightarrow 0$ とすれば、以上は微分定義そのものです。
そして、相対加速度も相対速度と同様に「引けばよい」
$a_{BA}(t)=a_A(t)-a_B(t)$
ということです。引く順番には注意してください。





































コメント