合成ばね定数の求め方
動画解説
ばねを短くするとどうなるか
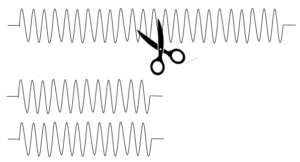
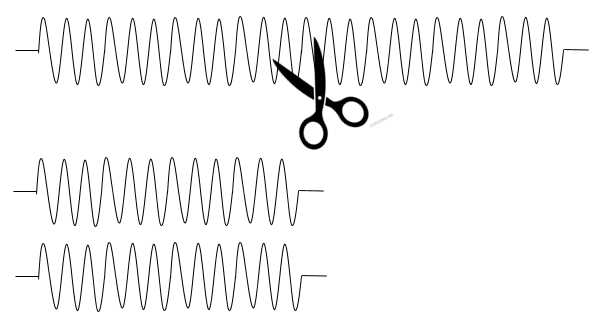
ばねを真ん中から2つに切り分けました。
さて、切って短くなったばねはどうなるでしょうか?
選択肢
-
- 固くなる
- 柔らかくなる
- 変わらない

答え
答えは 2 の「柔らかくなる」・・・ではなくて 1 の「固くなる」です。
直感的に考えれば、柔らかくなるような気がしますが・・・・。
ここで、ばねの性質について考えてみましょう。
ばね定数はご存知ですね。
ばね定数は通常、単位 [N/m] で示されるもので、ばねを 1 [m] 伸ばすために必要な力 [N] で示されます。
つまり、ばね定数が大きいと「固い」ばね、小さいと「柔らかい」ばねとなります。
さて、あるばねを 1 [m] 伸ばすことを考えます。実際問題として 1 [m] も伸ばせば、ばねは伸び切ってしまいますが、ここは思考実験ということでご勘弁を。
そのばねを半分に切ってしまうと、その半分に切った短いばねを 1 [m] だけ伸ばすのが、切られた新しいばねのばね定数です。
ということは、切られて半分の長さになったばねを 1[ m] 伸ばすのですから、切られて短くなったばねは、切られる前の2倍伸ばす必要があります。
つまり、切られる前は 50 [cm] 、50 [cm] づつ伸びればよかったのですが、それが 1 [m] まで伸ばされます。
したがって、ばねは「固く」なるのです。
フックの法則より、ばねを引く力はばねの伸びに比例します。
ばね定数の意味・・・「1 [m] だけ伸ばすのに必要な力」から考え得ると、必要な力は2倍になっていると考えられます。
そのため、ばね定数も2倍となるのです。
逆に、ばねを連結して長いばねとして扱うと、ばねは「柔らかく」なります。
なぜなら、一つ一つのばねが伸びなければならない距離は半分で済むからです。
したがって、同じばねを2つつなげると全体でのばね定数は $\dfrac{1}{2}$ となることがわかります。
ばね定数の違うばねをつなげるとどうなるのか
ばね定数 $k_1$ と $k_2$ のばねをつなげて使いましょう。
このとき、全体でのばね定数はどうなるのでしょうか?
では次の図で考えましょう。
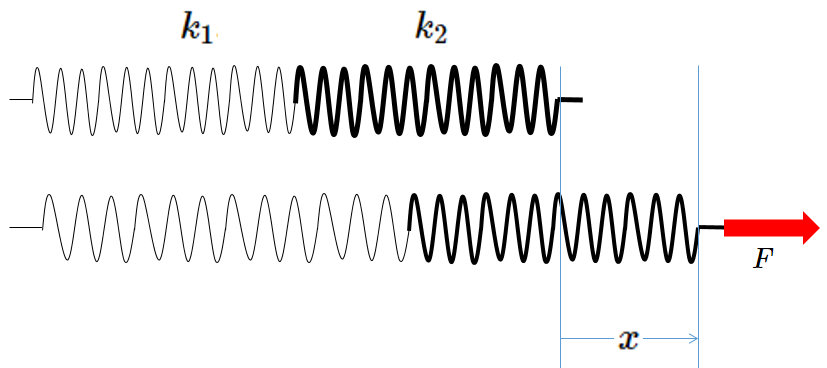
いま、つなげたばねで、ばね全体が $x$ だけ伸びているとしましょう。
そうすると、必要な力を $F$ とすると、フックの法則 $F=kx$ より、
$F=kx$
ここで、そのときのばね定数 $k_1$ と $k_2$ のばねの伸びをそれぞれ $x_1$、$x_2$ とします。
当然、$x_1+x_2=x$ です。
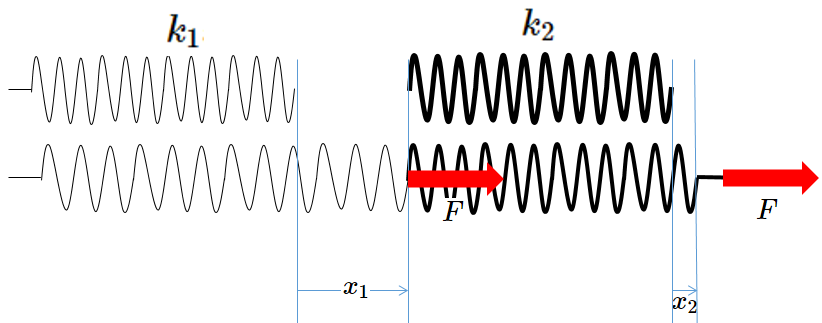
よって、
$$F=k(x_1+x_2)$$
$k_1$ と $k_2$ のばねにかかる力 $F$ はそれぞれのばねに同じだけかかりますから、

注意!
半分だけの力でよいというわけではありません
$k_1$ のばねも $k_2$ のばねも同じ力で引かれています
$F=k_1 x_1$ より、$x_1=\dfrac{F}{k_1}$
$F=k_2 x_2$ より、$x_2=\dfrac{F}{k_2}$
さて、ここで $x_1$ と $x_2$ をそれぞれ、$F=k(x_1+x_2)$ へ代入します。
$$F=k\left(\dfrac{F}{k_1}+\dfrac{F}{k_2}\right)$$
ゆえに、
$$\dfrac{1}{k}=\dfrac{1}{k_1}+\dfrac{1}{k_2}$$
これってコンデンサーの直列接続の場合の合成容量の式と同じ形ですね。
ばねを並列にしてつなげて使うとどうなるか
コンデンサーの合成容量を求める式との類似を考えると、ばねを並列接続した場合に合成ばね係数の式は、
$$k=k_1+k_2+ \cdots$$
となってほしいところです。
確かめてみましょう。
図において、ばねを $x$ だけ引き伸ばしたと考えましょう。
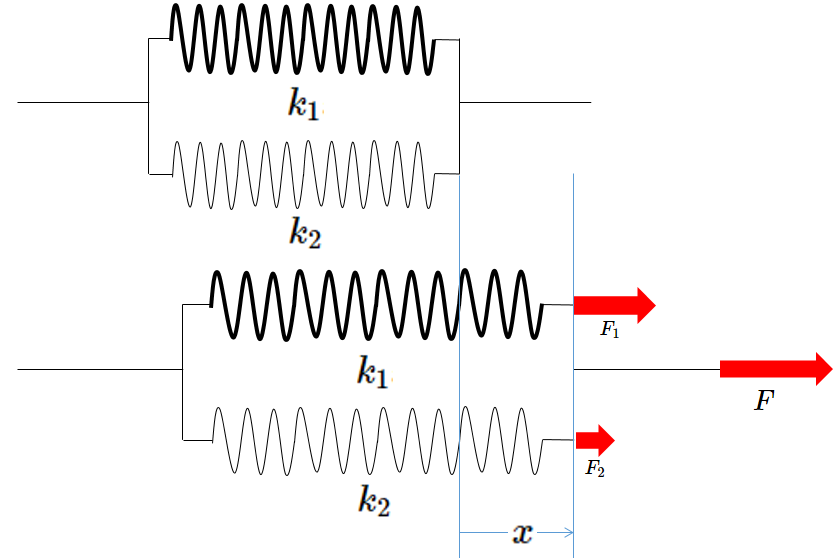
そのとき、どちらのばねも等しく $x$ 伸びています。
また、ばね定数 $k_1$、 $k_2$ のばねそれぞれにはたらく力を $F_1$、$F_2$ とします。
フックの法則から、
$$F_1=k_1x$$
$$F_2=k_2x$$
です。
力の関係から、$F=F_1+F_2$ であるので、それぞれ代入します。
\begin{eqnarray}
F&=&F_1+F_2\\
&=&k_1x+k_2x\\
&=&(k_1+k_2)x\\
&=&kx
\end{eqnarray}
したがって、合成容量 $k$ は
$$k=k_1+k_2$$
となります。
オススメの問題集参考書は






































コメント