物理のエッセンス 原子 7番

物理のエッセンス 原子 7番

物理のエッセンス原子編の7番について解説します。

まずは、基本事項のおさらいです。

• 光速 $c$ と振動数 $\nu$ 波長 $\lambda$ の関係　　$c=\nu\lambda$
• 光子エネルギー $E$　　$E=h\nu$
• 光子運動量 $p$　　$p=\dfrac{E}{c}=\dfrac{h\nu}{c}=\dfrac{h}{\lambda}$
• 運動量と力積の関係　　$p_0+I=p$
• エネルギーの原理　　$E_0+W=E$

どんな問題？

光子が壁にぶつかって吸収される場合と、完全に反射する場合の光の板に及ぼす力を求めます。

これって、光子ロケットの原理ですね。

光子ロケットとは、光源から受ける光圧によって推進力を得るもので、加速度は小さいけれど最高速度は大きいというヤツです。

光子が板に吸収される場合

まず、光子が板に完全に吸収される場合を考えましょう。

光子1個について、運動量 $p$ と力積 $I$ の関係、$p_0+I=p$ を考えます。

この場合、光子が運動量 $\dfrac{h\nu}{c}$ で飛んできて、壁に吸収されて運動量 $0$ となります。

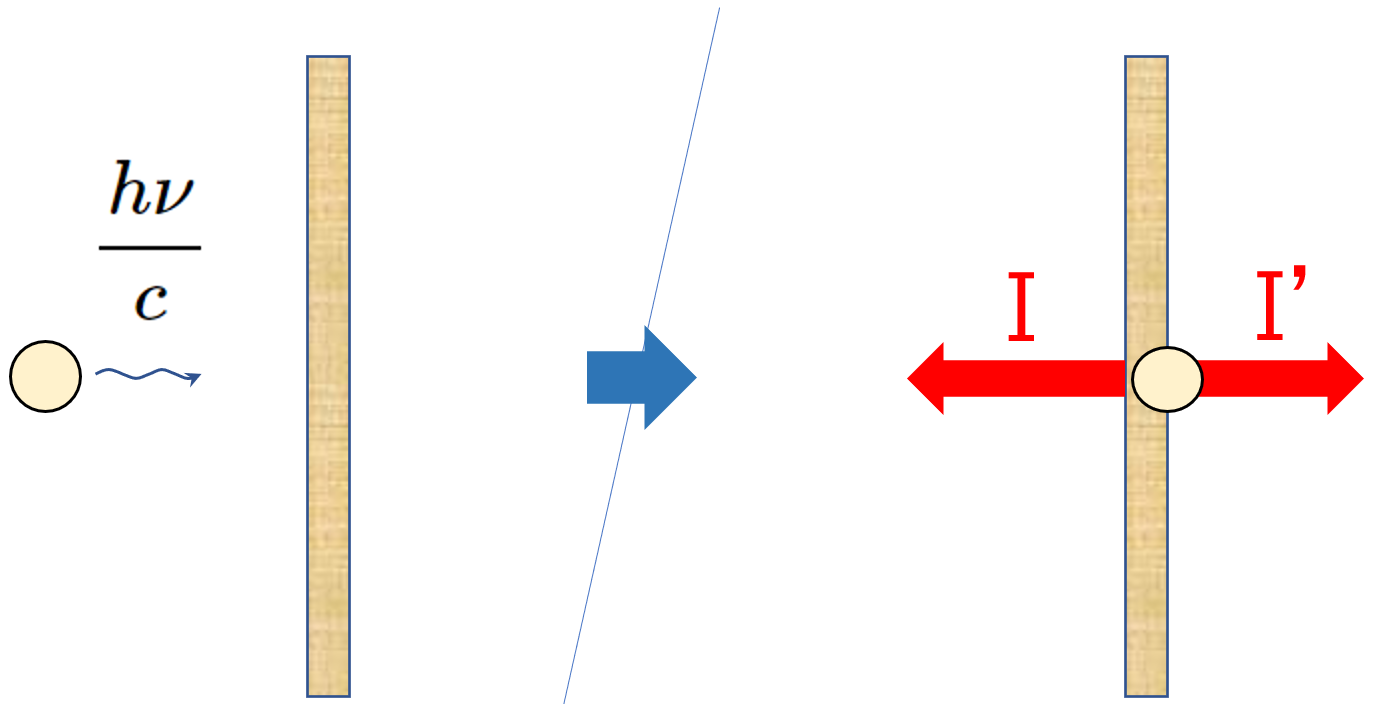
図の右向きを正として、運動量 $p_0=\dfrac{E}{c}=\dfrac{h\nu}{c}$ 、$p=0$ ですから、 $p_0+I=p$ より、

$$\dfrac{h\nu}{c}+I=0$$

この式から、$I=-\dfrac{h\nu}{c}$ ですが、この $I$ は光子の受ける力積を示しています。

つまり光子は板から図の左向きに、大きさ $I$ の力積を受けてその運動量が $0$ になった、というわけです。

ここで、壁は作用反作用の法則より、光子1個が板に吸収されるときに $I’=\dfrac{h\nu}{c}$ の力積を受けます。（図の右向きを正とする）

今、光子1個のエネルギー $E$ は $E=h\nu$ であるから、毎秒 $L\:[J]$ のエネルギーを受けているときの1秒間に壁に当たる光子数を $N$ とすると、

\begin{eqnarray}
N&=&\dfrac{L}{E}\\\\
&=&\dfrac{L}{h\nu}\\\\
\end{eqnarray}

したがって、力積 $I$ の式 $I=ft$ より、（$f$ は力、$t$ は時間）1秒を考えると、壁が受ける（平均の）力 $f$ は、

\begin{eqnarray}
I=f\times 1&=&N\dfrac{h\nu}{c}\\\\
&=&\dfrac{L}{h\nu}\dfrac{h\nu}{c}\\\\
f&=&\dfrac{L}{c}
\end{eqnarray}

光子が反射される場合

反射される場合も、光子が吸収される場合と同様に考えます。

 $p_0+I=p$ より、 図の右向きを正として、運動量 $p_0=\dfrac{E}{c}=\dfrac{h\nu}{c}$ 、$p=-\dfrac{h\nu}{c}$ ですから、

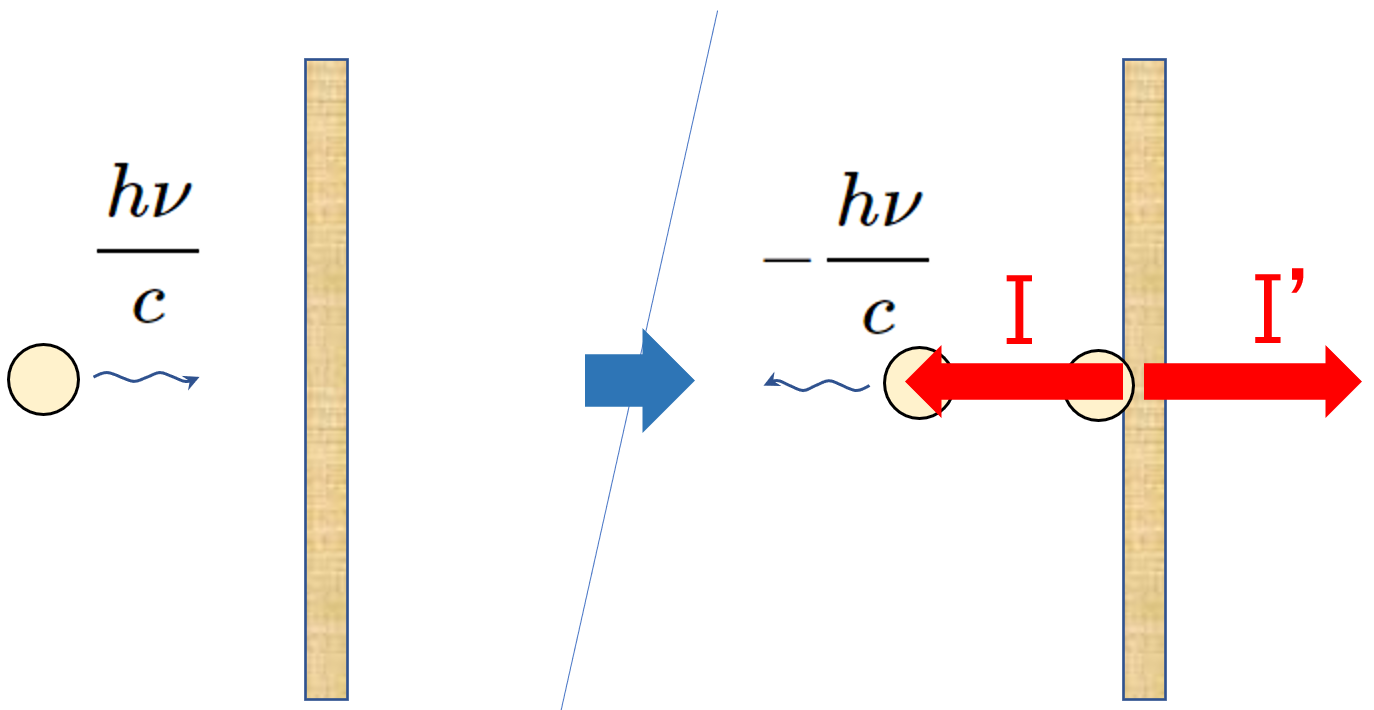
 $$p_0+I=p$$

$$\dfrac{h\nu}{c}+I=-\dfrac{h\nu}{c}$$

より、$I=-2\dfrac{h\nu}{c}$ ですが、この $I$ は光子の受ける力積を示しています。 

つまり、図の右を正として、1個の光子は板から $I=-2\dfrac{h\nu}{c}$ の力積を受けることにより運動量が、$\dfrac{h\nu}{c}$ から、$-\dfrac{h\nu}{c}$ に変化したのですね。

作用反作用の法則から、壁は光子1個が板で反射されるときに $I’=2\dfrac{h\nu}{c}$ の力積を図の右側に受けます。

また、1秒間に壁に当たる光子数 $N=\dfrac{L}{h\nu}$ です。

したがって、力積 $I$ の式 $I=ft$ より、（$f$ は力、$t$ は時間）1秒を考えると、壁が受ける（平均の）力 $f$ は、

\begin{eqnarray}
I=f\times 1&=&N\dfrac{2h\nu}{c}\\\\
&=&\dfrac{L}{h\nu}\dfrac{2h\nu}{c}\\\\
f&=&\dfrac{2L}{c}
\end{eqnarray}

エッセンスの後は良問・名問をおススメします。

AmazonAmazonAmazon Amazon