電流の式 I=envS 導出
電流の式 $I=envS$ 導出を考えます。
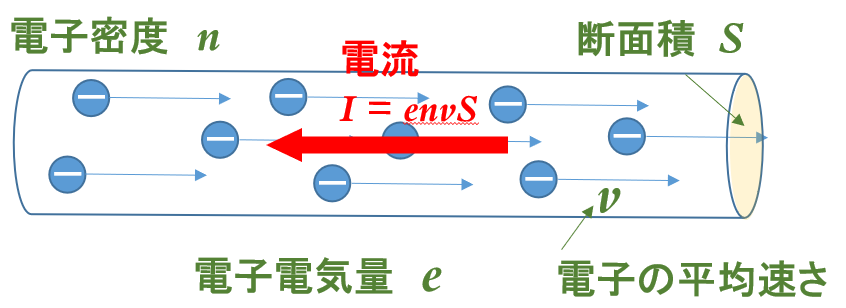
電流 $I$ 、電子電気量 $e$ 、電子密度 $n$ 、電子平均速さ $v$ 、導線の断面積 $S$ とします。
それぞれの意味については、この記事でもおいおい解説をしていきます。

覚え方
私 ($I$) はブスネ ($vSne$) 、$I=envS$ でいかがでしょうか。
それでは、電流とはなんだっけ?・・というところから始めましょう。
電流の定義
まずは電流の定義です。
電流 $I$ は単位時間(1秒間として良いでしょう)あたりに流れる電気量のことです。
今、$t$ 秒間で $Q$ だけの電気量が流れたとすると、電流 $I$ は、$I=\dfrac{Q}{t}$ です。
導体の断⾯を通過する電気量が $1\:[\mathrm{s}]$ 秒間に $1\:[\mathrm{c}]$ であるとき、その電流を $1\:[\mathrm{A}]$ と定義しています。
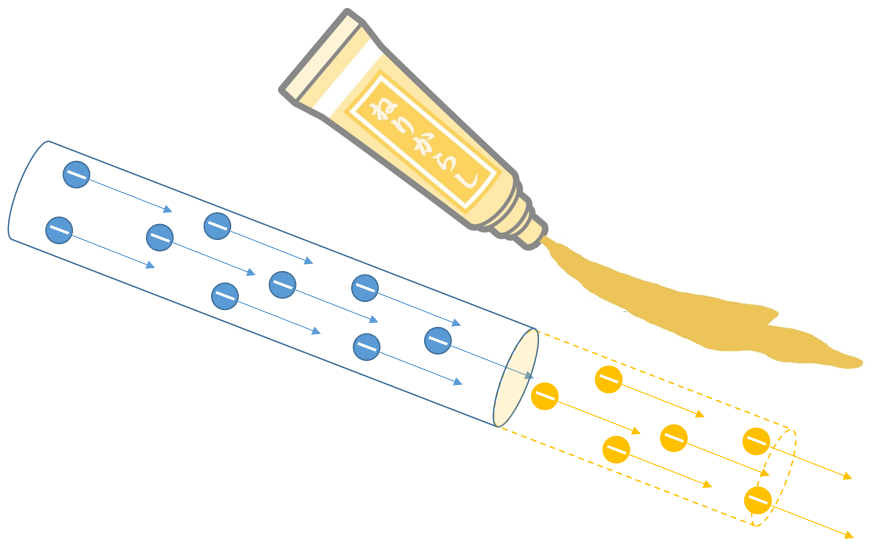
なんだか難しそうな話ですが、チューブからしを手で押し出すとき、出てくるからしを想像してもらいましょう。そのとき、「からし(電子)の出るいきおい」を定式化したものです。
図を参照してください。
つまり、 $1\:[s]$ 間にどれだけからし(電子)がでるのか、ということです。
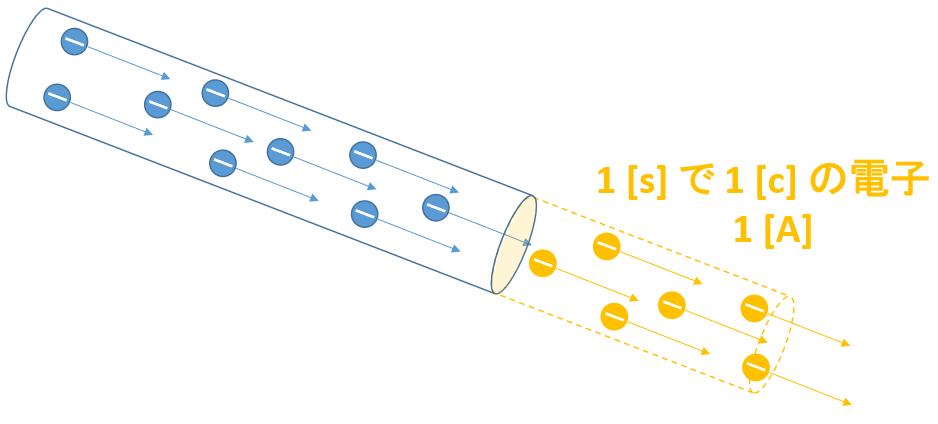
次の図にあるように、導線から電子が $1\:[\mathrm{s}]$ に $1\:[\mathrm{c}]$ 分だけ押し出されたとき、そのときの電流は $1\:[\mathrm{A}]$ であるとします。
$1\:[\mathrm{A}] = 1\:[\mathrm{c/s}]$

ここで、電子一個の電気量(電気素量)は、
$e=-1.60\times 10^{-19}\:[\mathrm{c}]$ です。
また、電子電荷は負なので、
電流は電子の動きとは逆の方向になります。
つまり、電流 $I$ は、単位時間あたりの移動する電気量を求めているのです。
したがって、時間 $t$ の間に $Q$ の電気量が流れたとすると、電流 $I$ は、
$$I=\dfrac{Q}{t}$$
と示され、電流単位は $[\mathrm{A}]=[\mathrm{c/s}]$ と示されます。
電子1個の電気量(電気素量)は、$e=-1.60\times 10^{-19}\:[\mathrm{c}]$ です。
$1\:[\mathrm{s}]$ 秒間に押し出されたすべての電気量 $Q$ を計算するには、$1\:[\mathrm{s}]$ 秒間に押し出された電子の総数 $N$ を求めて、電気素量 $|e|$ をかけることで得られます。
つまり、$Q=eN$ ですね。
そして、電流 $I$ は $Q$ を時間(ここでは$1\:[\mathrm{s}]$ )で割る $I=\dfrac{Q}{t}$ ことで得られます。
よって、
$$I=\dfrac{Q}{t}=\dfrac{eN}{1} \:\:\:\: \cdots\cdots(1)$$
です。
押し出された電子の総数 $N$ を求める
ここで、導線の断面の面積を $S$ 、電子の移動平均速さを $v$ とし、$1\:[\mathrm{s}]$ を考えてみましょう。

もちろん、電子の速さはまちまちですが、
ここでは平均の速さ $v$ を考えます。
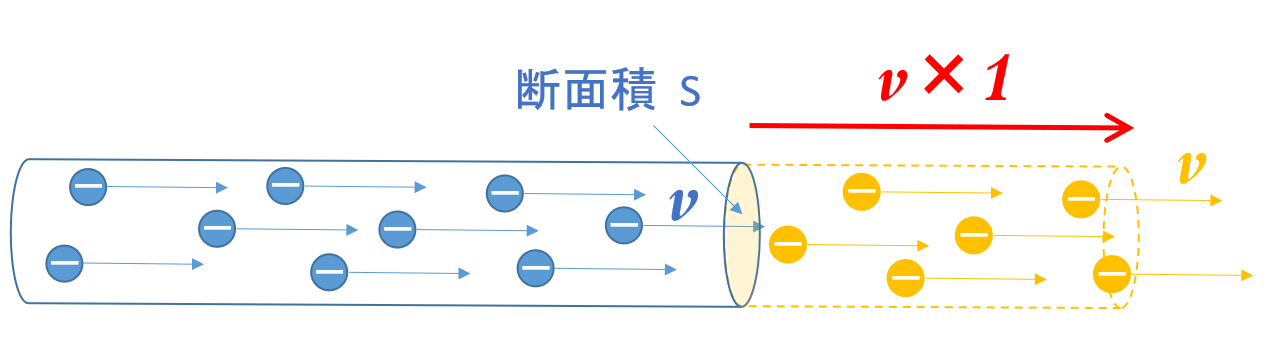
となると、$1\:[\mathrm{s}]$ では $v\times 1$ の長さに相当するだけの電子が移動しているはずです(図)。
そうすると、次の図からわかるように、$1\:[\mathrm{s}]$ 間で押し出された電子の体積 $V$ は、
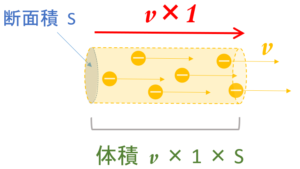
$V=(v\times 1)\times S$
となります。
電子密度
次に電子密度 $n$ を考えます。
電子密度というと何やら難しそうですが、要は、$1\:[\mathrm{m^3}]$(単位体積) にある電子の数のことです。これは物質により違う値を持ちます。
$n$ は、電子総数 $N$ を体積 $V$ で割ることによって求めることができます。
つまり、$n=\dfrac{N}{V}$ ですね。
これから、$N=nV$ となります。
先ほど求めた、$V=(v\times 1) \times S$ より、
$$N=nV=n \times {(v\times 1) \times S}=nvS$$
電流 $I$ を求める
では、電流 $I$ は?
それは式 (1) より、$I=\dfrac{Q}{t}=\dfrac{eN}{1} $ であるから、$N=nvS$ を代入して、
\begin{eqnarray}
I&=&\dfrac{Q}{t}\\\\
&=&\dfrac{eN}{1}\\\\
&=&\dfrac{envS}{1}\\\\
I&=&envS
\end{eqnarray}
これにより、$I=envS $ となることがわかります。
時間 $t$ では?
今回は $1\:[\mathrm{s}]$ で考えましたが、 $t\:[\mathrm{s}]$ 間で考えても同じことです。
$t\:[\mathrm{s}]$ で電子は $t\:[\mathrm{s}]$ で $(v\times t)$ だけ進むので、先ほどの式で、$(v\times 1)$ のかわりに、$(v\times t)$ とするだけです。
つまり、$N=n\times(v\times t)\times S=nvtS $ となるので、
\begin{eqnarray}
I&=&\dfrac{Q}{t}\\\\
&=&\dfrac{eN}{t}\\\\
&=&\dfrac{envtS}{t}\\\\
I&=&envS
\end{eqnarray}
となり、当然同じ結果になります。





































コメント