交流の発生 交流の基礎1

電磁気の記事は次を参照してください。

交流電源について
交流の発生のため、図のような装置を考えることにします。
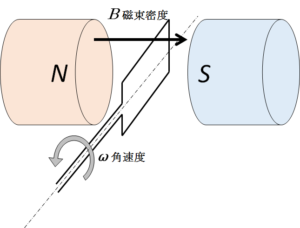
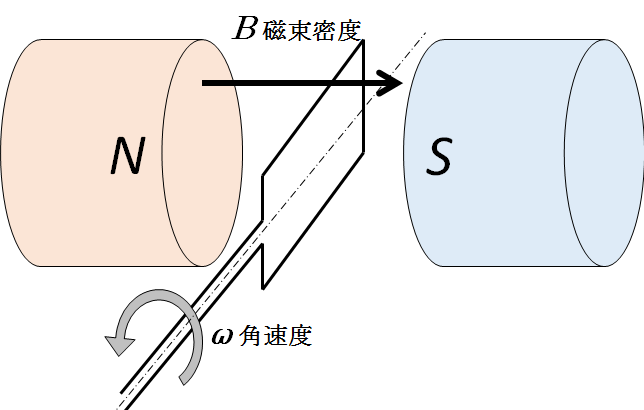
磁石を水平対向させ、コイルを角速度 $\omega$ で外部動力(例えば手など)で回転させることで誘導起電力を得ます。(注意:これはモーターではありませんので勝手に動きません。外部からエネルギーを与える必要があります。)
このとき、磁束 $\Phi$ 、磁束密度 $B$ 、コイルの磁場内の面積 $S$ とすると、
$\Phi=BS\:\cdots\cdots (1)$
が成り立ちます。
次の図は真横から見た図で、この磁石のつくる磁場を $B$ で一様であるとします。
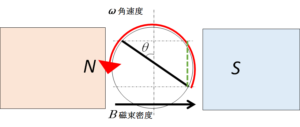
図のコイルの場合、時間とともに磁束に対する断面積 $S’$ が、 $S’=S\cos \theta$ のように変化します。
ただし、$\theta$ は図の回転角を示しています。
このとき、回転角 $\theta$ は、角速度 $\omega$ と時間 $t$ から、 $\theta=\omega t$ と示すことができます。
よって、コイルの磁束に対する断面積 $S’$ は、 $S’=S \cos \theta=S \cos \omega t$ となります。
(1) より、 $\Phi=BS’=BS \cos \omega t$
ここでファラデー電磁誘導の法則 $V=-\dfrac{\mathrm{d}\Phi}{\mathrm{d}t}$ より、
$V=-\dfrac{\mathrm{d}\Phi}{\mathrm{d}t}$
$~~~=-\dfrac{\mathrm{d}}{\mathrm{d}t}\left(BS \cos \omega t \right)$
$~~~=BS\omega \sin\omega t$
ここで、$\sin\omega t$ の最大値は1であるから、$V$ の最大値は $BS\omega$ です。
よって、最大の $V$ を $V_0$ としてやれば、 $V_0=BS\omega$ となります。
つまり交流は、 $V=V_0\sin \omega t$ と書くことができ、これは、交流の電圧が $-V_0 ~ V_0$ の間で周期的に($\sin$ 関数として)変化することを示しています。
ここで $\omega$ は回転運動における角速度ですが、ここでは角周波数(角振動数)と呼びます。
この $\omega$ は回転運動と同じことなので、 $\omega = \dfrac{2\pi}{T}=2\pi f$ となります。
( $f$ : 交流周波数 単位 Hz 、 $T$ : 周期 単位 s また、 $f=\dfrac{1}{T}$ )
$f$ は東日本で 50 Hz 西日本で 60 Hz です。
まとめ
交流電源 $V=V_0\sin \omega t$ ちなみに $\cos$ でも同じことです。
角振動数 $\omega$ $\omega=\dfrac{2\pi}{T}=2\pi f$
交流の基礎2 交流と抵抗





































コメント