交流と抵抗 交流の基礎 2
電磁気の記事は次を参照してください。

ここでは交流と抵抗の関係について考えていきます。
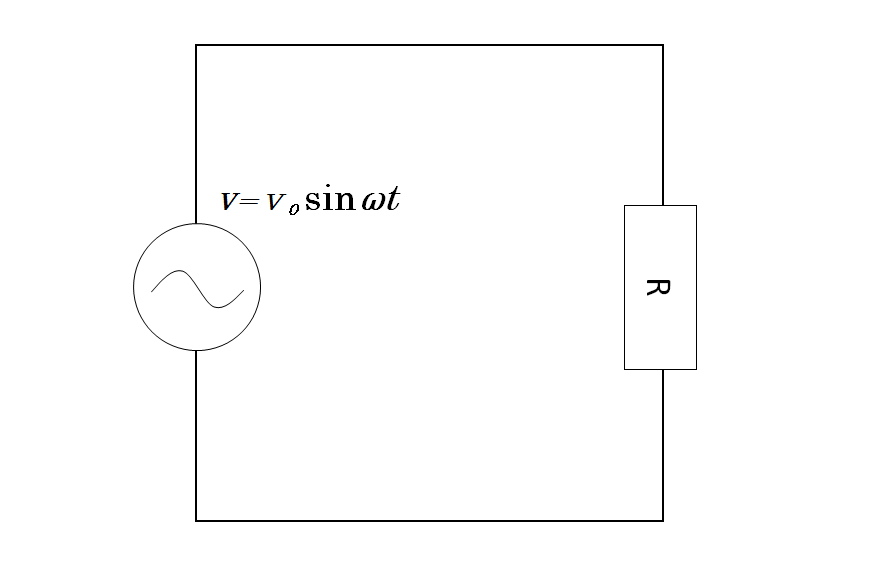
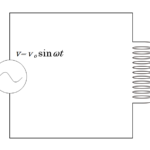
交流電源と抵抗 $R$ をつないだだけの回路を考えましょう。
電源は $V=V_0\sin \omega t$ で変化するものとします。
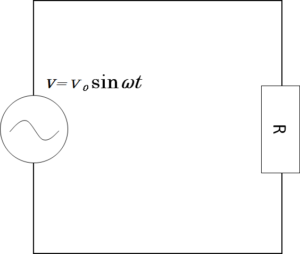
キルヒホッフの法則より $V=RI$
よって、 $V=V_0\sin \omega t$ を代入して、
$I=\dfrac{V}{R}$
$~~~=\dfrac{(V_0 \sin \omega t)}{R}$
$~~~=\dfrac{V_0}{R}\sin \omega t$
ここで、 電流の最大値 $I_0=\dfrac{V_0}{R}\:\cdots\cdots\:(\ast)$ とすると、
$I=I_0 \sin \omega t$
この場合、抵抗を流れる電流と電圧の間には、コイルやコンデンサーで見られるような位相のずれはありません。
抵抗における消費電力 $P$ を考えます。
$P=IV$ であるから、 $I=I_0 \sin \omega t$ と $V=V_0\sin \omega t$ より、
$P=IV$
$~~~=(I_0 \sin \omega t)(V_0\sin \omega t)$
$~~~=I_0V_0 \sin ^2 \omega t$
$~~~=I_0V_0\dfrac{1-\cos 2\omega t}{2}$

$\cos (\alpha+\beta)=\cos \alpha \cos \beta – \sin \alpha \sin \beta $
$\beta=\alpha$
$\cos (2\alpha)=\cos ^2\alpha – \sin ^2\alpha $
$~~~~~~~~~=(1-\sin ^2\alpha )-\sin ^2\alpha $
$\sin ^2\alpha = \dfrac{1-\cos 2\alpha }{2}$
$\cos$ の値の時間平均は 0 であると考えられるため、

なぜって、これ足したら 0 ですよね。

平均の消費電力 $\overline{P}$ は、
$\overline{P}=I_0V_0\dfrac{1-\cos 2\omega t}{2} \: \cdots $ $\cos 2\omega t \: \rightarrow \: 0 $ として
$~~~=\dfrac{1}{2}I_0V_0$
これを次のように変形します。
$\overline{P}=\dfrac{1}{\sqrt{2}}I_0 \times \dfrac{1}{\sqrt{2}}V_0$
ここで
$I_e=\dfrac{1}{\sqrt{2}}I_0$ $V_e=\dfrac{1}{\sqrt{2}}V_0$
とし、これら $I_e$、$V_e$ を実効値と呼びます。
したがって、交流の消費電力は直流の場合と同様に、次のように表せます。
$\overline{P}=I_eV_e$
また、$(\ast)$ より、実効値、最大値ともに
$V_0=RI_0$ $V_e=RI_e$ が成り立っています。
まとめ
- 電流と電圧の最大値 $I_0$ $V_0$
- 実効値 $I_e$ $V_e$
$I_e=\dfrac{1}{\sqrt{2}}I_0$
$V_e=\dfrac{1}{\sqrt{2}}V_0$
- 消費電力
実効値を使えば交流の消費電力 $\overline{P}$ は$\overline{P}=I_eV_e$
と示せます。
- オームの法則
$V_0=RI_0$ $V_e=RI_e$
次回
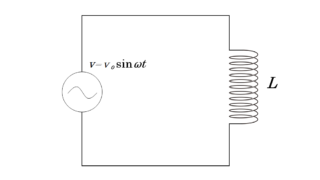
交流の基礎3 交流とコイル



















コメント