サイクロトロン
サイクロトロンとは、荷電粒子を加速するための装置の一つです。
サイクロトロンはローレンツ力と電場からの力の組み合わせにより、荷電粒子を加速することができます。
サイクロトロンは円運動しながら加速していくため、直線加速器にくらべて、非常にコンパクトにできるのが特長です。
ローレンツ力
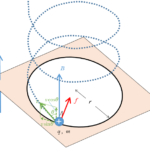
磁場中にある荷電粒子は磁場から、荷電粒子の運動に対して垂直な方向に力を受けます。
これが、ローレンツ力です。
このとき、ローレンツ力が向心力となり、荷電粒子は円運動をします。
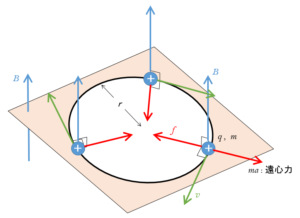
磁場に対して荷電粒子を入射すると、荷電粒子はローレンツ力を受けて運動方向を変えますが、ローレンツ力は荷電粒子に対して仕事をしないため、磁場によるローレンツ力だけでは全体のエネルギーは増えも減りもしません。
ここまでのお話は以下の記事にて解説しています。
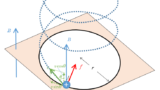
この際、重要なことをもう一度おさらいしておきましょう。
- 磁場が一様な場合、荷電粒子は等速円運動する
- 粒子が同じで磁場が一定であれば、回転周期 $T$ は、荷電粒子の速さや回転半径に無関係に一定である
ここで、2つ目の、回転周期が半径や速さによらない、ということを利用して加速器に応用します。
粒子加速器
さて、荷電粒子を加速する装置を「加速器」と呼びますが、その一つがサイクロトロンです。
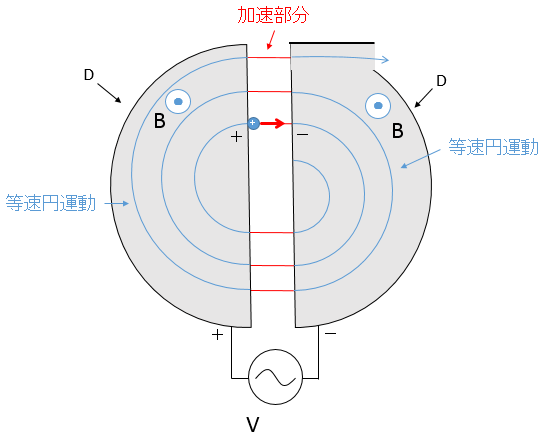
サイクロトロンは、D(ディー)とよばれる電極を二つ対向させたものですが、このDは中が中空になっており、そこを荷電粒子が運動します。
先ほど述べたように、ローレンツ力は荷電粒子に仕事をしないため、その運動エネルギーを増加させて粒子を加速させることはローレンツ力だけではできません。
ここで、加速させるための仕掛けは、電場からの力です。
電場の大きさが $E$ であるとき、電荷 $q$ の粒子は電場から、 $F=qE$ の力を受けます。
Dを交流電源に接続してやれば、左右のDの $+-$ は、一定時間で入れ替わることができます。
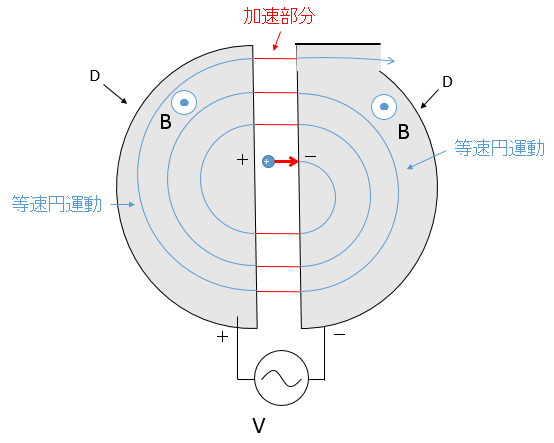
そこで、次の図のような仕掛けを考えます。なかなか巧妙ですね。
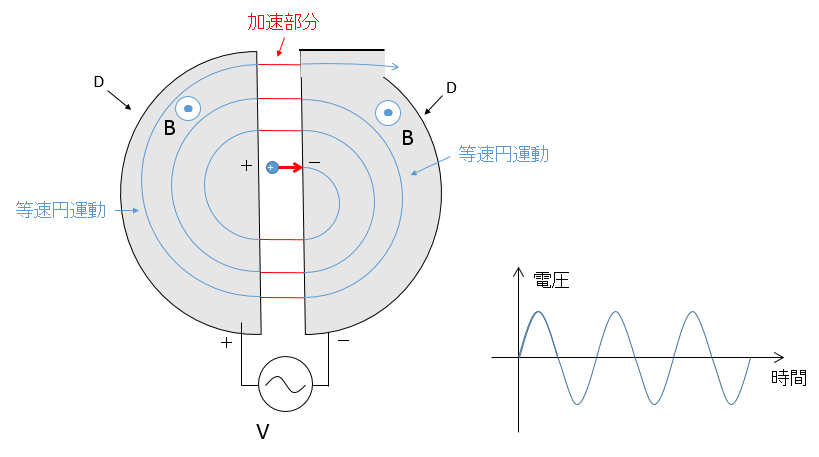
まず、装置の中心付近で荷電粒子(ここでは+)を放出します。
2種類のDは交流電源に接続されていて、今、図の右側は $-$ に、図の左側のDは $+$ に帯電しています。
この場合、2種類のDの間には電場が生じます。
このD間の電場により、荷電粒子がこのギャップにあるときに加速されます。
(図ではわかりやすくするためギャップを大きく描いています。)
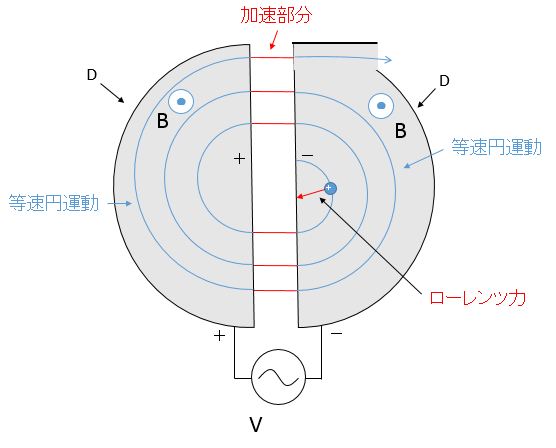
ついで、右側のDで、荷電粒子はローレンツ力を受けて、Dの中を等速円運動するのですが、その周期 $T$ は粒子の速さ $v$ によらず一定です。
つまり、Dの中を半周する時間は、粒子の速さに関わらずいつも同じです。
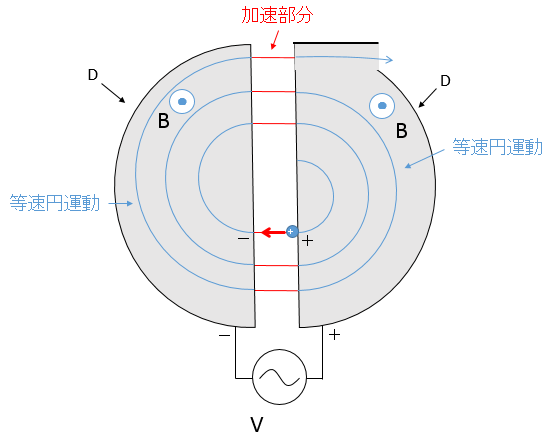
時間 $\frac{T}{2}$ だけ等速円運動すると、またギャップに出ます。
このタイミングで交流により、今度は左のDが $-$ に帯電し、右のDが $+$ に帯電することになります。
そのため、荷電粒子は、再びギャップで加速されることになります。
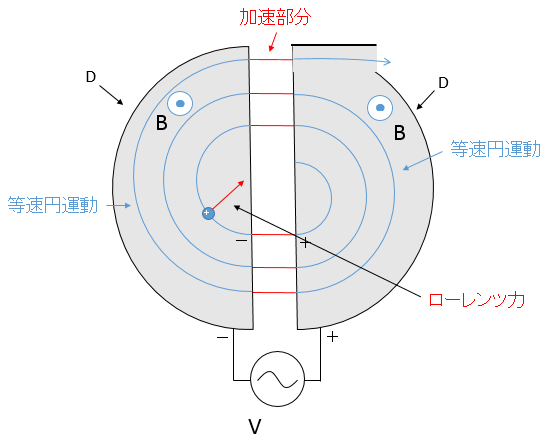
次に、左側のDで等速円運動し、半周します。この場合ももちろん周期は同じままです。
これらを繰り返すことにより、ギャップを過ぎるごとに、少しづつ加速されていく、というわけです。
そして、十分な速さになったら取り出します。




































コメント