ローレンツ力を受ける荷電粒子の運動

ローレンツ力を受ける荷電粒子の運動

一様な磁場 $B$ の中に、荷電粒子がある速度をもって進入した場合の運動について考えます。

結論から言えば次のことが言えます。

• ローレンツ力は荷電粒子に対して仕事をしない　よってエネルギーは増減しない
• 磁場に垂直に進入した場合は、荷電粒子は等速円運動をし、その周期は荷電粒子の速さに無関係である
• 磁場に斜めに進入した場合は、螺旋運動をおこなう

それでは、それぞれについて詳しく考えていきましょう。

ローレンツ力は荷電粒子に対して仕事をしない

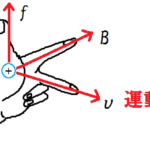
ローレンツ力で解説したように、荷電粒子の速度とローレンツ力は、お互いに垂直の方向にあります（図）。

この場合、 仕事＝力 × 距離　であることから、ローレンツ力は荷電粒子に対して仕事をしません。

よって、運動する荷電粒子にローレンツ力がはたらいても、荷電粒子のエネルギーの増減はありません。

磁場に垂直に進入した場合

次に、具体的な場合について考えていきましょう。

まず、電荷 $q$ ・質量 $m$ の荷電粒子が一様な磁場 $B$ に、速さ $v$ で、磁場に対して垂直に進入した場合です。

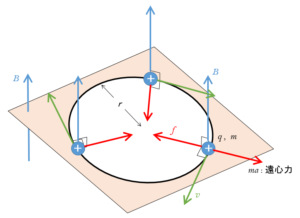
荷電粒子は等速円運動をする

図の場合には、荷電粒子は、その速度の方向と垂直な方向に力を受け円運動します。
磁場が一様なので、等速円運動になります。

その回転半径を $r$ とした場合、 遠心力 = ローレンツ力　（あるいはローレンツ力を向心力とした加速運動） が成り立つので

$ma=f$　　　　ここで、ローレンツ力　$f=qvB$　代入して、

$m\dfrac{v^2}{r}=qvB$　　　より、

$r=\dfrac{mv}{qB}$　　　　が得られます。

周期は荷電粒子の速さに無関係

重要なことの一つに、周期の問題があります。
荷電粒子が円周を1周する周期 $T$ は、

$T=\dfrac{2\pi r}{v}$　　　　より、上で得られた　$r=\dfrac{mv}{qB}$　を代入すると、

$T=\dfrac{2\pi m}{qB}$

となり、磁場大きさ $B$ が一様なら、周期 $T$ は荷電粒子の速さ $v$ に無関係に一定です。

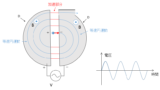
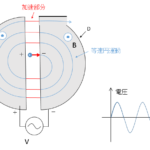
これを利用したのが、サイクロトロンです。
サイクロトロンは、荷電粒子の回転周期が、その速さによらないことを利用して、粒子を加速するものです。

サイクロトロン

荷電粒子を加速するための装置の一つが今回解説する「サイクロトロン」です。 サイクロトロンはローレンツ力と電場からの力の組み合わせにより、荷電粒子を加速することができます。 サイクロトロンは円運動しながら加速していくため、直線加速器にくらべて、非常にコンパクトにできるのが特長です。

kokolainen.com

また、電気量 $q$ を質量 $m$ で割ったもの、$\frac{q}{m}$ を比電荷と呼びます。

比電荷は　$\dfrac{q}{m}=\dfrac{2\pi}{BT}$　となり、

 

$B$ と $T$ を測定すると得られる。

この、比電荷は粒子の種類によるから、

物質の種類を特定するてがかりになる。

磁場に斜めに進入した場合

それでは、磁場に対して斜めに進入した場合はどうなるでしょうか？
この場合は、螺旋運動をすることになります。

螺旋（らせん）運動

ただし、この場合もローレンツ力は荷電粒子に対して仕事はしないので、粒子の運動エネルギーの増減はありません。

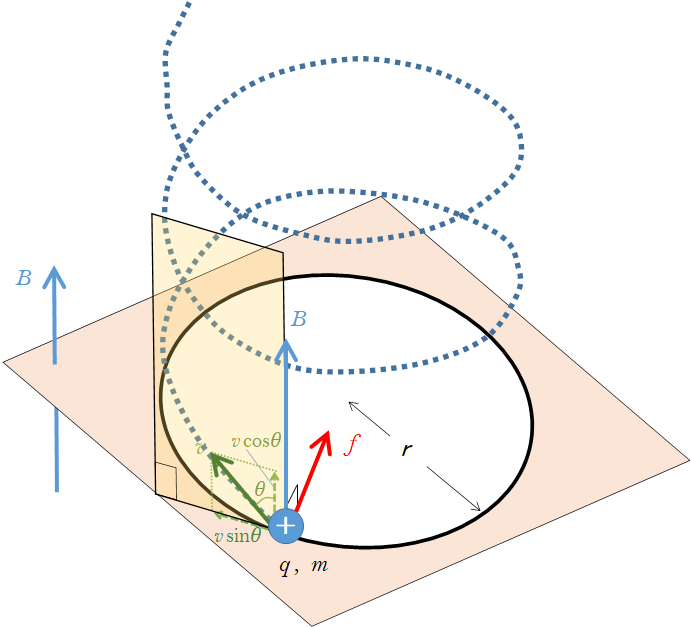
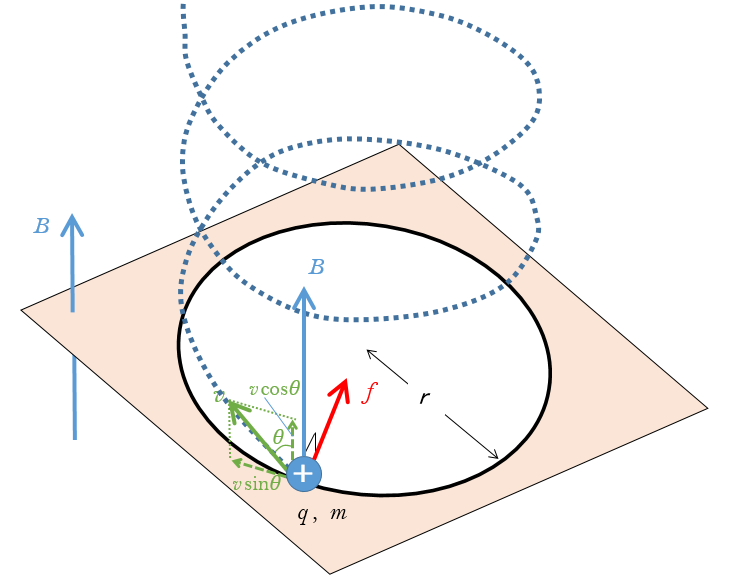
磁場に斜めに速さ $v$ で進入したとします。磁場となす角を $\theta$ とします（図）。
そのとき、磁場に垂直な方向にはローレンツ力を受けることになりますが、磁場と平行な方向には力はかかりません。

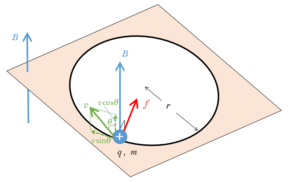
すなわち、図より、$v$ の速さの磁場に平行な成分である、$v\cos \theta$ は、そのままの速さを維持します。

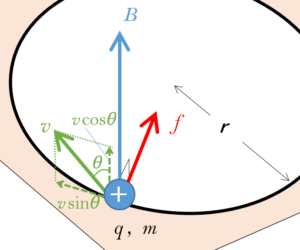
また、磁場に垂直な成分である、$v\sin\theta$ に対してローレンツ力がかかりますから、ローレンツ力の大きさは

$f=q(v\sin\theta)B$　　　　となります。

そのため、磁場に垂直な方向では、回転半径 $r$ が

$r=\dfrac{mv\sin\theta}{qB}$

となるような円運動をするのですが、同時に磁場の方向に $v\cos\theta$ のまま等速運動します。

ということは、等速円運動をしながら磁場の方向に等速運動をするということになりますから、結局は螺旋（らせん）運動をする、ということになります。