エネルギーの原理
エネルギーの原理
質量 $m$ の物体の初速度の大きさ $v_0$、加速度 $a$、変位 $x$、で、速さが $v$ に変化したとすると、
$v^2-v_0^2=2ax$ より、
$a=\dfrac{v^2-v_0^2}{2x}$
として、ニュートンの運動方程式 $ma=F$ へ代入すると、
$m\left(\dfrac{v^2-v_0^2}{2x}\right)=F$
$\dfrac{1}{2}mv^2-\dfrac{1}{2}mv_0^2=Fx$
整理して、
$\dfrac{1}{2}mv_0^2+Fx=\dfrac{1}{2}mv^2$
が得られます。
ここで、$F$ は物体が受けた力であり、 $W=Fx$ において、 $W$ を仕事(=力×変位) とします。
よって、
$\dfrac{1}{2}mv_0^2+W=\dfrac{1}{2}mv^2$
ここで、 $E_0=\dfrac{1}{2}mv_0^2$ $E=\dfrac{1}{2}mv^2$ をそれぞれ、運動エネルギーとします。
そうすると、エネルギーの原理として
$E_0+W=E$
が得られます。
これを言葉で表すと、
最初の運動エネルギー + 仕事 = 最後の運動エネルギー
となります。
教科書や参考書では、引き算の
仕事 = 最後の運動エネルギー ー 最初の運動エネルギー
$W=E-E_0$
となっていることが多いですが、
最初の運動エネルギー + 仕事 = 最後の運動エネルギー
というのが時系列的で、人間の感覚に合っていると思います。
つまり、仕事を受けると運動エネルギーが変化する。というわけですね。
注意
エネルギーの原理とは、ニュートンの運動方程式の変形から、
$\dfrac{1}{2}mv_0^2+Fx=\dfrac{1}{2}mv^2$
最初の運動エネルギー + 仕事 = 最後の運動エネルギー
ということになり、エネルギーは運動エネルギーです。
ここでエネルギーを位置エネルギーにまで拡張して、すなわち力学的エネルギーとして考えてみましょう。
例題
斜面での物体の運動について考えてみます。
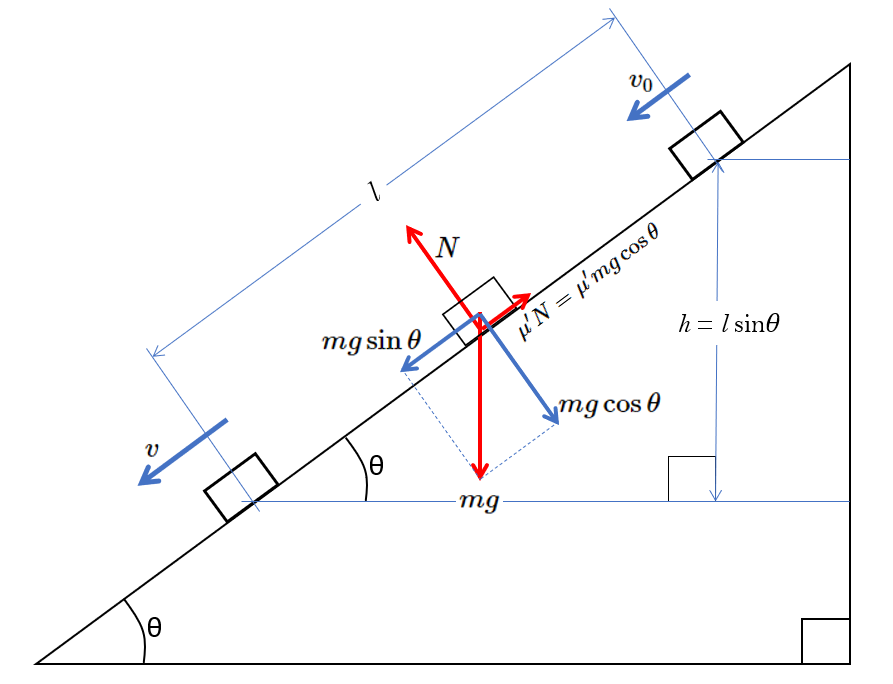
角度 $\theta$ の斜面で、時刻 $t=0$、初速度 $v_0$ で運動を始めた物体が、斜面に沿って $l$ だけ滑り降りた時の速さ $v$ を求めましょう。
図において、質量 $m$ 、重力加速度 $g$ 、斜面と物体の間の運動摩擦係数 $\mu’$ とします。
$N$ は垂直抗力、重力 $mg$ の斜面に平行・垂直な成分はそれぞれ、 $mg\cos \theta$ 、 $mg\sin \theta$ となります。
また、物体にはたらく動摩擦力は $\mu’ N=\mu’ mg\cos\theta$ です。
エネルギー ⇒ 運動エネルギー として考える
初めの運動エネルギー + 仕事 = 最後の運動エネルギー
初めの運動エネルギー +(重力による仕事+摩擦力による仕事)= 最後の運動エネルギー
\begin{eqnarray}
\dfrac{1}{2}mv_0^2+\left\{ mg(l\sin\theta)-\mu’mg\cos\theta \times l) \right\}=\dfrac{1}{2}mv^2\:\cdots(1)\\\\
\end{eqnarray}
この場合の仕事は、保存力による仕事・非保存力による仕事を共に含めます。
エネルギー ⇒ (位置エネルギー + 運動エネルギー) として考える
最下端を重力による位置エネルギーの基準とすると、
(初めの運動エネルギー + 位置エネルギー)+ 摩擦力による仕事 =(最後の運動エネルギー + 位置エネルギー)
より、
\begin{eqnarray}
\left(\dfrac{1}{2}mv_0^2+mg(l\sin\theta)\right)+(-\mu’mg\cos\theta \times l)=\left(\dfrac{1}{2}mv^2+0\right)\:\cdots(2)\\\\
\end{eqnarray}
これらの式 $(1),\:(2)$ は、よく見れば同じです。
この式を解いて $v$ を出せばよいでしょう。
注意点として、この時の仕事は保存力による仕事を入れてはいけません。
それは位置エネルギーとしてすでに組み込まれています。
この場合の仕事は、非保存力による仕事を考えるようにしてください。
勘違い
エネルギーでよくある勘違いが、
(最初の力学的エネルギー)+(重力による仕事+摩擦力による仕事)= (最後の力学的エネルギー)
としてしまうことです。
これをしてしまうと、位置エネルギーを二重にカウントすることになりますので注意が必要です。
エネルギー保存則
保存力以外の外部からの仕事 $W$ が $0$ であるなら、エネルギー保存則として次の式が得られます。
最初のエネルギー = 最後のエネルギー
$E_0=E$
この場合のエネルギーを、 運動エネルギー + 位置エネルギー とすれば、力学的エネルギー保存則となります。
初めの(運動エネルギー + 位置エネルギー)= 後の(運動エネルギー + 位置エネルギー)




































コメント