コンデンサーを含む回路
コンデンサーを含む回路について解説します。
大きく分けて、コンデンサーを含む回路の問題の注意点は３つあります。
- コンデンサーを含む回路に直流電源から電流を流すとき、スイッチを入れた直後はコンデンサーは導線とみなしてよい。
- コンデンサーを含む回路に直流電源を接続し電流を流すとき、十分時間が経過した後は、コンデンサーは断線とみなしてよい。
- コンデンサーのつなぎ変え問題については、電荷総量が保存されることに注意する。
- 交流の場合、コンデンサーは交流を通すように見える。
スイッチを入れた直後はコンデンサーは導線
コンデンサーに最初電荷がない場合、電極に電荷が入るのに、抵抗なくすんなり入り込むことができます。
つまり、電源のスイッチを入れた直後では、コンデンサーは単なる導線とみなしてよいのです。
これはその瞬間・一瞬だけの話です。
しかし、しばらくたつと、コンデンサーの極板には電荷がたまってくるため、さらに電荷を押し込むためには電圧が必要になります。
満員のプラットフォームにからの電車が来た時のことを想像してください。
電車のドアが開くと、最初は人がどっとなだれ込むでしょう。
しかし、混雑してくると押し合いしたり、駅員に押してもらわなければ、車内に入ることができません。
それと同じようなイメージです。
最近ときどき見かける、スーパーキャパシタといわれるものは $5.6\:$F などという大容量です。
このような超大容量のコンデンサーを回路にうかつにつないでしまうと、スイッチを入れて電流を流した後、ほとんどショートしたのと同じように電流が流れることになり、注意が必要です。
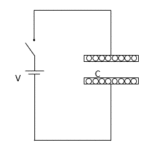
十分時間が経過した後は、コンデンサーは断線
回路に直流電流を流して、十分に時間が経過したとします。
そうすると、コンデンサーはフル充電されたと考えられるので、それ以上電流が流れることはありません。
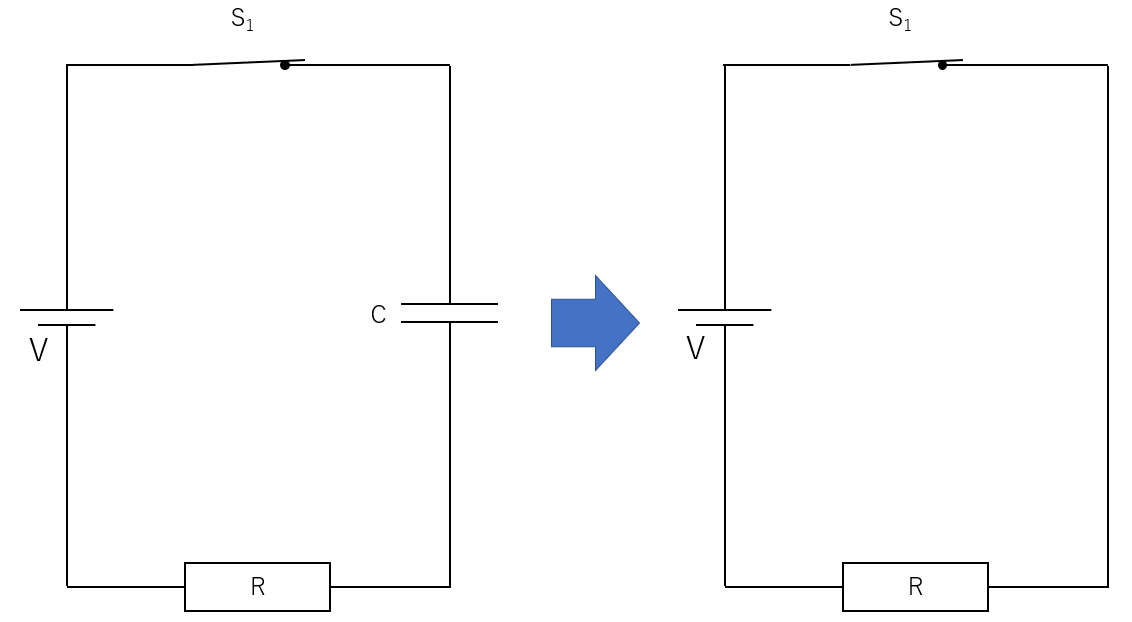
そのとき、例えば次の図のような回路では、十分時間が経過した後は、抵抗があっても電流が $0$ のため、抵抗による電圧降下はありません。
導線・抵抗は電流が流れていないため同電位です。
ですから、コンデンサーの両端電圧と電源の電圧は等しくなります。
上図では、コンデンサーの電圧は電池電圧 $V$ に等しくなります。
たとえて言うなら、
満員になってしまった電車には、もう誰もの乗れず、次の電車を待ちますね。それと同じようなイメージです。
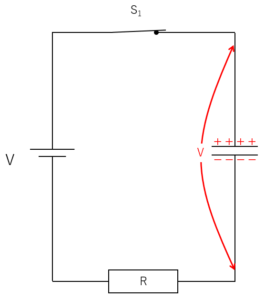
コンデンサーが2つ以上ある時は、各コンデンサーにかかる電圧は、以下の比例式で示されます。
この場合、各コンデンサーに蓄えられる電気量は同じ $Q$ です。
よって、 $V=\dfrac{Q}{C}$ より、
$V_1:V_2=\dfrac{Q}{C_1}:\dfrac{Q}{C_2}=\dfrac{1}{C_1}:\dfrac{1}{C_2}=C_2:C_1$
電荷総量が保存される
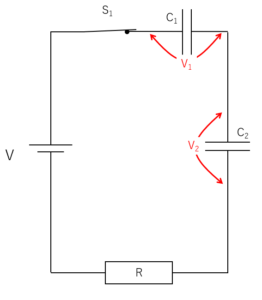
コンデンサーのつなぎ変えの問題などでは、電気的に孤立した部分の電荷総量を考えることがよくあります。
このとき、電気的に孤立しているため、その孤立部分の電荷の総量は保存されます。
これが、電荷保存の法則です。
図の黄色い部分で囲った中の電荷総量は、スイッチをつないでも変わりません。
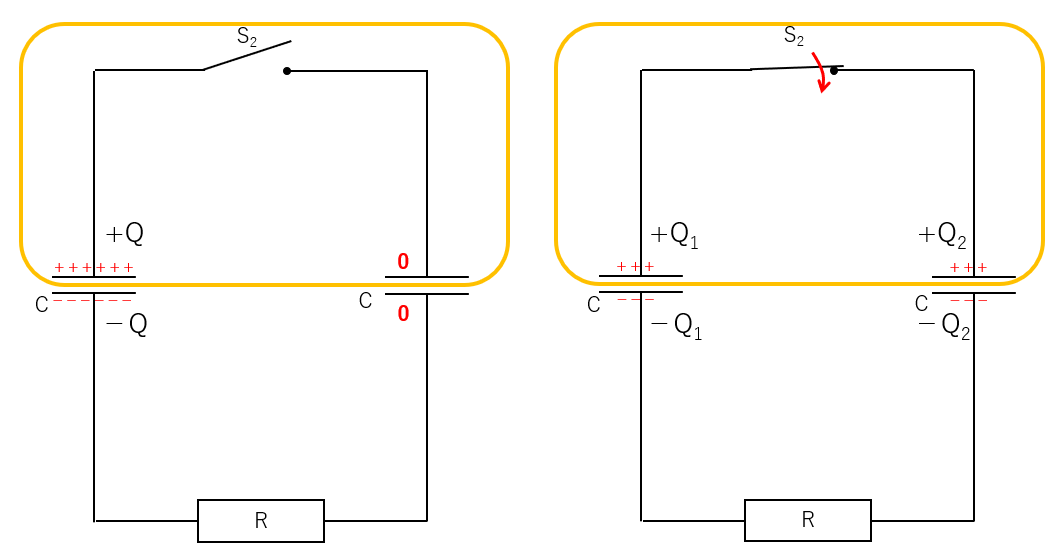
すなわち、
$+Q+0=+Q_1+Q_2$
が成り立ちます。
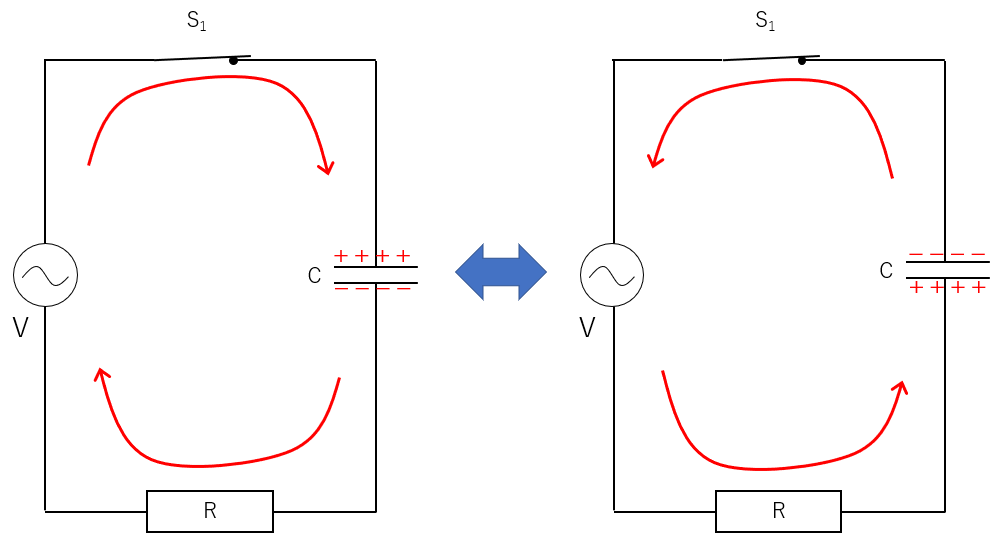
コンデンサーは交流を通す
電流が交流である場合は、コンデンサーは基本的に電流を通すように見えます。
そのわけは、コンデンサーの極板が $+$ に充電されたとすると、次の瞬間には $-$ に充電され、また次の瞬間には $+$ へ・・・と繰り返すからです。したがって、交流の場合は、電流が継続して流れているように見えます。
しかし、実際はコンデンサーに充放電を繰り返しているだけです。
コメント