コンデンサーの充電と電気容量

コンデンサーの充電と電気容量

コンデンサーの充電

電池は、電荷を産み出しません。
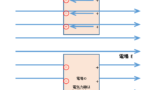
電池は自由電子を運ぶ、電子ポンプの役割をします。

電池電圧が $V$ のとき、電池は $V$ だけ電気的に高いところまで電子を押し上げる働きをします。

コンデンサーと電池を接続すると、電池は＋の極板になる方から電子を引っぺがして、－になる極板まで運びます。

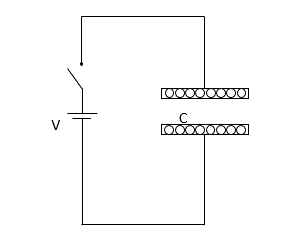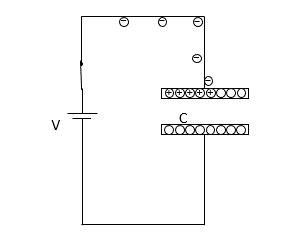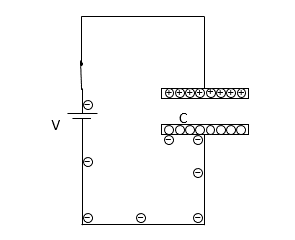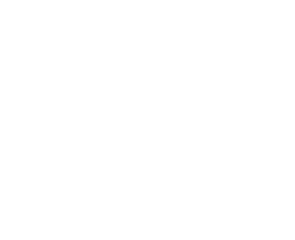
そして、極板間の電圧が電池電圧である $V$ に等しくなるまで充電するのです。
したがって、コンデンサーに蓄えられる電気量 $Q$ は $V$ に比例します。

比例定数を $C$ とすると、コンデンサーに蓄えられる電気量 $Q$ は　$Q=CV$　と示されるはずです。

この $C$ をコンデンサーの電気容量と呼びます。
この比例定数 $C$ はコンデンサーにより違う値をとります。

$C$ は、イメージとしては、バケツの大きさのようなものだと思えばよいでしょう。
$C$ すなわち、バケツの容量が大きいほど電子がたまります。

極板間面積が広いもの、極板間間隔が狭いもの、極板間に誘電体を挟んだものは電気容量 $C$ が大きくなり、電荷がよくたまります。

単位

$Q=CV$ において、$1$V の電圧を加えたとき、$1$C の電荷がたまったとして、

$1=C\times 1$

このときの $C$ は $1$F（ファラド） であるとします。

$1$F（ファラド）は通常使うには大きすぎるので、$1\times {10}^{-6}$F を $1\mu$F（1マイクロファラド）、 $1\times {10}^{-12}$F を $1$pF（1ピコファラド）として用います。 

平行板コンデンサーの電気容量

平行板コンデンサーの電気容量 $C$ について考えてみましょう。

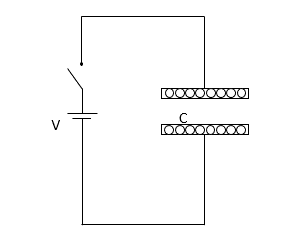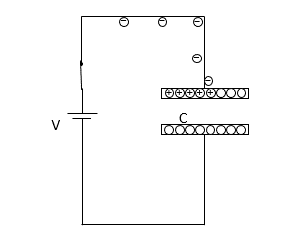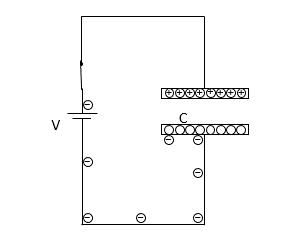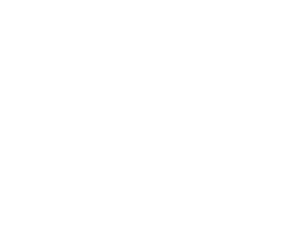
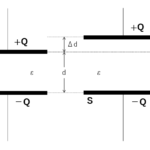
コンデンサーを充電して、電荷 $Q$ が与えられたとします。
そうすると、各極板には $+Q$ 、$-Q$ の電荷がたまっています。

そのとき、ガウスの法則によれば、$Q$ の各電荷からは $4\pi kQ$ 本の電気力線が出ているはずです。
したがって、 $+Q$ 、$-Q$ の両方から合計 $8\pi kQ$ 本の電気力線が出ていることになります。

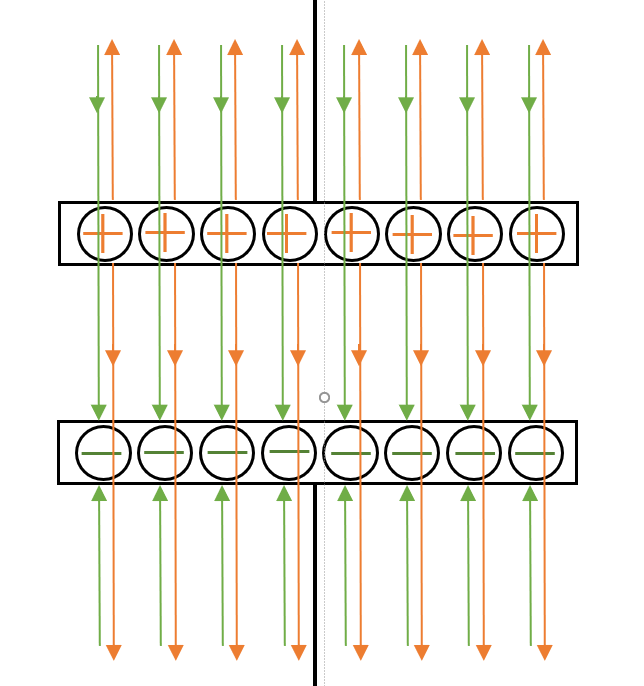
そのうち、コンデンサー外部に出ているものについては、 $+Q$ 、$-Q$ からの電気力線が逆方向を向くため互いに打ち消しあうことになり、コンデンサーの外側の電場は $0$ と考えられます。

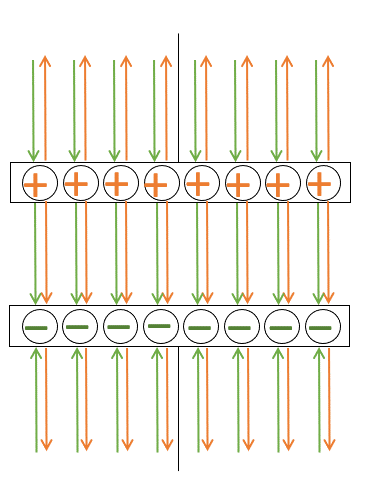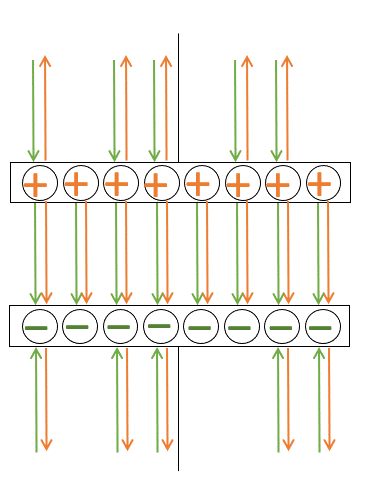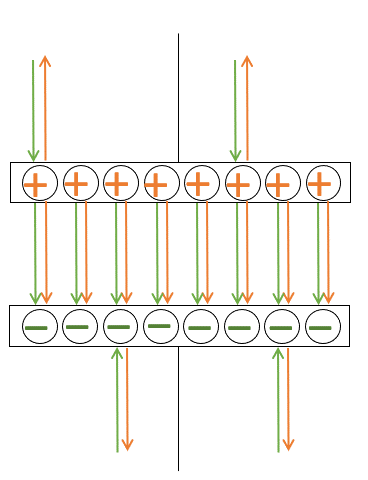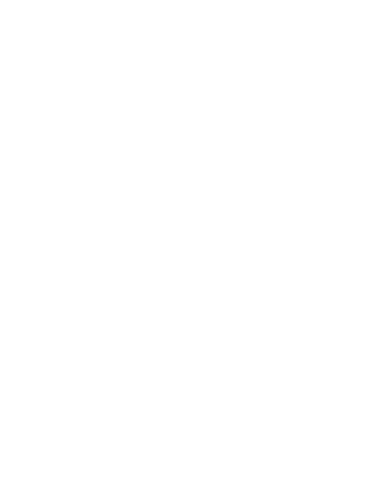
一方、コンデンサー内部は電気力線の方向が一致するため打ち消しあうことはなく、コンデンサーの内部に存在する電気力線は図より、 $8\pi kQ$ 本の半分の $4\pi kQ$ 本です。

ここで電気力線の定義を思い出しましょう。
電場 $E$ では、$E\mathrm{本}/{\mathrm{m}}^2$ の電気力線を引く・・という約束でした。

ここで、コンデンサーの極板面積を $S$ とすれば、その電場 $E$ は次式で与えられます。

$E={\displaystyle \frac{4\pi kQ}{S}}$

次に、コンデンサー内の電場が一様であるとすると、 $E={\displaystyle \frac{V}{d}}$　でしたから、

$E={\displaystyle \frac{4\pi kQ}{S}}={\displaystyle \frac{V}{d}}$

となります。

これより、

$Q={\displaystyle \frac{1}{4\pi k}}\cdot {\displaystyle \frac{S}{d}}V$

と書くことができます。
これと、 $Q=CV$　より、

$C={\displaystyle \frac{1}{4\pi k}}\cdot {\displaystyle \frac{S}{d}}$

ここで、 ${\displaystyle \frac{1}{4\pi k}}=\epsilon$　とおくと、

$C=\epsilon {\displaystyle \frac{S}{d}}$

と書くことができます。この $\epsilon$ を誘電率と呼びます。

特に、コンデンサー内部が真空の場合を真空の誘電率とよび、${\epsilon }_0$ とします。

コンデンサー内に誘電体を入れると

コンデンサー内に誘電体（絶縁体）を挿入すると、一般に誘電分極によりコンデンサーの電気容量が増加します。

関連記事はこちら

導体内・不導体内の電場と電位、グラフ解説

導体内部は電場が０です。そして電気力線は入り込むことができません。 これらのことは知っているとは思いますが、なぜだかはわかっているでしょうか？ ここでは、くどいようですが詳しく説明するつもりです。

kokolainen.com

そのとき、その増加の程度を示すものとして比誘電率 ${\epsilon }_r$ という物理量を導入します。

比誘電率は、その誘電体の誘電率 $\epsilon$ が真空の誘電率の ${\epsilon }_0$ の何倍であるかを示す量です。

したがって、 $\epsilon ={\epsilon }_r{\epsilon }_0$　となります。
これをつかってコンデンサーの電気容量の式は

$C=\epsilon {\displaystyle \frac{S}{d}}={\epsilon }_r{\epsilon }_0{\displaystyle \frac{S}{d}}$

と書くことができます。

例えば、次の表を見ていただくとわかるように、チタン酸バリウムをコンデンサー間に挿入すると、真空の場合に比べ、電気容量が約5000倍にもなります。