みなさん、電場とは何でしょうか?
電場を表す式は、$ E=k\dfrac{Q}{r^2} $ と書けることは学習されたと思います。
しかし、電場とは何か?を自分の言葉で説明することはなかなか難しいのではないでしょうか。
この記事では、この式の意味するところと、電場という場の考え方にたとえ話を入れながら、やさしく説明いたします。
この記事を読めば、いままであやふやだった電場の理解が一層進むはずです。
動画で解説
電場とは
電場とは何でしょうか?と、問われて
・・・$E=k\dfrac{Q}{r^2} $ で示される量です。とか、$E=\dfrac{V}{d}$ です、などという答えが返ってきそうですが、ここではそのイメージから考えていきましょう。
ではまずは、クーロン力のおさらいからです。
クーロン力
クーロン力(電気力)に関するクーロンの法則は次のように表現されます。
電荷 $q$ と$Q$ が距離 $r$ だけ離れているとき、互いに
$f=k\dfrac{qQ}{r^2}$
の力を及ぼしあう。$k \: : $ 比例定数
$q$ と$Q$ が同種の電気を帯びている場合は反発し、異種の場合は引き合う。
このとき、空間を隔てて力が及ぼしあうのですが、なぜ遠く離れたものが力を及ぼしあうのでしょうか?
他には、重力や磁力も同じようなことが言えます。
これらの力は離れたものどうしが力を及ぼしあっていますね。
一方、お互いに触れあって押したり引いたりして力を及ぼしあうのは直感的に理解しやすい現象です。
しかし、このクーロン力などのようにお互い空間をへだてているのにも関わらず力を及ぼしあう現象は、考えてみれば不思議なものです。
遠隔作用と近接作用
ニュートンの時代に万有引力が発見されましたが、なぜ遠く離れた物体間に力が働くのだろうか・・・と考えた時、どうにもその説明がしっくりくるものがありませんでした。
そこで、そういうものとして認めることにしたのです。
つまり、重力や磁力、電気力は空間を超えて伝わることができる・・・というものです。
これを遠隔作用といいます。
ニュートン流の遠隔作用では何もない空間を通して力が作用します。
しかも、ニュートンの「作用反作用」の法則に従えば、遠隔作用ではそれらの力は全く同等に瞬間的に働きあわねばなりません。
しかし、そうは考えなかった男が一人いました。
それが苦学の天才科学者マイケル・ファラデーです。
ファラデーは本屋で働きながら独学で科学を学び、当時の有名な科学者デービーに弟子入りしました。
のちに実験物理や化学で頭角を現していきます。後世、師匠であるデービーの最大の功績は「ファラデーを発見し、世に出したこと」だともいわれています。
ファラデーはこの遠く離れたものどうしが力が及ぼしあう現象を説明するため、場という概念を導入します。
ファラデーが考えた場とはどのようなものでしょうか?
ファラデーは、「空間に電荷がある場合、その周囲の空間が電気的に変形する」、として、その周りの空間を場としたのです。
そして、その場がゆがむことにより力が伝播するというわけです。
これを近接作用といいます。
ちょっと、わかったようでわからない説明ですね。
電場をたとえてみると
電気的に空間が変形する・・・と言われても・・・・。なにそれ?という感じです。
空間ではイメージがしにくいので、次のようなたとえで次元を一つ落として考えてみましょう。
サラダボウルなどにラップをぴったりと張ります。
このラップ表面が空間だとイメージしてください。
さてそのラップの上にボールを載せます。
するとボールの重さを受けて、ラップは下のほうにゆがむでしょう。
つまりラップに載せたボールによって空間がゆがんだ、というわけです。
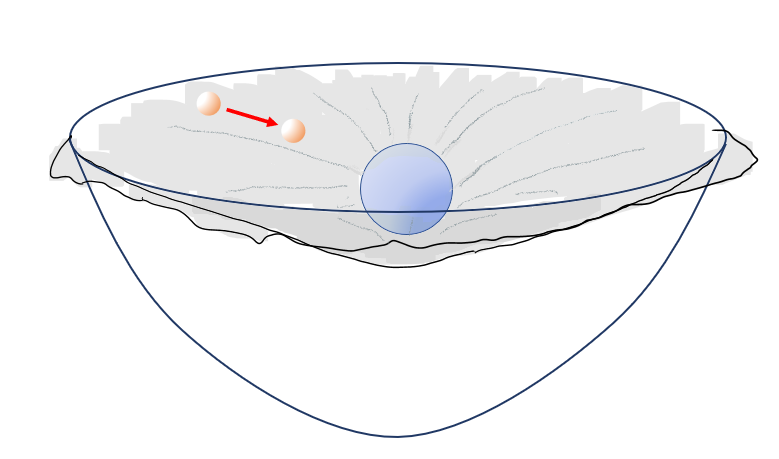
さて、そのままにしてラップにビー玉などをそっと置いてみましょう。
ビー玉はボールに向かって転がっていくでしょう。
ラップがもし目に見えなければ、何もないところを動いていくように感じるはずです。
今度はボールをラップの下から上に突き上げてみましょう。
そうすると今度はラップは凸のように変形しますね。
同じようにラップの一か所にそっとビー玉を置いてやると今度は外に向けて転がっていくはずです。
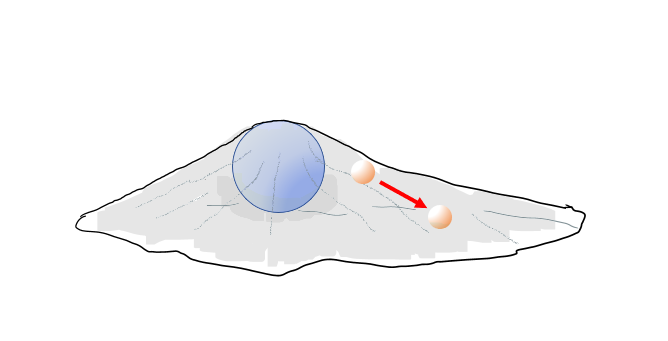
このように、たとえビー玉がなくても、ボールがあるだけでラップが変形しています。
ビー玉が動いたのは大きなボールから直接的な力を受けたのではなく、変形したラップによるものというわけです。
この時のこのラップが場のイメージなのです。
もし、ラップが透明で見えなければ、ラップ(空間)が変形していることはわかりません。
同じようなイメージで、電荷を置いた空間も目には見えないけれど電気的に変形していると考えてみます。
つまり、空間が電気的に変形したために場がゆがみ、その歪みに沿って他の荷電粒子が力を受ける・・・というわけです。
試しに、サラダボウルに置いた物体(電荷)を揺らしてみます。
そうすると、その揺れは空間を伝わり、その速さは有限です。
空間を伝わる電磁波の速さは有限ですね。
このように、空間を変形が伝わるには時間がかかることが直感的に理解できます。
電場を数式で考える
しかし、クーロンの法則は
$f=k\dfrac{qQ}{r^2}$
です。
今、空間に $Q$ の荷電粒子が存在し、周りの空間を変形させていたとします。
このとき、ビー玉に相当する $q$ の電荷をもつ物体が存在しなければ、$f=k\dfrac{qQ}{r^2}$ において $q=0$ で $f=0$ となり、数式的には場を示すことができていません。
このままでは、場の考え方をきちんと表しているとは言えないですね。
そこで、次のような天才的な式変形が考えられたのです。
クーロンの法則ふたたび
おなじみのクーロンの法則を次のように変形します。
$\begin{split}f=&k\dfrac{qQ}{r^2} \\\\
=& q \times k\dfrac{Q}{r^2} \end{split}$
さて、ここで $ E=k\dfrac{Q}{r^2}$ として、この $E$ を場を表す物理量として定義します。
そうすると、$f=qE$ です。
こうすれば、$Q$ という電荷が存在した場合、$q$ が 0 であったとしても
$E =k\dfrac{Q}{r^2}$
である以上、$E \neq 0$ であり、電荷 $Q$ によるある値を持ちます。
そのうえで、働く力はちゃんと $f=0$ となっていますね。
このとき、 この $E$ が電荷$Q$ による場の変形具合を示す量であると考えるのです。
つまり電荷 $Q$ が存在するとき、周りの空間は電気的に変形し、その変形度合いを $E$ でしめす・・・というわけです。
これでファラデーの考えた場を数式でも扱うことができるようになりました。
あなたにも見えないはずの電場の変形がイメージとして浮かんできたのではないでしょうか?
試験電荷
さて、ここでもう一度電場の式を見直してみましょう。
$E=k\dfrac{Q}{r^2}$
ですが、この式は、クーロンの式の $q$ を 1 としたときと同じです。
つまり $q=1$ を代入して、
$f=E=k\dfrac{1\times Q}{r^2}$
ということは、電場の大きさは $+1\:[c\:]$ の電荷を置いたときにその電荷が受けるクーロン力 $f$ と同じです。
そこで、この $+1\:[c\:]$ を試験電荷と呼び、電場の様子を調べるのに使います。
たとえでいうと、
先ほどの目に見えないラップの変形具合を調べるために試験的にビー玉を置いてみます。
そうすると、ビー玉の転がる方向と転がる勢いからラップの傾きの様子を調べることができますね。
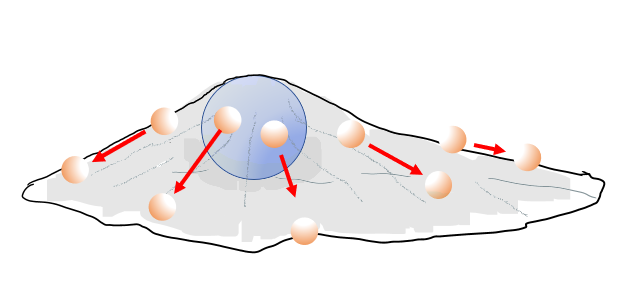
つまり、このビー玉の役割をしているのが試験電荷というわけです。
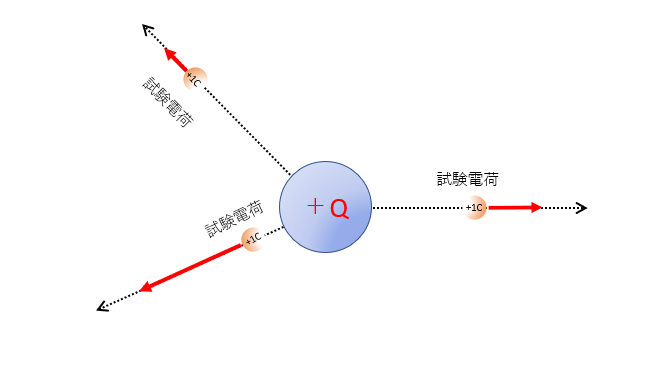
ですから、問題を解くにあたり、その電場の様子を調べたいときには、空間にイメージで試験電荷 $+1\:[c\:]$ をおきます。
そして、その時に受けるクーロン力の方向と大きさを調べることで電場の様子がわかります。
図で示すと
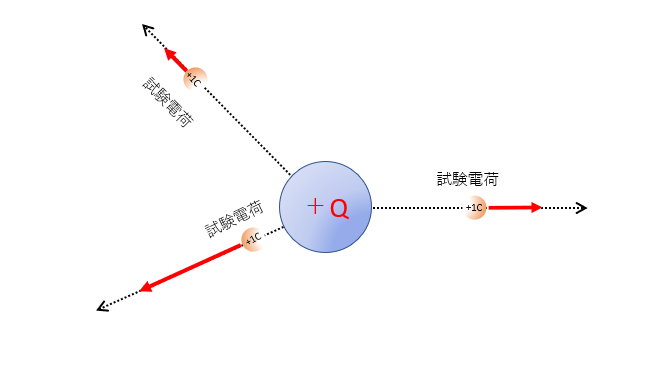
のように、電場の様子を知ることができるのです。
電場まとめ
電荷 $Q$ のまわりに作られる電場は次の式で示される。
$k \: : $ 比例定数、$r$ は電荷からの距離
$E=k\dfrac{Q}{r^2}$
ここで、クーロンの法則
$f=k\dfrac{qQ}{r^2}$
において、$q=1$ とすれば、
$f=E=k\dfrac{1\times Q}{r^2}$
と示せるので、電場の様子は試験電荷 $+1[c\:]$ をおいて調べることができる。
このとき、$+1[c\:]$ の受ける力の大きさが電場の大きさで、力を受ける向きが電場の向きとなる。
電気力線と電場
電気力線と電場について解説しています。





































コメント