コンデンサー極板の及ぼしあう力

コンデンサー極板の及ぼしあう力

コンデンサー内の電場を $E$ とし、極板上の電荷を $Q$ とした場合、コンデンサー極板が受ける力の大きさ $F$ は　$F=\dfrac{1}{2}QE$　で示されます。

よくある問題をやってみましょう。

例題

極板面積 $S$ 、極板間隔 $d$ のコンデンサーに電荷 $Q$ を与えた。誘電率を $\varepsilon$ とする。以下の問いに答えよ。

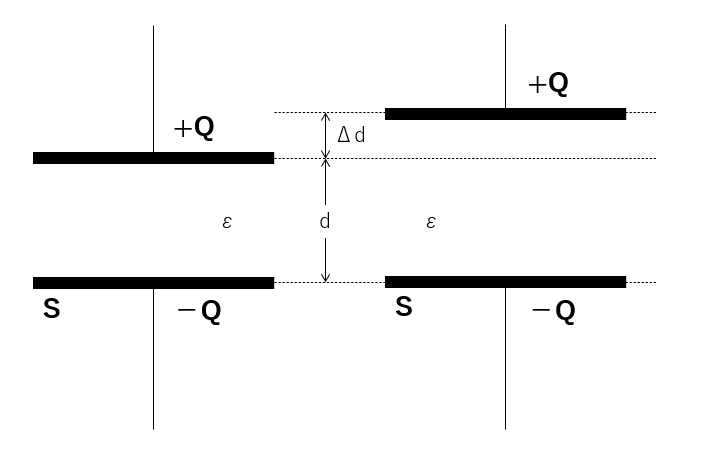
1. コンデンサー内の電場 $E$ を求めよ。
2. コンデンサーの蓄えている静電エネルギー $U$ を求めよ。
3. コンデンサーを電池から切り離した状態で、極板間隔を微小距離 $\Delta d$ だけゆっくりと広げた。
   このときの静電エネルギーの増加量 $\Delta U$ を求めよ。
4. 極板間の及ぼしあう引力 $F$ を求めよ。
5. 4の力 $F$ を $E$ と $Q$ を使って示せ。

答え

1.  コンデンサー内の電場 $E$ を求めよ。

$E=\dfrac{V}{d}$ 　$Q=CV$　$C=\varepsilon\dfrac{S}{d}$　より、

$E=\dfrac{Q}{Cd}=\dfrac{Q}{\left( \varepsilon \frac{S}{d} \right)d} $

$E=\dfrac{Q}{\varepsilon S}$

2.  コンデンサーの蓄えている静電エネルギー $U$ を求めよ。

$C=\varepsilon\dfrac{S}{d}$ と、静電エネルギーの式から
\begin{eqnarray}
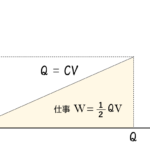
U&=&\dfrac{1}{2}QV\\\\
&=&\dfrac{Q^2}{2C}\\\\
&=&\dfrac{Q^2}{2\left( \varepsilon \frac{S}{d}  \right)}\\\\
&=&\dfrac{dQ^2}{2\varepsilon S}
\end{eqnarray}

3.  コンデンサーを電池から切り離した状態で、極板間隔を微小距離 $\Delta d$ だけゆっくりと広げた。 このときの静電エネルギーの増加量 $\Delta U$ を求めよ。

極板間隔を $\Delta d$ だけ広げた後のエネルギーを $U’$ とすると、2の結果から、

\begin{eqnarray}
U’&=&\dfrac{(d+\Delta d)Q^2}{2\varepsilon S}\\\\
\end{eqnarray}

よって、 $\Delta U=U’-U$　は、

\begin{eqnarray}
\Delta U&=&U’-U\\\\
&=&\dfrac{(d+\Delta d)Q^2}{2\varepsilon S}-\dfrac{dQ^2}{2\varepsilon S}\\\\
&=&\dfrac{\Delta dQ^2}{2\varepsilon S}\\\\
\end{eqnarray}

4.  極板間の及ぼしあう引力 $F$ を求めよ。

エネルギーの原理から

$U+W=U’$

よって　　$W=F\Delta d=U’-U=\Delta U$

\begin{eqnarray}
F\Delta d&=&\Delta U\\\\
&=&\dfrac{\Delta dQ^2}{2\varepsilon S}\\\\
F&=&\dfrac{Q^2}{2\varepsilon S}
\end{eqnarray}

5.  4の力 $F$ を $E$ と $Q$ を使って示せ。

1と4の結果から

$F=\dfrac{Q^2}{2\varepsilon S}$

$E=\dfrac{Q}{\varepsilon S}$

より、

$F=\dfrac{Q^2}{2\varepsilon S}$

$~~=\dfrac {1}{2}QE$

このように、コンデンサー内の電場を $E$ とし、極板上の電荷を $Q$ とした場合、コンデンサー極板が受ける力の大きさ $F$ は　$F=\dfrac{1}{2}QE$　で示されます。

$F=QE$　ではないことに注意しましょう。

なぜ　$F=\dfrac{1}{2}QE$　なのか？

電荷 $q$ が電場 $E$ から受ける力 $F$ の計算は　$F=qE$　です。

コンデンサーの極板はそれぞれ電荷 $Q$ 、$-Q$ を持っています。
コンデンサー内の電場の大きさは $E$ です。

では、コンデンサー極板の受ける力の大きさは　$F=QE$　ではないか？ と多くの人が勘違いします。

なぜ、$\frac{1}{2}$ が付くのでしょうか？

この電荷 $q$ が電場 $E$ から受ける力の式、 $F=qE$　の状況をもう一度思い出してみましょう。

空間に電荷 $Q$ があり、その電荷が作る電場が $E$ であり、その電場に電荷 $q$ を置いたときに、及ぼされる力が　$F=qE$　です。

たとえて言うなら、電荷 $Q$ による電場が次の図の膜である場合、電荷 $q$ は膜上の小球に相当します。このあたりは、 イメージでわかる電場の基礎　を参照してください。

したがって、その電場 $E$ には、その電場に置かれた電荷 $q$ は寄与していません。
感覚的に考えて、電荷 $q$ が作る電場が影響するようにも思いますが、そうではないことに注意しましょう。

したがって、コンデンサーの片側の極板が受ける力は、相手の極板による電場から受ける力のみです。

コンデンサー内の電場が $E$ で示されるとき、片側の極板にある電荷が作るコンデンサー内の電場は $\frac{1}{2}E$ です。

つまり、それらが二つあるから、コンデンサー内の電場は　$\frac{1}{2}E+\frac{1}{2}E=E$　となると考えられます。

そのため、コンデンサーの片側の極板が受ける力は　$F=qE$　より、$F=Q\times \left(\dfrac{1}{2}E\right)=\dfrac{1}{2}QE$　となるのです。