単振動を苦手とする人は多いようです。
また、教科書ではわりとサラリと済ませているので、入試問題になると手が出なくなる人も多く見かけます。
確かに入試では割と難しい問題が出るように思いませんか?
単振動については、問題集でやり込む必要があります。
単振動の式を導く
等速円運動は重要です
単振動を理解するにあたって、等速円運動は非常に重要です。
ここがわかっていないと結局単振動もわかりません。
もし怪しいと思ったらぜひもう一度復習してください。
等速円運動している物体に横から光を当てて壁に影を作りましょう。
数学で言うところの射影ですね。
この影の動きが単振動の動きそのものになります。
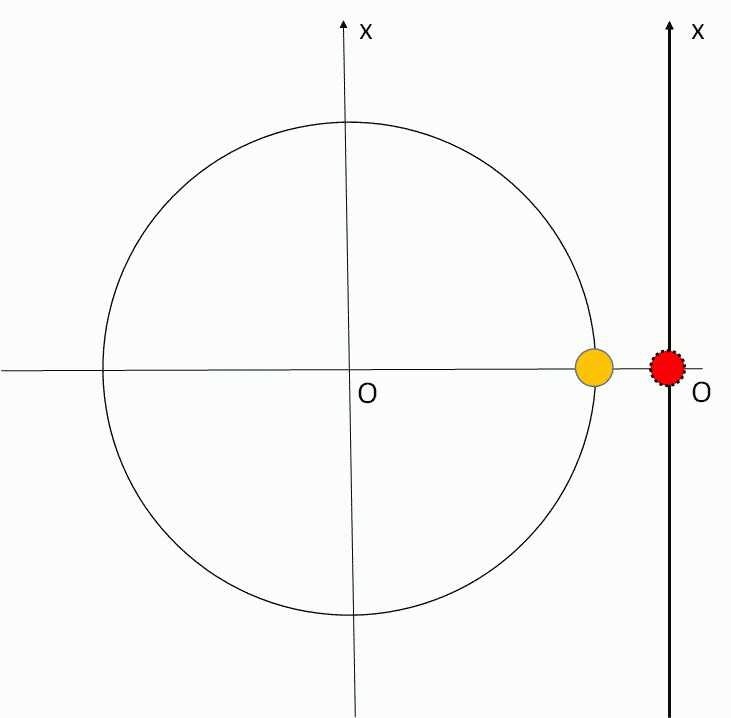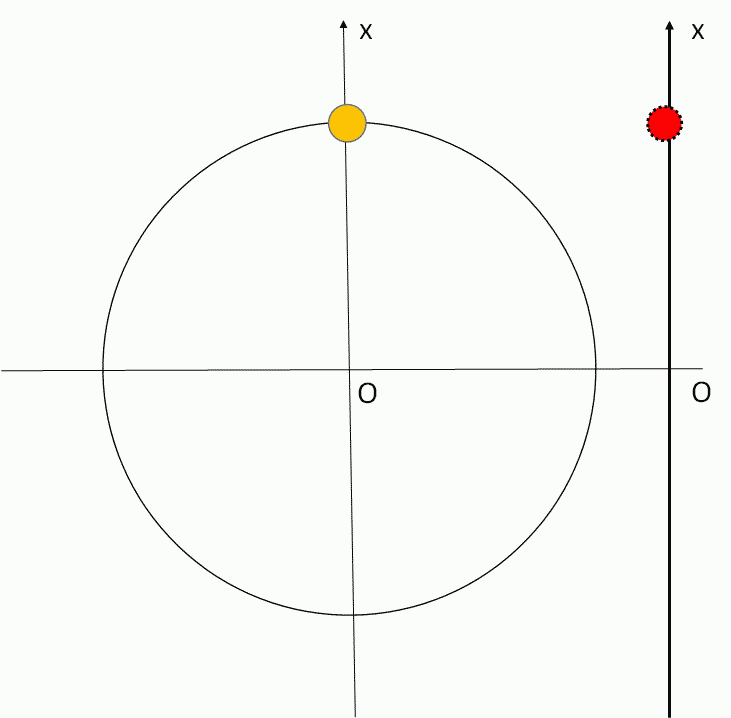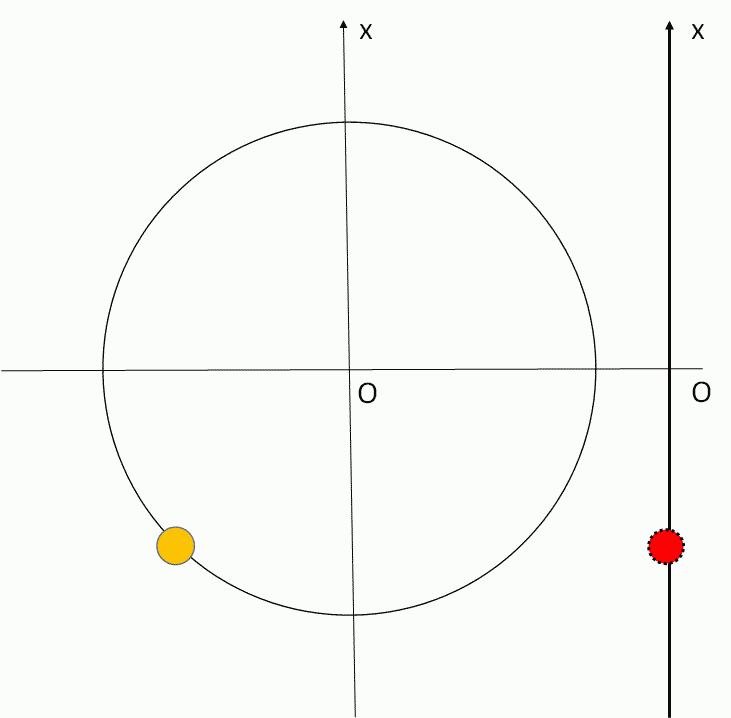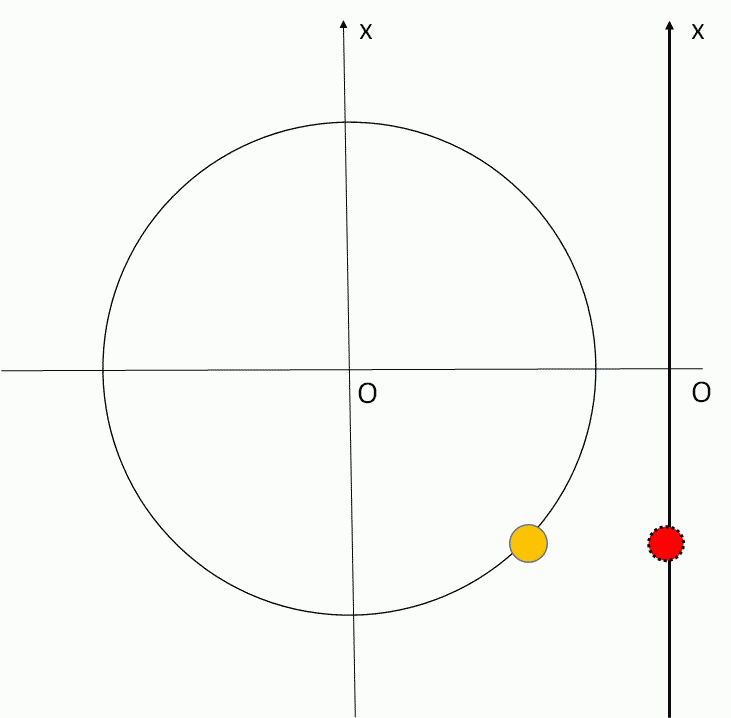
まず重要なことは角速度 $\omega$ です。
$t$ 秒間で角度 $\theta$ 回転したとき角速度 $\omega$ は、
$$\omega=\dfrac{\theta}{t}$$
で示されます。つまり $\theta=\omega \times t$ ですね。
単振動変位 $x$ について考える
それでは変位 $x$ 、速度 $v$ 、加速度 $a$ について考えてみましょう。
ここでは等速円運動の回転半径を A とします。
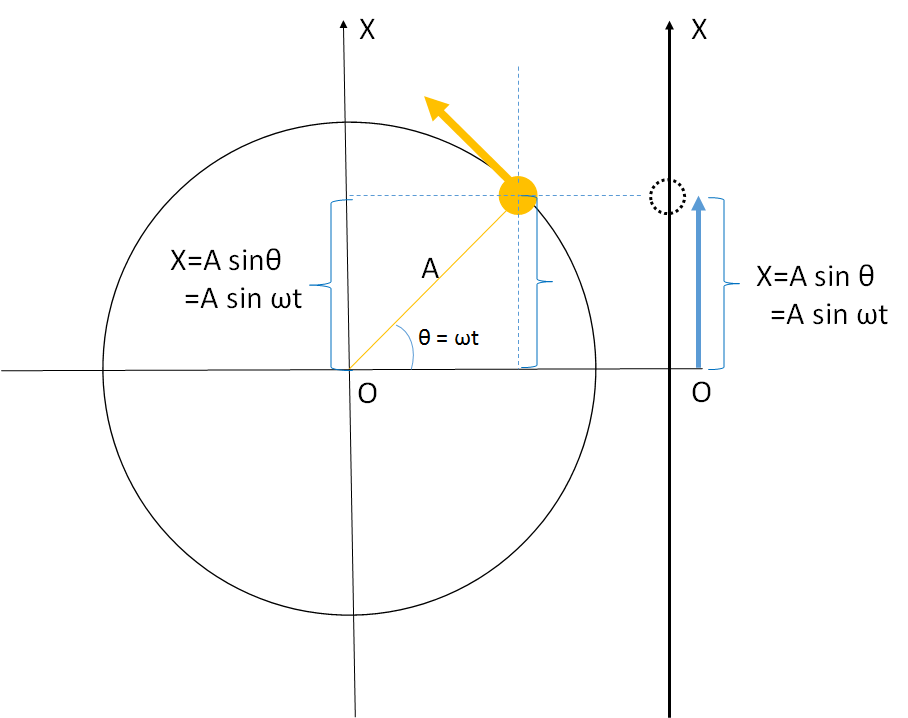
そうすると、
$$x=A\sin\omega t$$
となりますね。
単振動の速度 $v$ について考える
次に速度の式を考えます。
等速円運動ですからその回転の速さを $V$ とします。
ここで、 $V=A\omega$ です。($v=r\omega$ より)
その時の、回転の速さは $x-y$ 方向に分解して考えると図のようになります。
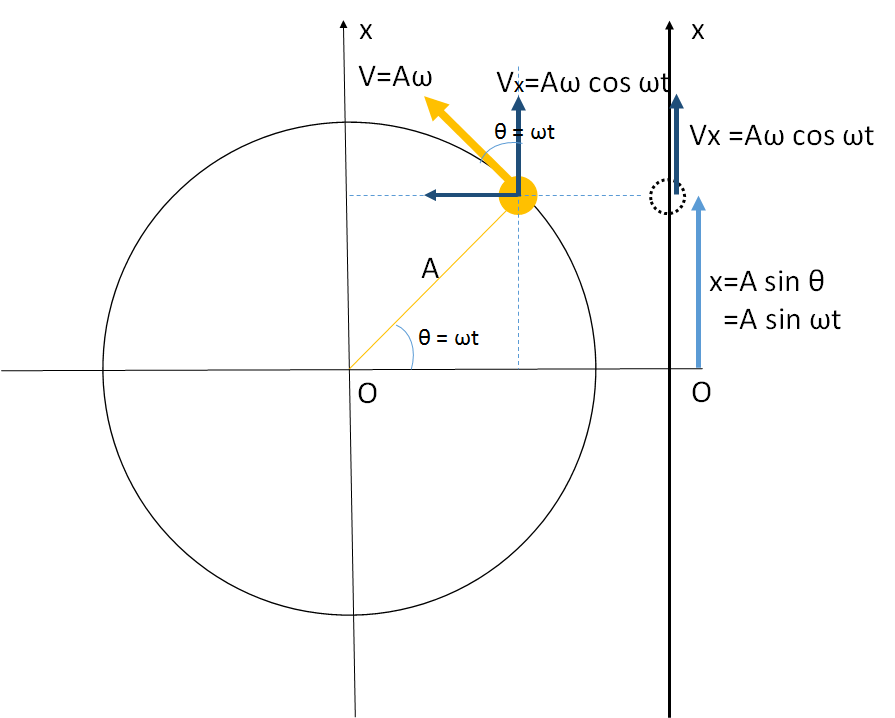
したがって、射影の $x$ 成分が単振動の速度ですから、単振動の速度を $v$ 、等速円運動の $x$ 成分を $V_x$ として、
$$v = V_x = A\omega \cos \omega t $$
となります。
単振動の加速度 $a$ について
続いて同様に単振動の加速度 $a$ も求めてみましょう。
次の図においてやはり等速円運動の加速度の$x$ 成分がわかれば良いので、
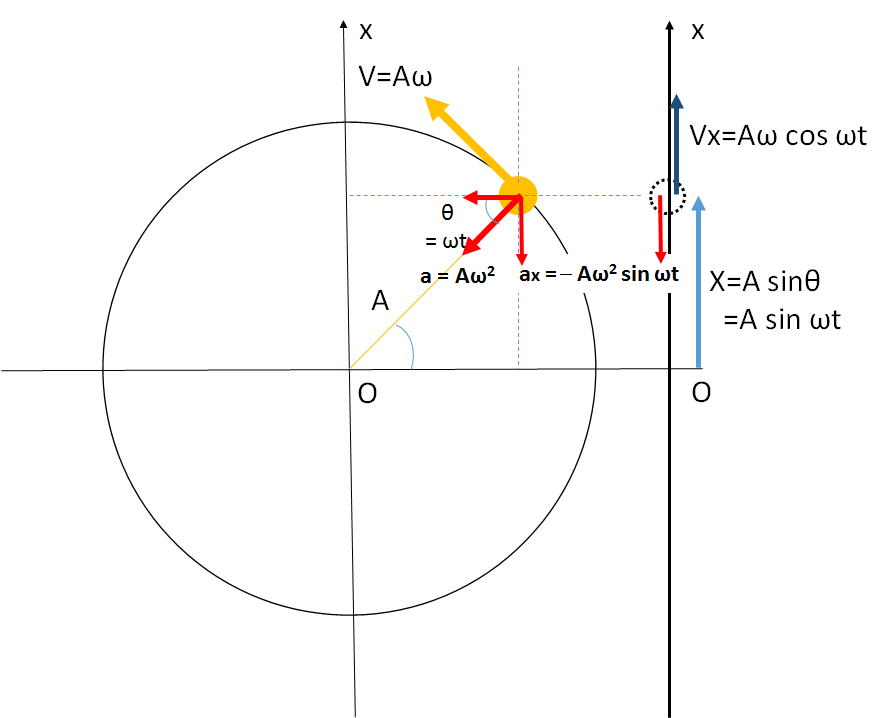
単振動の加速度は
$$a=-A\omega^2\sin \omega t $$
となります。ここでマイナスが付くことに注意してください。
これに $x=A\sin \omega\ t$ を代入することで次の式を得ます。
$$a= -\omega^2 x $$
単振動の力
そうすると運動方程式を適用することで次の式を得ます。
\begin{eqnarray} F & = & ma \\ & = & m(-\omega^2 x) \end{eqnarray}
この式で注意すべきは、変位である $x$ に対して、$a$ も $F$ も常に逆方向であるという点です。 このとき $F$ を復元力と呼びます。
ここで、 $m\omega^2 = k$ とおくことによって、
$$F=-kx$$
となりますから、これはフックの法則そのものです。逆にいえば、力 $F$ がこのような式で表される場合はすべて単振動します。
そして、$m\omega^2 = k$ より
$$\omega=\sqrt{\dfrac{k}{m}}$$
となりますね。また、$\omega =\dfrac{2\pi}{T}$ ですから、
$$T=2\pi \sqrt{\dfrac{m}{k}}$$
となります。
さらに、振動数 $f=\dfrac{1}{T}$ です。
$$\omega=2\pi f$$
と書けますから、
$$f=\dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}}$$
となります。
微積分を使って

GDJ / Pixabay
今までのべてきたことは、微積分を使うことで簡単に導くことができます。
三角関数の微分を知らない人は、とりあえず次の式を覚えましょう(機会があればそのうち解説します)。
$$(\sin kx)’ = k\cos kx \:\:\:\:\:\:\:\:\: (\cos kx)’ = -k\sin kx$$
まず、
$$x=A\sin \omega t$$
これを時間微分 $\dfrac{d}{dt}$ します
\begin{eqnarray}v&=&\dfrac{dx}{dt} \\ & = &\dfrac{d}{dt}(A\sin\omega t) \\ &=& A\omega\cos \omega t\end{eqnarray}
微分すると$\omega$ が前に出ることに注意してください!
同様に、加速度 $a$ を求めましょう。
\begin{eqnarray}a&=&\dfrac{dv}{dt} \\ & = &\dfrac{d}{dt}(A\omega\cos\omega t )\\ &=& -A\omega^2\sin\omega t \\&=& -\omega^2 x \end{eqnarray}






































コメント