水圧

水圧

水圧の式 ・・・ $p_w=\rho hg$

ここで、$p_w$ : 水圧、$\rho$ : 水（流体）の密度、$h$ : 水深、$g$ : 重力加速度　です。

この式を導出してみましょう。

浮力についてはこちらを

浮力の式を導出する　動画あり

浮力については式を暗記して終わり！ということはないでしょうか？ 物体の体積 $V$ 、流体の密度 $\rho$ 、重力加速度 $g$ 、とすれば、 $$ F=\rho Vg$$ となります。 しかし、暗記した式に値を代入して「できました」、...

kokolainen.com

一般に、圧力 $p$ は、$圧力=\dfrac{力}{面積}$　の式で求めます。

水中での圧力は水深が同じであれば、全方向同じ大きさ（下図）であることから、鉛直下方について考えます。（方向により圧力が違うと、水中のある点を考えた場合、その点が動いてしまいます）

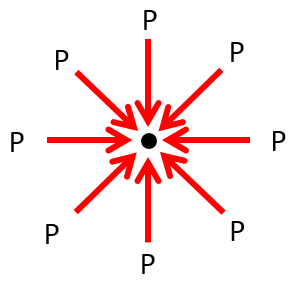
有名な「パスカルのハエ」など、このあたりの話については、

【動画解説】物理のエッセンス　熱力学 12番 P16

意外と浮力が圧力差により生じるということを忘れてしまいがちです。 そのため、余計な力を描いてしまったりするので注意が必要です。

kokolainen.com

も参照してください。

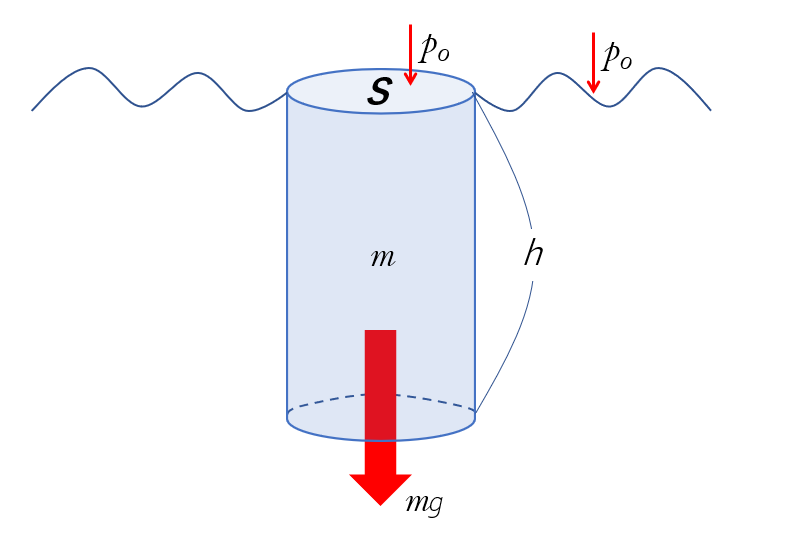
水深 $h$ での水による圧力を考える場合、断面積 $S$ で、高さ $h$ の水の円柱を考えます。
その円柱の重力による重さ $W$ は、水の円柱の質量を $m$ とすると、 $W=mg$　で示されます。

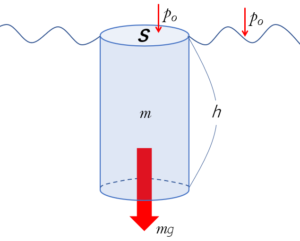
このとき円柱の底面で受ける力 $W$ を、その面積 $S$ で割ったものが、水深 $h$ での水圧 $p_w$ です。
よって、$p_w$ は、

$p_w=\dfrac{W}{S}$

と示されます。
ここで、$W=mg$　ですから、

$p_w=\dfrac{W}{S}$

$~~=\dfrac{mg}{S}$

水の密度を $\rho$ とすると、水の質量 $m$ 、水の体積 $V$ との関係は、$\rho=\dfrac{m}{V}$　です。したがって、 $m=\rho V$　として代入すると、

意外と、密度の理解があやふやな人が多いように思います。
密度がわからないと非常に困ります。
ここでしっかり、復習しておきましょう。

$p_w=\dfrac{mg}{S}$

$~~=\dfrac{\rho Vg}{S}$

ここで、水の柱の体積　$V=S\times h$　であるので、

$p_w=\dfrac{\rho Vg}{S}$

$~~=\dfrac{\rho Shg}{S}$

$p_w=\rho hg$

となり、これが水深 $h$ での水による圧力です。

気を付けてほしいことは、水深 $h$ で感じる圧力 $p$ は、水面が受ける大気圧 $p_0$ を足す必要があることです。

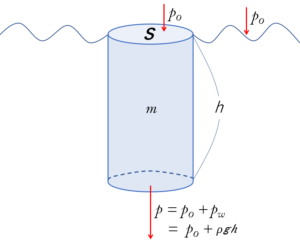
したがって、

$p=p_0+p_w$

$~~=p_0+\rho hg$

として示されます。

水圧はだいたい $10\:\mathrm{m}$ もぐると、1気圧増えます。
つまり、あなたが水中に潜ると、 $10\:\mathrm{m}$ で感じる圧力は、大気圧の 1 気圧 とあわせて 2 気圧 感じることになります。

これは、 $1\:\mathrm{cm^2}$ あたり約 $2\:\mathrm{㎏}$ の重りをのせているのと同じです。