物理のエッセンス 熱力学 12番 P16
物理のエッセンス 熱力学の16ページ12番を参照してください。
問題の概要
図のように筒を伏せたようにして水に浮かせています。
筒の中の水面までの長さ $l_1+l_2$
1 中の気体の圧力を求めましょう。
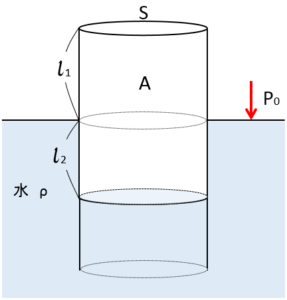
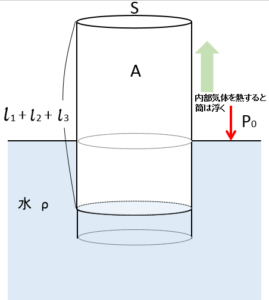
2 中の気体の温度を上げたとき、筒が浮いて、筒内部の上端から水面までの長さが $l_1+l_2+l_3$ になったとします。このとき気体がした仕事 $W’$ を求めます。
答え
動画解説
1
圧力を考えたとき
中の気体の圧力を $P_A$ とします。
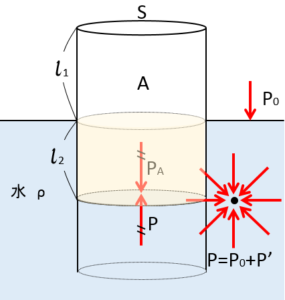
水面下 $l_2$ での水圧 $P’$ は、$P=\rho hg$ より、$P’=\rho l_2 g$
しかし、その地点での感じる圧力 $P$ は大気圧を足す必要があるので、
\begin{eqnarray}
P=P_A%=%P\\
&=&P_0+P’\\
&=&P_0+\rho l_2g
\end{eqnarray}
となることに注意してください。

これは漬物石を考えてみればよいでしょう。
漬物樽の中のナスビが感じる圧力は、漬物石が上に載っていれば大きくなります。
大気の重さはこの漬物石みたいなものだということです。
水圧の式は、あくまで水による圧力を計算しています。
別解 力のつり合いを考えたとき
筒に対する力のつり合いを考えてみます。
筒の浮力を考えるとき
筒全体を考えます。
よって、筒全体の重さ=浮力($\rho V g$) となります。
$$Mg=\rho (Sl_2)g$$
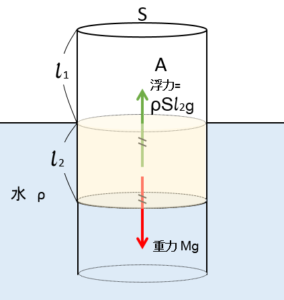
このとき、大気圧が筒上面を押しているなどとして・・・$+P_0S$ などを考えてはいけません。
筒が受ける圧力を考えるとき
筒だけを考えます。
よって、筒が受ける力として大気圧が押す力 $P_0S$ と内部の気体が筒を押す力 $PS$ 、そして筒が受ける重力 $Mg$ を考えると、つり合いの関係から、
$$PS=P_0S+Mg$$
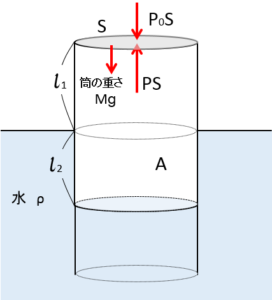
このとき、浮力を考えてはいけません。
これらの式、$Mg=\rho (Sl_2)g$、$PS=P_0S+Mg$ から $P=P_0+\rho l_2g$ を得ます。
なぜか?
このところは正しく理解できていないと間違える箇所です。
しっかりと理解しておきましょう。
例を見ながら考えていきます。
例
図を見てください。木片が水に浮いています。
大気圧 $P_0$ 、木片の水に沈んでいる部分を $l$ とします。
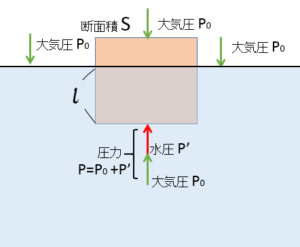
では、木片にはたらく圧力による合力 $F$ を考えてやりましょう。
$$F={(P_0+P’)S-P_0}S$$
で上向きの力がはたらくことがわかります。
ここで、水の密度 $\rho$ としてやると、$P’=\rho lg$ だから、
\begin{eqnarray}
F&=&(P_0+P’)S-P_0S\\
&=&P’S\\
&=&(\rho lg)S
\end{eqnarray}
ここで、$ l S=V $ であるから($V$ は水没している部分の体積)
$$F=\rho Vg$$
これは浮力の式ですね。
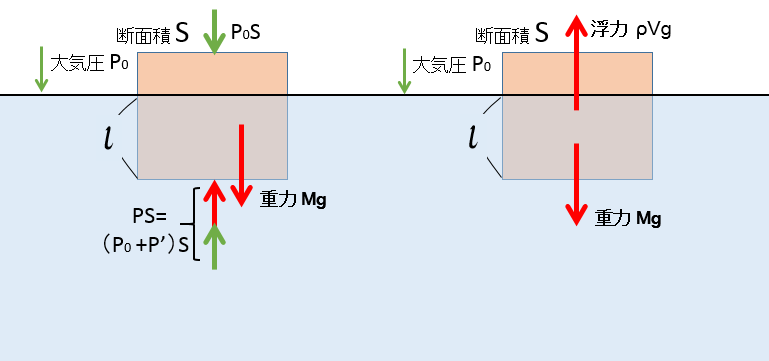
浮力で考えるのと圧力で考えるのは、同じことを違う面から見ている、ということです。
こういったことは、十分わかっているはずだと思っていても、直感にとらわれていたりするので注意が必要です。
したがって、この問題では、浮力を考えるときは圧力による力を考えず、また、圧力による力を考えるときは浮力を考えてはいけません。
その他、よくある勘違い
大気圧 $P_0$ の赤い矢印が図では上から下に向かっていますね。
しかし、筒の下で気体が水から受ける圧力 $P$ は上を向いています。

このとき、この2つの圧力の方向が違うので、大気圧を引いてしまう人が見えます。
こういった考え方は質点や剛体のつり合いを考えるときは正しいのですが、流体ではちがいます。
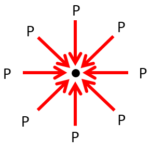
流体中のある1点を考えたとき、その点が受けるあらゆる方向からの圧力は同じ大きさです。(図)。これは流体の、移動変形する、という性質からきています。
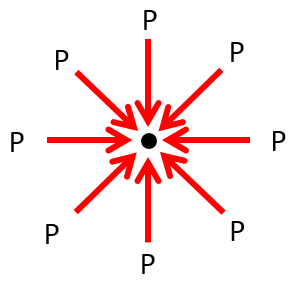
なぜなら、静止流体中で、このように圧力が相殺していないとすると、ある流体中の1点は静止せずに動いてしまうはずだからです。
したがって、問題の場合も水深が同じであれば、その地点での、あらゆる方向からの圧力は必ず同じ大きさになります。
つまり、筒の下面で水から受ける圧力は、同じ水中での深さ $l_2$ のところの圧力と等しいというわけです。
こぼれ話
パスカルが圧力について興味深い話をしています。
水を詰めた注射器にハエを閉じ込める。注射器の出口をふさぎ、満身の力を込めて注射器のピストンを押してもハエはつぶれない。
開放してやると、ハエは何事もなかったかのように飛び去った。
ハエを指先でつぶすのは簡単ですね。
しかし、水中では図のようにあらゆる方向からの圧力が等しい大きさをもつため、大きな力でピストンを押してもハエはつぶれないのです。圧力と圧縮は違うのです。
2
さて、筒の中の気体の温度を上げれば気体は膨張するでしょう。その結果、図のように筒が上昇して、筒内部の上部から水面までの長さが $l_1+l_2+l_3$ になっています。

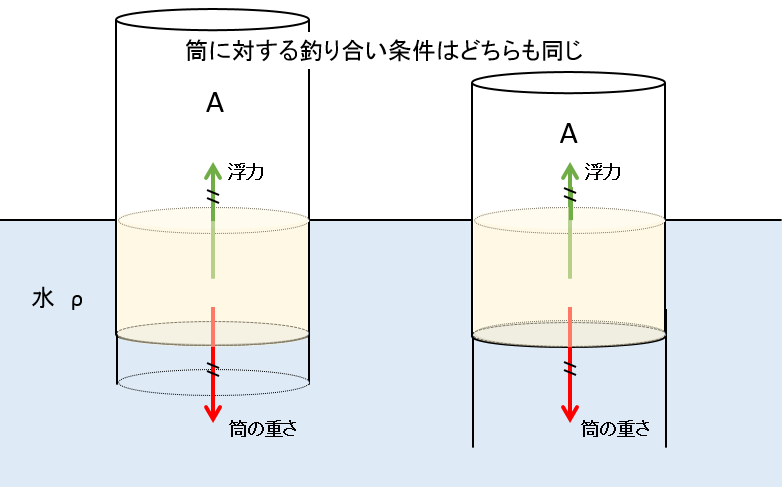
このときの筒が受ける力のつり合いを考えてみます。
筒全体の重さは、気体の温度をあげても変化しません。
どの状態でも筒は静止しています。
したがって筒全体にはたらく力は、はじめの状態と気体の温度を上げた状態で同じはずです。
すなわち、筒全体にはたらく重力=筒が受ける水からの浮力 です。
(筒内部の気体の圧力による力は内力として考えます。)
よって、筒の重さが変わらないので、それとつりあう浮力はどの状態でも一定のはずです。
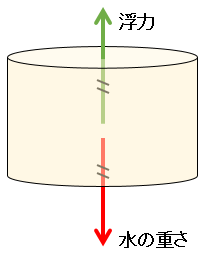
アルキメデスの原理によると、筒の受ける浮力は筒により押しのけられた流体(水)の重さに等しく、それは図の薄いピンクで示した部分の水の重さを意味しています。
すなわち、図の色をつけた円筒形の部分の体積はずーっと同じで、筒が上にスライドする、というイメージです。
したがって、$l_2$ の長さはいつも同じで、 $l_1$、$l_2$、$l_3$ は図のようになります。
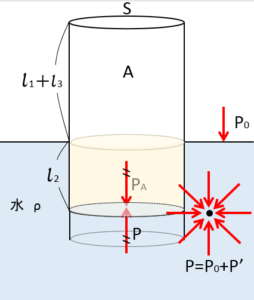
ゆっくりと筒が上昇したとすれば、圧力は一定とみなして良さそうですから、
$P_A=P=P_0 + \rho g l_2$ の定圧変化です。
定圧変化時の仕事は $W’=P\Delta V$ で示されます。
また、移動距離 $(l_2+l_3)-l_2=l_3$ 、筒断面積 $S$ より、$\Delta V=l_3\times S$ です。
よって、このときの気体のした仕事 $W’$ は、
$$W’=P\Delta V=(P_0+\rho g l_2)l_3S$$
となります。
最後までお読みいただき、ありがとうございます。
これからもよろしくお願いいたします。




































コメント