アインシュタインの示した有名な式 $E=mc\,^2$ をご存知でしょうか?
実はこの式を導くのは高校程度の物理の知識があれば可能です。
ここでは、一緒に導いてみましょう。
動画を追加しました!
高校物理でアインシュタインの特殊相対論

ParentRap / Pixabay
史上最も有名な物理の式・・といえばこの式をあげることに誰しも異論はないでしょう。
アインシュタインによるエネルギー $E$ と質量 $m$ についての式
$E=mc\,^2$
ここで $c$ は光速です。
光速は非常に大きい値ですから、上の式によるエネルギー $E$ は莫大な値を持つことがわかります。
動画で解説
エネルギーと質量は等価である
このシンプルで美しい式 $E=mc\,^2$ は何を示しているのでしょうか?
ためしに、質量に $m=1\:[g\:]=1\times 10^{-3}\:[kg\:]$ を代入してみましょう。
光速を $c=3.0\times 10^{8}\:[m/s\:]$ とします。
$E=mc\,^2$
$~~~=1\times 10^{-3}\times (3.0\times 10^{8})^2$
$~~~=9.0\times 10^{13}\:[J\:]$
となりました。
読み替えると、90兆ジュール。
この式の意味するところとは、もし $1\:[g\:]$ の物質のすべてをエネルギーに変換することができれば90兆ジュールのエネルギーを発生すると言っているのです。
つまり、この式は、質量はエネルギーに変換でき、その逆もできるということを示しているのです。
それでは、90兆ジュールとはどれほどのエネルギーでしょうか?
広島原子爆弾で変換された質量はどれくらいだったか

ご承知のように広島では世界で初めて原子爆弾が投下され多くの人が犠牲になりました。
このとき投下された爆弾はリトルボーイと呼ばれ、ウランを核分裂反応させたものです。
ちなみに長崎型原爆はプルトニウムを用いており、ファットマンと呼ばれていました。
| 55~63 兆ジュール | 広島型原子爆弾 ウラン |
| 63.1 兆ジュール | マグニチュード 6の地震エネルギー |
| 84~96 兆ジュール | 長崎に投下された原子爆弾 プルトニウム |
$1\:g$ の質量をエネルギーに変える事ができるとしたら90兆ジュールでしたね。
したがって表によると、だいたい長崎型原爆で約 $1\:g$ 、広島型原爆で約 $0.7\:g$ 程度の質量がエネルギーに変換されたことがわかります。
とてつもないエネルギーです。
思考実験で式を導く
 では式を導くため、次のような思考実験を行いましょう。
では式を導くため、次のような思考実験を行いましょう。
長さ $2L$ で、両端に質量 $M$の部分を持ち、簡単のため、その横部分は質量のない筒を考えます。
右端の質量 $M$ の部分から光子が照射され、左端の質量 $M$ の部分に向かいます。
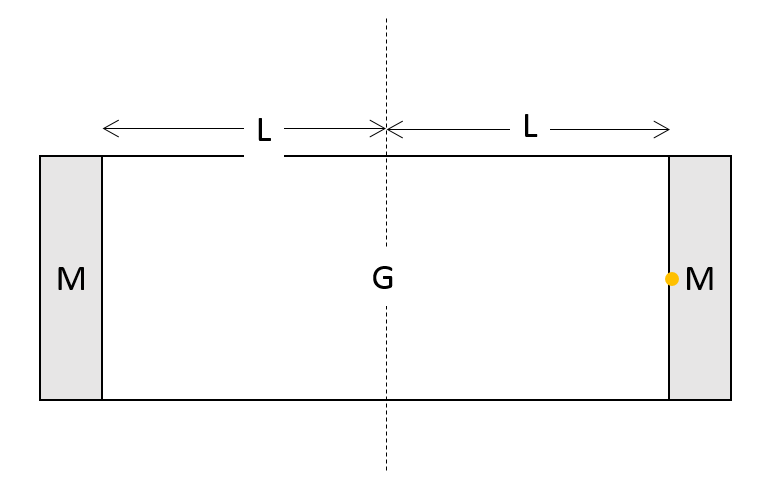
このとき、右端の $M$ のうち質量 $m$ だけがエネルギーに変換されて空間を伝わり、左端の質量 $M$ の部分に吸収され、質量 $m$ になったとしましょう。
光子が発射され、筒はその反動で図の右方向に速度 $v$ で運動したとします。
また、光子が右側から左側へ移動するまでの間に筒は $d$ だけ移動したとしましょう。
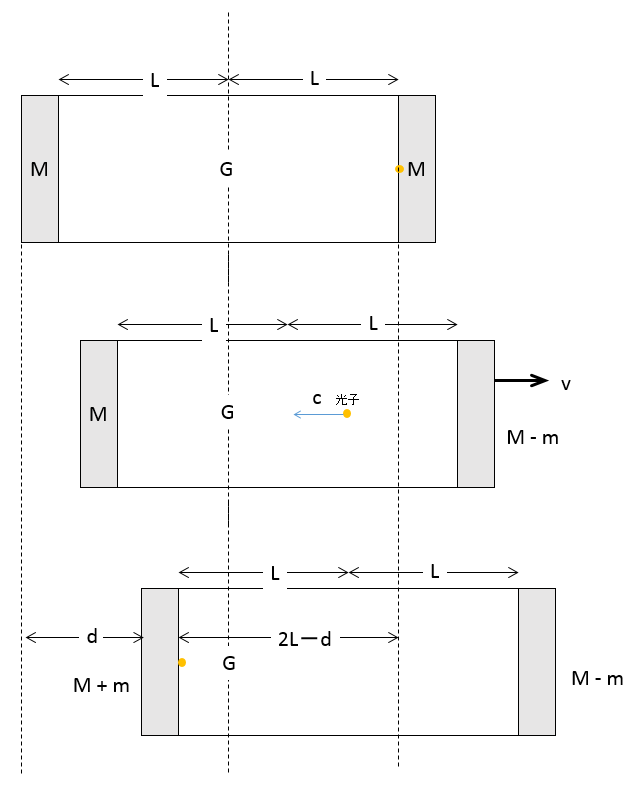
このとき、運動量保存法則により図の2つ目について次式が成り立ちます。
$ 0=Mv+(M-m)v-\dfrac{E}{c}\;\;\;\cdots \cdots(1)$

ここで光子エネルギーを $E$ とすると、光子運動量 $p$ は $p=\dfrac{E}{c}$ でしめされます。ただし、$c$ は光速です。
また、この筒の系においては、重心は光子の発射前と到着後で不動です。

系の重心が不動であることについては、次の記事を参照してください。
なるほど納得!分裂する物体の重心の位置
つまり重心はいつも $G$ にあるとして良いのですね。(真ん中の筒の系の重心は考えずとも良い)
以下に筒や光子の移動量を示したので確認して下さい。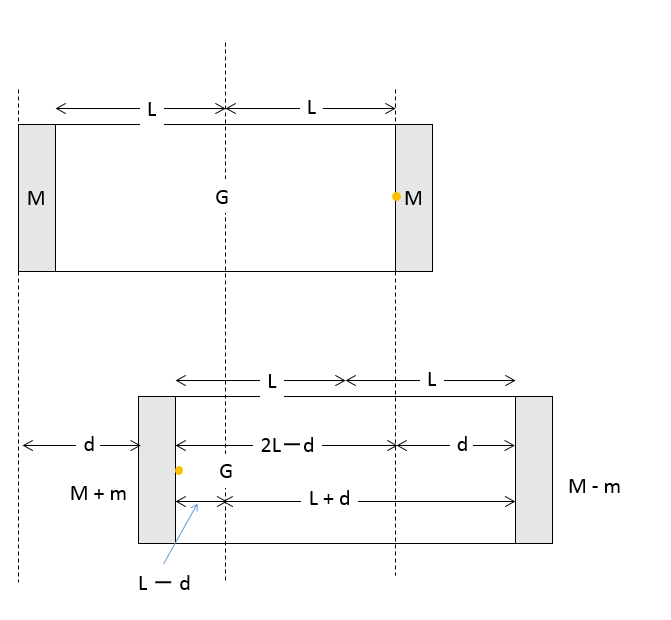
そして、この $G$ 周りのモーメントはつりあっているはずです。(モーメントというより重心ですが、まあ同じことです)
つまり、
$(M+m)\times(L-d)=(m-m)\times(L+d)\;\;\;\cdots \cdots (2)$
次に、光子は筒の右端から左端まで飛んだわけですから、光速 $c$ とした場合のその所要時間を $t$ とすると、
$(2L-d)=ct$
が成り立ちます。
さらに、筒はその間に右に速さ $v$ で距離 $d$ 移動したと考えられるので
$d=vt$
が成り立つことがわかります。
これらから、片々割って $t$ を消去すると、
$\dfrac{d}{2L-d}=\dfrac{v}{c}$
よって、
$v=c\times\dfrac{d}{2L-d}\;\;\;\cdots \cdots (3)$
が得られます。
では、$(1)$ より、
$E=(2M-m)\times c v$
と変形します。
次に、$(3)$ をこの式に代入して、
$E=(2M-m)\times c v$
$~~~=(2M-m)\times c \times c\times\dfrac{d}{2L-d}\;\;\;\cdots \cdots (4)$
$(2)$ を整理してみると
$Md=mL$
これを $(4)$ へ代入しましょう。
\begin{eqnarray}
E&=&(2M-m)\times c v\\\\
&=&(2M-m)\times c \times c\times\dfrac{d}{2L-d}\\\\
&=&\dfrac{2M-m}{2L-d}d\times c^2\\\\
&=&\dfrac{2Md-md}{2L-d}c^2\\\\
&=&\dfrac{2mL-md}{2L-d}c^2\\\\
&=&\dfrac{2L-d}{2L-d}mc^2\\\\
&=&mc\,^2\\\\
\end{eqnarray}
すなわち
$E=mc\,^2$
となります。
太陽などの恒星の莫大なエネルギー源は長い間不明でしたが、核融合反応により質量をエネルギーに変換して得ていると考えられます。
まとめ

質量とエネルギー等価の式 $E=mc\,^2$ は運動量保存とモーメントがわかっていれば導くことができます。
しかし、光量子仮説や光速度不変などの数々の天才的なひらめきとアイデアがあればこそですね。
最初にこういう考えに至るというのは、まさに天才の為せる技でしょう。






































コメント