交流回路の共振周波数 $f_0$ は、RLC直列・並列回路ともに次の式で示されます。
$f_0 = \dfrac{\omega_0}{2\pi} = \dfrac{1}{2\pi\sqrt{LC}}$
コイルインダクタンス $L$ コンデンサー電気容量 $C$
共振角周波数（角振動数） $\omega_0\:\: (=2\pi f_0) $
電磁気の記事は次を参照してください。
共振 交流の基礎8
RLC直列共振
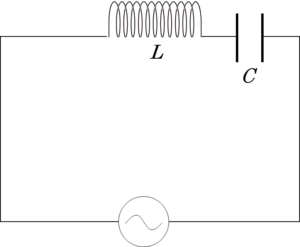
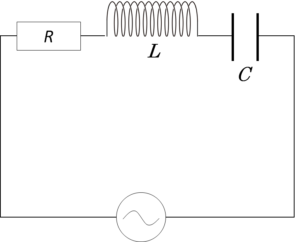RLC直列回路を考えます。
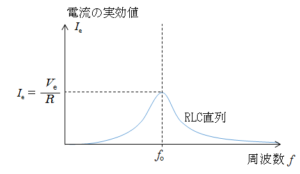
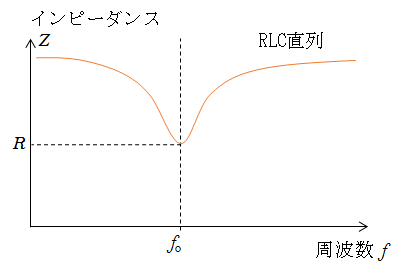
交流電源の電圧の周波数が共振周波数 $f_0$ のとき、回路に最大の電流が流れます。これが直列共振と呼ばれる現象です。
この共振周波数 $f_0$ は次の式で示されます。
$f_0 = \dfrac{\omega_0}{2\pi} = \dfrac{1}{2\pi\sqrt{LC}}$
コイルインダクタンス $L$ コンデンサー電気容量 $C$
共振角周波数（角振動数） $\omega_0=2\pi f_0$
これはRLC直列回路のインピーダンスから理解できます。
直列回路の場合の回路のインピーダンス $Z$ は次の式で示されます。（参照記事）
$ Z = \sqrt{ R^2+\left( \omega L \:- \dfrac{1}{\omega C } \right)^2 }$
このインピーダンスとはRLC直列回路における抵抗を示しています（ 単位 $\Omega$ ）。
また、回路全体の電圧・電流の最大値を $V_0$ 、$I_0$ とした場合、回路のオームの式から、
$I_0=\dfrac{V_0}{Z}$
したがって、 $Z$ 最小のとき回路の電流が最大になることがわかります。
$R$ が一定であるとき、$Z$ が最小になるのは、
$\left( \omega L \: – \dfrac{1}{\omega C } \right)=0 $
のときです。
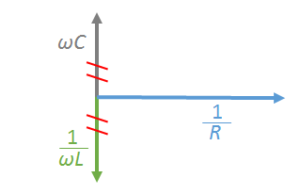
これは次のベクトル図で示した状態を意味しています。
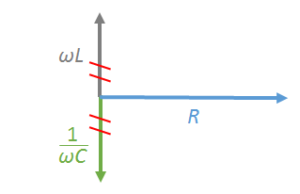
$\omega L$ と $\dfrac{1}{\omega C}$ が打ち消しあい、
力率は $\cos\phi=\cos 0 = 1 $ で最大になります。
このときRLC直列回路のインピーダンス $Z$ は $R$ に等しい。
（グラフは概略です）
これは見かけ上、コイルとコンデンサーが短絡しているように見えます。
ここで、共振時の $\omega$ を $\omega_0$ と書き換えて、
$\omega_0 L = \dfrac{1}{\omega_0 C }$
よって、
${\omega_0}^2 =\dfrac{1}{LC}$
$\omega_0 =\dfrac{1}{\sqrt{LC}}$
ここで $\omega_0 = 2\pi f_0$ だから
$\omega_0 = 2\pi f_0 = \dfrac{1}{\sqrt{LC}}$
ゆえに、
$f_0 = \dfrac{\omega_0}{2\pi} = \dfrac{1}{2\pi\sqrt{LC}}$
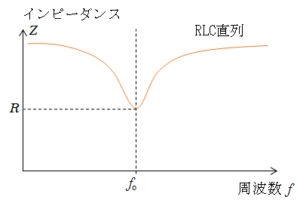
共振周波数 $f_0$ のとき、インピーダンスは $R$ で最小。
全体を流れる電流の実効値 $I_e$ は最大になります。（グラフは概略です）
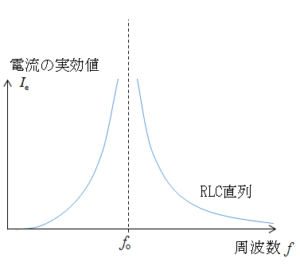
もしも、$R$ が 0 とみなせるようなときに、電源電圧の周波数が $f_0$ であれば、回路に非常に大きな電流が流れることになります。
（グラフは概略です）
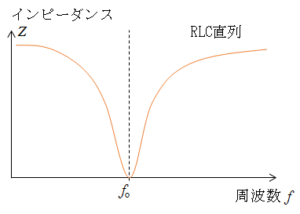
これは左図で示されます。抵抗 $R$ が 0 なのでインピーダンスが 0 になっています。
等速円運動や単振動は $\omega$ や $f$ などを理解するのに重要な単元です。
必要なら、もう一度復習をしておきましょう。
RLC並列共振
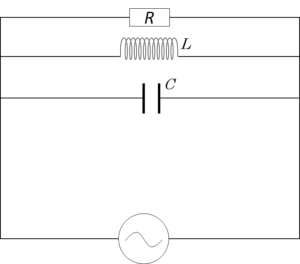
RLC並列回路を考えます。
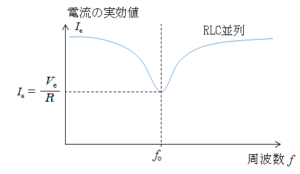
この場合も、共振現象が生じます。このとき、交流電源の電圧の周波数が共振周波数 $f_0$ のとき、全体を流れる電流が最小になります。これが並列共振と呼ばれる現象です。
この共振周波数 $f_0$ は次の式で表されます。
$f_0 = \dfrac{\omega_0}{2\pi} = \dfrac{1}{2\pi\sqrt{LC}}$
コイルインダクタンス $L$ コンデンサー電気容量 $C$
共振角周波数（角振動数） $\omega_0=2\pi f_0$
式の形は直列共振の場合と全く同じですね。
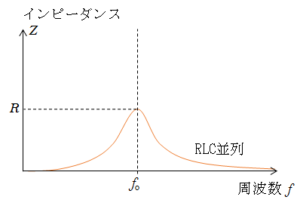
これもRLC並列回路のインピーダンスから理解できます。
並列回路の場合の回路のインピーダンス $Z$ は次の式で示されます。（参照記事）
$ Z = \dfrac{1}{\sqrt{ \dfrac{1}{R^2} + \left( \omega C \:- \dfrac{1}{\omega L } \right)^2 }}$
このインピーダンスとはRLC並列回路における抵抗を示しています（ 単位 $\Omega$ ）。
このとき、$R$ が一定である場合、 $\left( \omega C \: – \dfrac{1}{\omega L } \right) = 0 $ のときに $Z$ は最大で $R$ になります。
また、回路全体の電圧・電流の最大値を $V_0$ 、$I_0$ とした場合、オームの式から、
$I_0=\dfrac{V_0}{Z}$
したがって、 $\left( \omega C \: – \dfrac{1}{\omega L } \right) = 0 $ のとき $Z$ 最大で $R$ になり、回路全体を流れる電流が最小になります。（グラフは概略です）
よって、
$\left( \omega L \: – \dfrac{1}{\omega C } \right)=0 $
において、$\omega$ を $\omega_0$ と書き換えて、
$\omega_0 L = \dfrac{1}{\omega_0 C }$
よって、
${\omega_0}^2 =\dfrac{1}{LC}$
$\omega_0 =\dfrac{1}{\sqrt{LC}}$
ここで $\omega_0 = 2\pi f_0$ だから
$\omega_0 = 2\pi f_0 = \dfrac{1}{\sqrt{LC}}$
ゆえに、並列共振周波数は
$f_0 = \dfrac{\omega_0}{2\pi} = \dfrac{1}{2\pi\sqrt{LC}}$
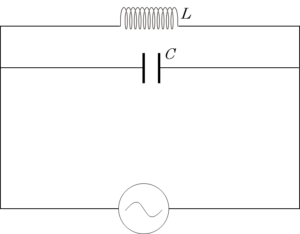
特に、並列に接続された抵抗のない LC並列回路では、電源電圧の周波数が $f_0$ になれば、回路のインピーダンスが $\infty$ になるため、回路に電流は流れなくなります。
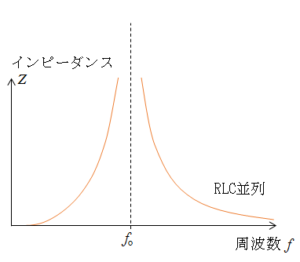
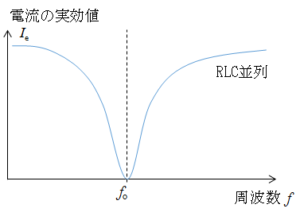
（グラフは概略です）
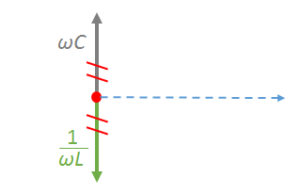
これは次のベクトル図で示されます。
インピーダンスは $\frac{1}{0} \rightarrow \infty$
電気振動・振動電流について
次の記事を参照してください。
コメント