RLC並列回路　交流の基礎6

交流のRLC並列回路について、インピーダンス、位相、などについて詳しく解説しています。

RLC並列回路　交流の基礎6 

関連記事です。

KoKo物理

物理のエッセンス解説 物理の クイズ 物理の 勉強方法 物理実験 過去問 YouTubeチャンネル 新！　2024年共通テスト物理解説　　 ワンポイント物理　このページ ・力学　・波動    ・熱力学　・電磁気 　・原子物理　・量子力学　・...

kokolainen.com

RLC並列回路

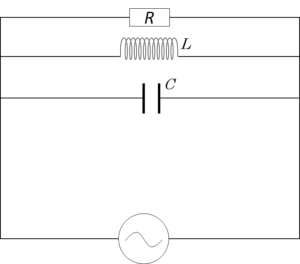
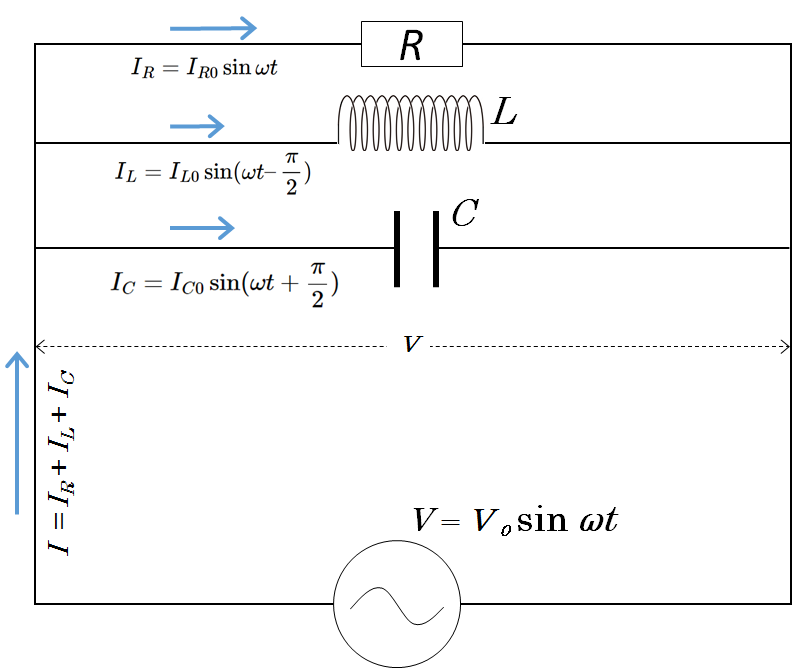
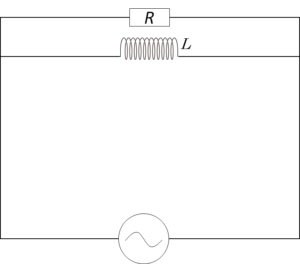
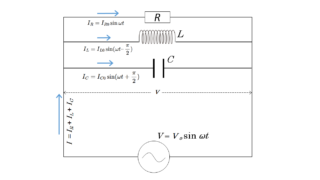
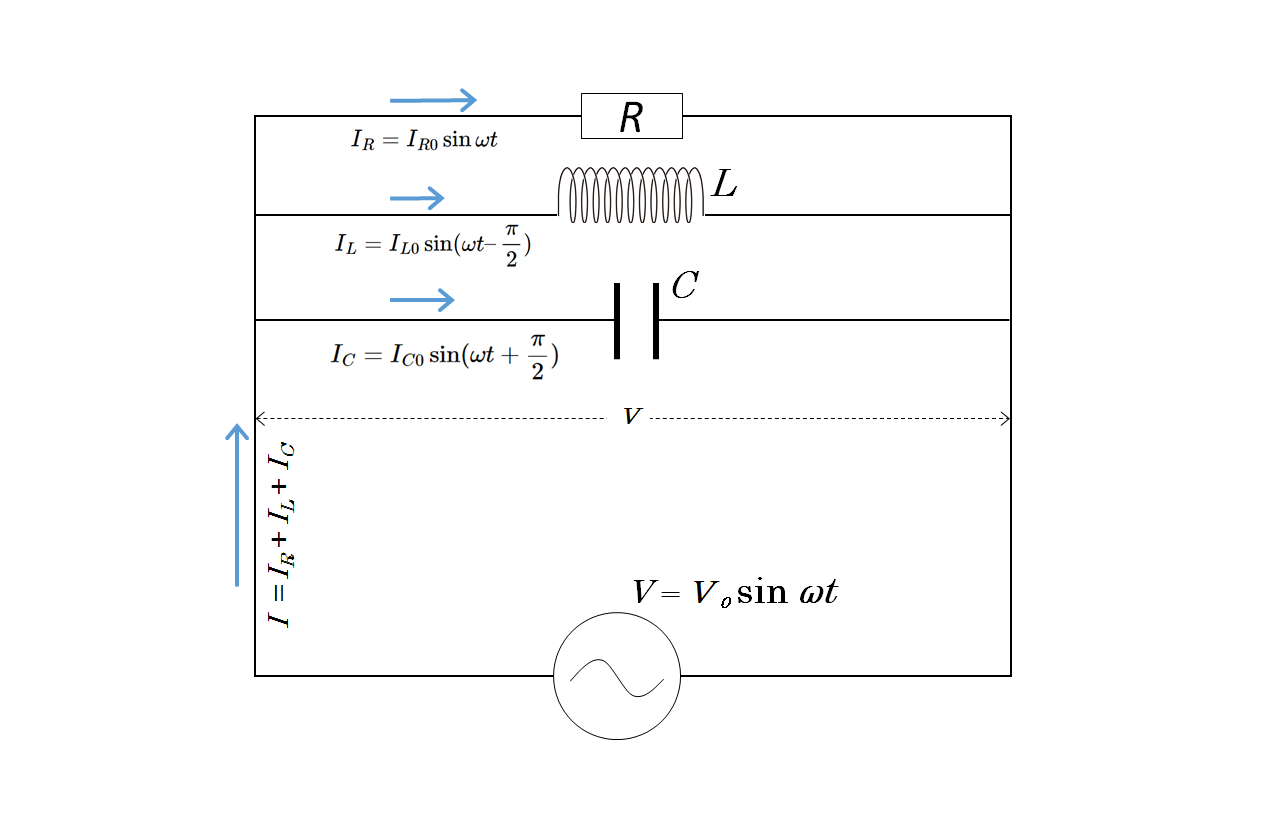
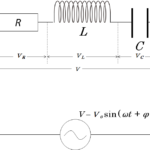
図のような、抵抗 $R$、 コイル $L$、コンデンサー $C$ からなる並列回路を考えます。この回路全体のインピーダンス $Z$ は次の式になります。

$Z=\dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left ( \omega C – \dfrac{1}{\omega L}   \right )^2}}$

また、回路全体にかかる電圧　$V=V_0\sin \omega t$　に対して、
回路全体を流れる電流　$I=I_0\sin (\omega t + \phi) $　とすると、

 

 

$\tan \phi = \dfrac{ \:  I_{C0} \: – I_{L0 }\:}{I_{R0}} = \dfrac{\:\omega C\: – \dfrac{1}{\omega L}   \: }{\dfrac{1}{R}}$

 

 

---

 

前回の直列回路（その１、その２）では直列のため、全ての素子に流れる電流は共通で同位相でした。

今回の並列回路ではそれぞれの素子に流れる電流は異なりますが、並列のため、電圧は共通で同位相になるはずです。

したがって、電圧を初期位相 0とし、 $V=V_0 \sin \omega t$　とおきます（ $V_0$ ： 最大値）。

 

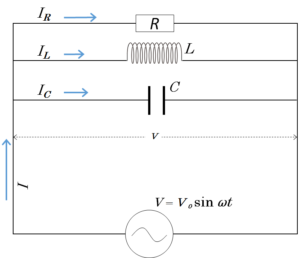それぞれの素子（抵抗、コイル、コンデンサー）を流れる電流を

• 抵抗 ･･･････････ $I_R$
• コイル ･････････ $I_L$
• コンデンサー ･･･ $I_C$

とします。

 

 

 

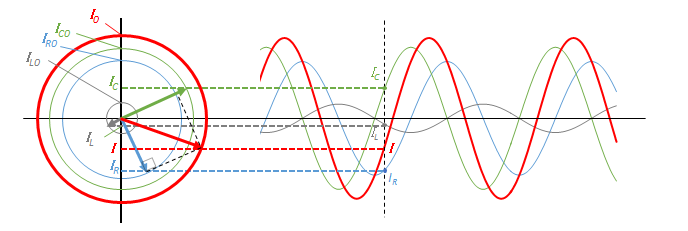
抵抗・コイル・コンデンサー に流れる電流

位相差

各素子を流れる電流を考えます。
各素子に共通の電圧がかかりますからそれを　$V=V_0\sin \omega t$　とした場合、電圧と電流に関しての位相のずれから、各素子を流れる電流は次のように書けます。

• 抵抗 $R$ を流れる電流 $I_R$ は、電圧　$V=V_0\sin \omega t$　と同位相
  　$I_R=I_{R0} \sin \omega t$

• コイル $L$ を流れる電流 $I_L$ は、電圧　$V=V_0\sin \omega t$　に対して $\dfrac{\pi}{2}$ 遅れている
  　$I_L=I_{L0} \sin (\omega t \: – \dfrac{\pi}{2})$　

• コンデンサー $C$ を流れる電流 $I_C$ は、電圧　$V=V_0\sin \omega t$　に対して $\dfrac{\pi}{2}$ 進んでいる
  　$I_C=I_{C0} \sin (\omega t  + \dfrac{\pi}{2})$

 

 

電流のグラフ

ここで各素子を流れる電流を縦軸に、時間を横軸にとったグラフを描きます。

電圧を　$V=V_0\sin \omega t$　としたとき、各素子の時間 $t$ に対する電流の値はそれぞれ、

• • $I_R=I_{R0} \sin \omega t$
  • $I_L=I_{L0} \sin (\omega t \: – \dfrac{\pi}{2})$
  • $I_C=I_{C0} \sin (\omega t  + \dfrac{\pi}{2})$

です。

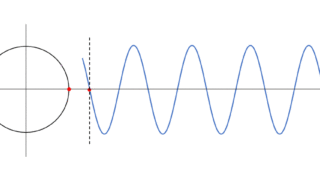
この $\dfrac{\pi}{2}$ の位相のずれとは、参考円において互いに 90° の角度差をもっているということです。
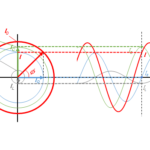
したがって、参考円での次の図のような等速円運動を考えます。

その際に、各参考円の半径は各素子に流れる電流の最大値（ $I_{R0}$  $I_{L0}$   $I_{C0}$ ）となります。　
これらのベクトルが図のように位相差を保ちながら、等速円運動している状態を考えます。
（注：ここでの図における各電流の大きさは適当です。図ではコンデンサーを流れる電流 ＞ コイルを流れる電流　となっています。）

 

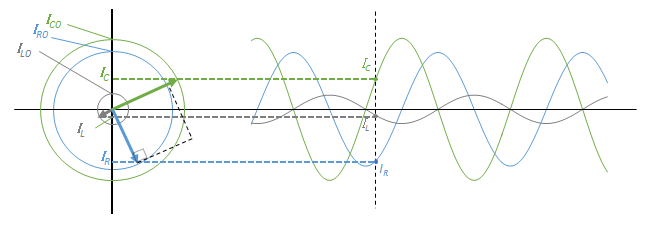
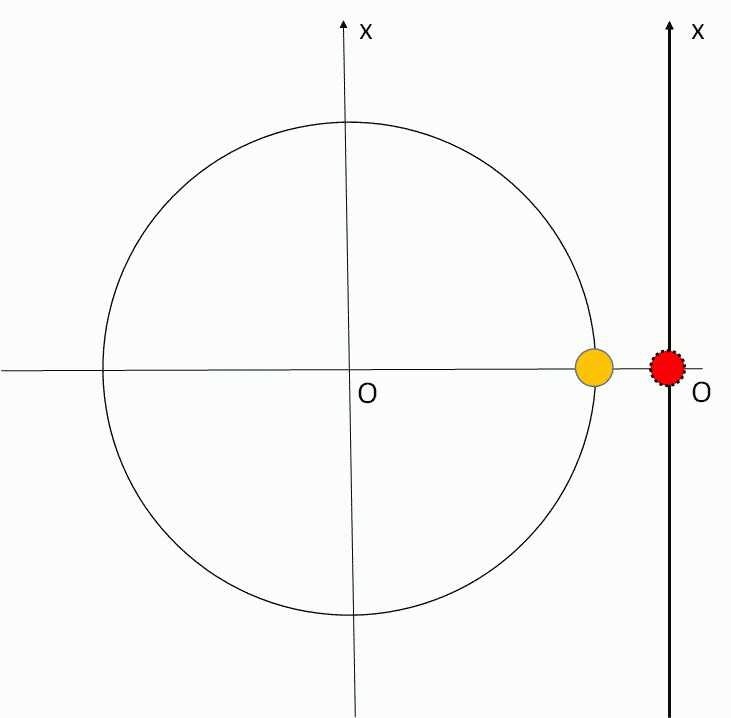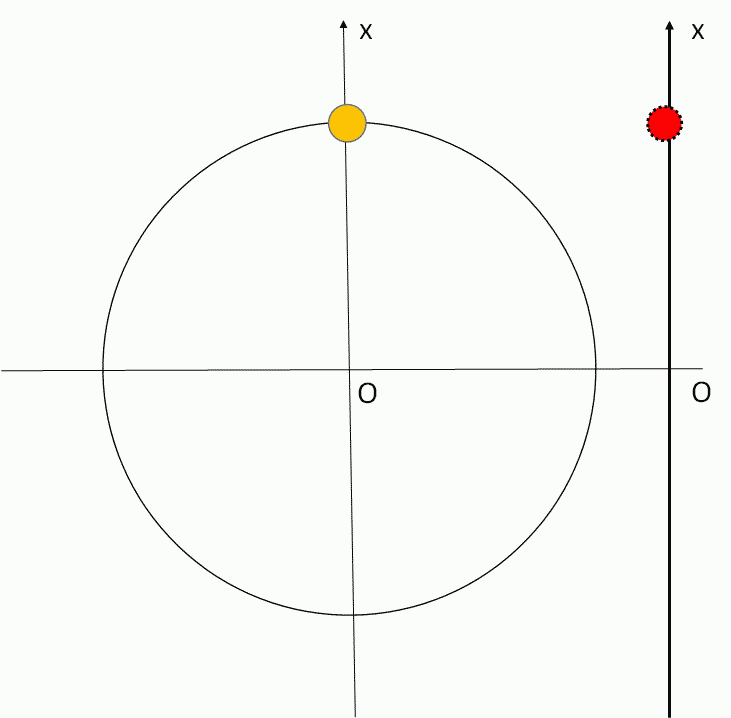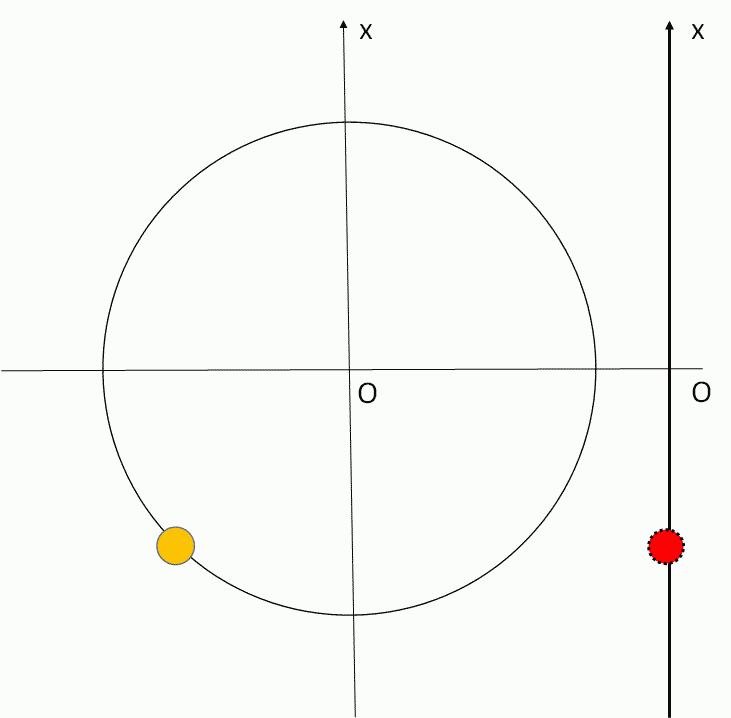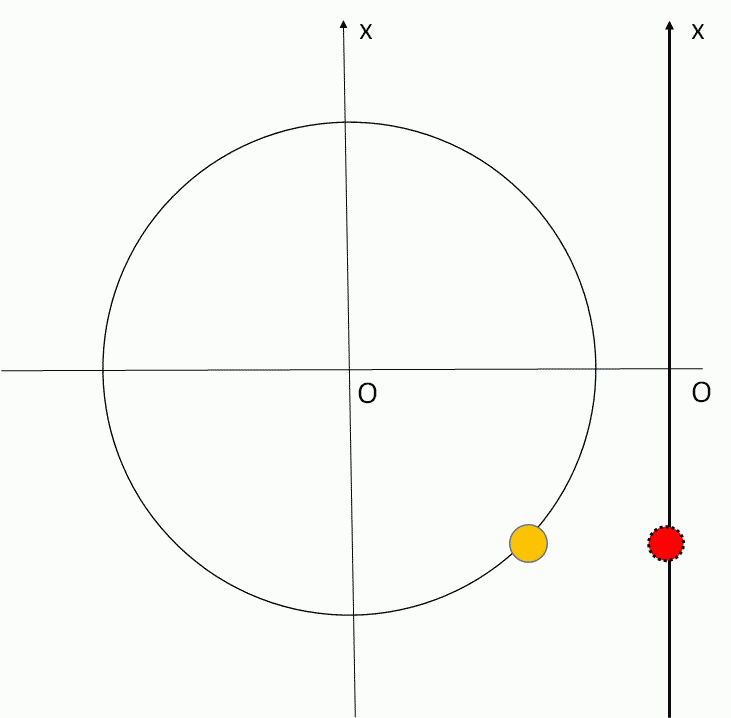
ここで、ある時刻 $t$ における回路全体を流れる電流を示すものは、参考円において各素子を流れる電流を合成したもの（図の赤色の部分）に等しくなります。

$I=I_R+I_L+I_C$

インピーダンス

コイル $L$ とコンデンサー $C$ の位相差はちょうど $\pi$ です。
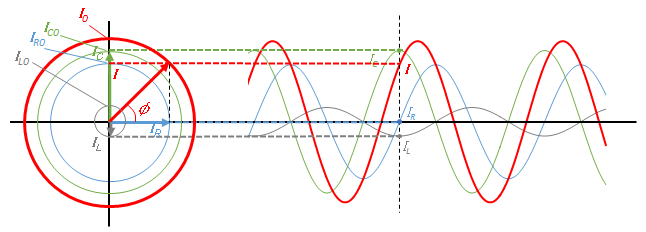
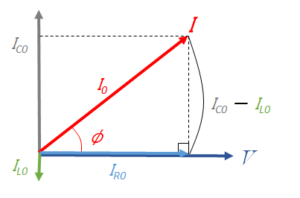
イメージをつかみやすくするために、回転して次の図のようになったときを考えます。 

 

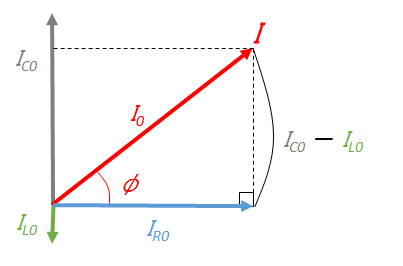求める $I$ の大きさは図で、

ピタゴラスの定理から

$I^2_{0}={I_{R0}}^2+(I_{C0 } \:- I_{L0})^2$

$I_{0}=\sqrt{{I_{R0}}^2+(I_{C0} \:- I_{L0})^2}$

となります。

 

さて、ここで各素子のオームの式

• $I_{R0}=\dfrac {V_0}{R}$
• $I_{L0}=\dfrac{V_0}{\omega L}$
• $I_{C0}=\omega CV_0$

 

であることから、これらを $I_0$ の式へ代入します。（ $V$ は RLC に共通です）

$I_{0}=\sqrt{{I_{R0}}^2+(I_{C0} \:- I_{L0})^2}$

$~~~~=\sqrt{ \left ( \dfrac {V_0}{R} \right )^2 + \left( \omega CV_0 \: –  \dfrac{V_0}{\omega L} \right)^2 }$

$I_0=\sqrt{\dfrac {1}{R^2} + \left( \omega C \: – \dfrac{1}{\omega L} \right)^2 }\:\:V_0$

 

実効値の場合も同様に考えて、

• $I_{Re}=\dfrac {V_e}{R}$
• $I_{Le}=\dfrac{V_e}{\omega L}$
• $I_{Ce}=\omega CV_e$
• $I_{e}=\sqrt{{I_{Re}}^2+(I_{Ce} \:- I_{Le})^2}$
• $I_e=\sqrt{ \dfrac {1}{R^2} + \left( \omega C \: – \dfrac{1}{\omega L} \right)^2 }\:\:V_e$

 

ここで、$\dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left ( \omega C – \dfrac{1}{\omega L}   \right )^2}} = Z $　とおきます。
そうすると、

 

• $I_0=\dfrac{V_0}{Z}$   
  　　　
• $I_e=\dfrac{V_e}{Z}$   

 

となり、オームの式　$I=\dfrac{V}{R}$　と同じ形です。
そこで、この $Z$ を交流回路における抵抗をあらわす値と考え、$Z$ をインピーダンスと呼ぶことにします(単位 $\Omega$ )。

位相差

今回は、電圧を　$V=V_0 \sin \omega t $　としています。
回路全体にを流れる電流は、電圧との位相のずれを $\phi$ として、
$I=I_0\sin (\omega t + \phi) $　と考えられます。

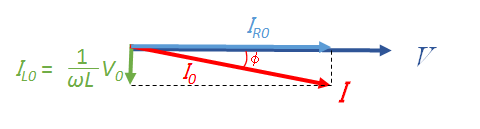
 電圧 $V$ の位相と抵抗を流れる $I_{R}$ の位相は等しいため、図の角度 $\phi$ が電圧 $V$ に対する、回路全体を流れる電流 $I=I_R+I_L+I_C$ の位相のずれを示していることになります。

 

 

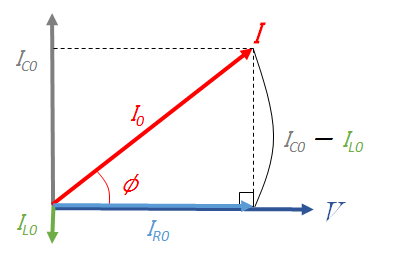図より、RLC並列回路にかかる電圧 $V$ と回路全体を流れる電流 $I$ の位相差 $\phi$ は、

$\tan \phi = \dfrac{ \:  I_{C0} \: – I_{L0 }\:}{I_{R0}}$

$~~~~~~~~~ = \dfrac{\: \omega C \: – \dfrac{1}{\omega L} \: }{\dfrac{1}{R}}$

となります。

 

LC並列回路　RC並列回路　RL並列回路

• LC並列回路

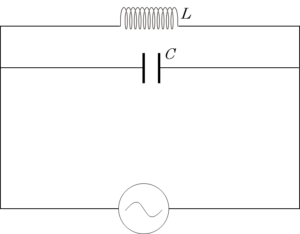さて、RLC並列回路において、抵抗 $R$ がない場合はどうなるでしょうか。その場合は、単に式から抵抗に関する部分を消去すればOKです。

 

 

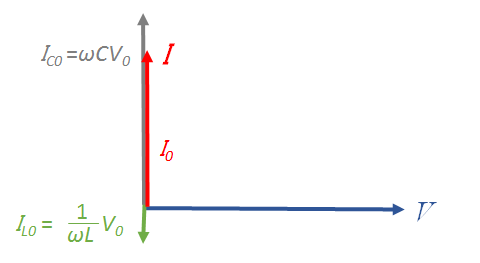
$Z = \dfrac{1}{\sqrt{\left ( \omega C – \dfrac{1}{\omega L}   \right )^2}}  $

$~~~= \dfrac{1}{\left | \omega C – \dfrac{1}{\omega L}   \right |}$

この場合の位相は、$\omega C$ と $\dfrac{1}{\omega L}$ の大きいほうを向きます。

 

もし $\omega C$ と $\dfrac{1}{\omega L}$ が同じ大きさのときはインピーダンス $Z$ が $\infty$ になり、電流が流れません。これについては共振の記事で解説します。

 

同様に

• RC並列回路

     

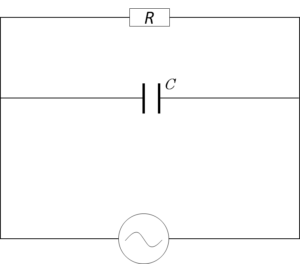
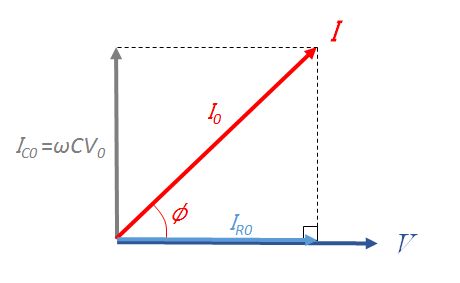
$ Z = \dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left ( \omega C  \right )^2}}  $

 

• RL並列回路

      

$ Z = \dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left ( – \dfrac{1}{\omega L}   \right )^2}}  $

まとめ

抵抗を流れる電流 $I_R$　　コイルを流れる電流 $I_L$　　コンデンサーを流れる電流 $I_C$ とする。

各素子を流れる電流の最大値と実効値をそれぞれ以下の式で示す。

• 回路全体･･････最大値 $I_0$      実効値 $I_e$
• 抵抗･･････････最大値 $I_{R0}$    実効値 $I_{Re}$
• コイル････････最大値 $I_{L0}$    実効値 $I_{Le}$
• コンデンサー･･最大値 $I_{C0}$    実効値 $I_{Ce}$

 

RLC（LCR）並列回路においては、回路全体にかかる電圧を　$V=V_0\sin \omega t$　とした場合、各素子を流れる電流は

• $I_R=I_{R0} \sin \omega t$
• $I_L=I_{L0} \sin (\omega t \: – \dfrac{\pi}{2})$
• $I_C=I_{C0} \sin (\omega t + \dfrac{\pi}{2})$

 

• $I_{R0}=\dfrac {V_0}{R}$
• $I_{L0}=\dfrac{V_0}{\omega L}$
• $I_{C0}=\omega CV_0$

 

• $I_{Re}=\dfrac {V_e}{R}$
• $I_{Le}=\dfrac{V_e}{\omega L}$
• $I_{Ce}=\omega CV_e$

 

$I=I_R+I_L+I_C$

 

• $I_{0}=\sqrt{{I_{R0}}^2+(I_{C0} \:- I_{L0})^2}$
• $I_0=\sqrt{\dfrac {1}{R^2} + \left( \omega C \: – \dfrac{1}{\omega L} \right)^2 }\:\:V_0$

• $I_{e}=\sqrt{{I_{Re}}^2+(I_{Ce} \:- I_{Le})^2}$
• $I_e=\sqrt{ \dfrac {1}{R^2} + \left( \omega C \: – \dfrac{1}{\omega L} \right)^2 }\:\:V_e$

 

この $Z$ を交流回路における抵抗成分と考え、インピーダンスと呼びます。

$I_0=\dfrac{V_0}{Z}$

$I_e=\dfrac{V_e}{Z}$ 

$ Z = \dfrac{1}{\sqrt{\dfrac{1}{R^2}+\left ( \omega C – \dfrac{1}{\omega L}   \right )^2}} $

 

RLC並列回路にかかる電圧と回路全体を流れる電流の位相差 $\phi$ は、

$\tan \phi = \dfrac{ \:  I_{C0} \: – I_{L0 }\:}{I_{R0}} = \dfrac{\: \omega C \:  – \dfrac{1}{\omega L}  \: }{\dfrac{1}{R}}$

 

RLC直列回路・RLC並列回路　ともに基本をしっかり理解できればおそるるに足りません。