交流とコンデンサー 交流の基礎 4
交流回路は難解な単元といわれますが、段階を追って学んでいけば恐るることはありません。
電磁気の記事は次を参照してください。

交流とコンデンサー
交流とコンデンサーの関係について解説します。
コンデンサーの両極板間は絶縁されていますので、回路的には切れています。
しかし、交流回路では両極版にたまる電荷の正負が激しく入れ替わるため、コンデンサーは交流電流を通しているように振舞います。電源の周波数が高いほど交流電流を通しやすく、この性質はコイルとは正反対です。
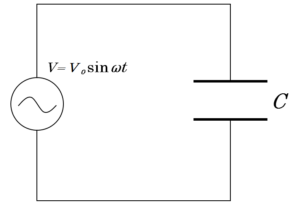
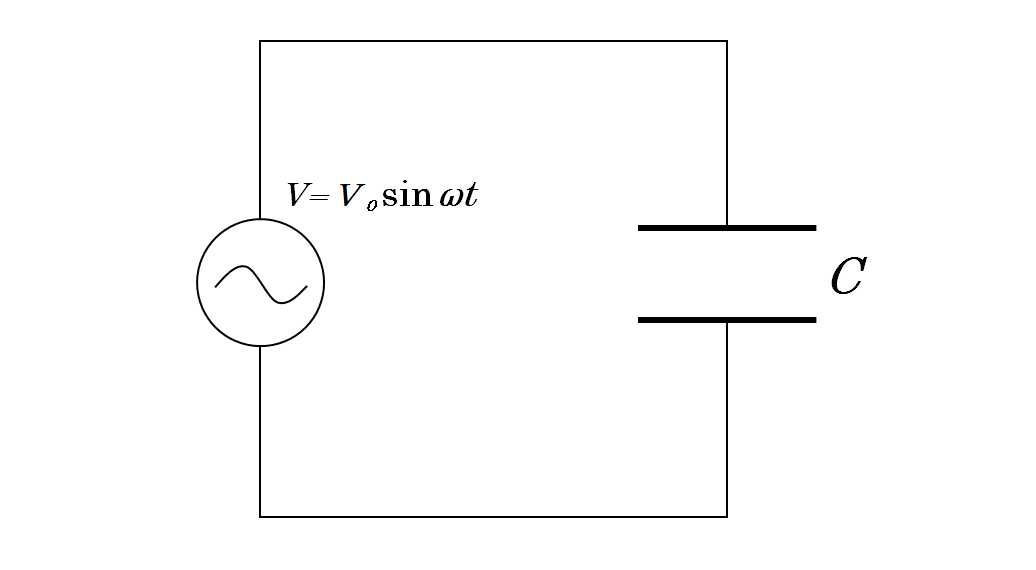
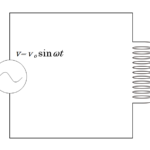
交流電源とコンデンサーをつないだだけの回路を考えます。
電源電圧は $V=V_0\sin \omega t$ で変化し、コンデンサーの電気容量を $C$ とします。
コンデンサーに蓄えられる電気量 $Q$ と電圧 $V$ 、電気量量の関係式は
$Q=CV$
電流の定義は $I=\dfrac{\Delta Q}{\Delta t}\:\Longrightarrow\:\dfrac{\mathrm{d} Q}{\mathrm{d} t}$
したがって、 $Q=CV=C(V_0\sin \omega t)$ および、コンデンサーに流れる電流を $I_C$ として、
$I_C=\dfrac{\mathrm{d} Q}{\mathrm{d} t}$
$~~~=\dfrac{\mathrm{d}}{\mathrm{d} t}(CV_0\sin \omega t)$
$~~~=\omega C V_0 \cos \omega t$
$I_C=\omega C V_0 \sin( \omega t + \dfrac{\pi}{2})$

$\cos \omega t = \sin(\omega t + \dfrac{\pi}{2})$
ここで電流の最大値 $I_0=\omega C V_0$ とおけます。
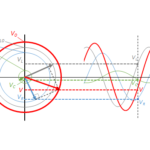
位相のずれ
これと、電源電圧の式 $V=V_0 \sin \omega t$ とを比較します。
とくに $\sin$ の中(位相)に注目します。
$V=V_0 \sin \omega t$
$I_C=\omega C V_0 \sin( \omega t + \dfrac{\pi}{2})$
そうすると、 コイルを流れる電流 $I_C$ は電源に比べて、位相が $\dfrac{\pi}{2}$ だけ進んでいることに気がつきます。
リアクタンス
ここでオームの法則( $V=RI$ )を思い出してみます。
$I=\dfrac{V}{R}$
$I_C=\omega C V_0 \sin( \omega t + \dfrac{\pi}{2})$
これらの式をじっくりと見ます・・・。
そうすると、オームの法則で示される抵抗 $R$ と同じ働きをするものがあることに気がつきます。
すなわち、
$ \omega C \: \Longrightarrow \:\dfrac{1}{R}$
よって、コイルをつないだ回路の抵抗成分 $X_C$ として
$X_C =\dfrac{1}{\omega C}$
とし、この抵抗成分 $X_C$ をリアクタンスと呼ぶことにします。
まとめ
位相
コンデンサーを流れる電流の位相は、電圧の位相に対して $\dfrac{\pi}{2}$ 進んでいる。
これを言い換えると、
コンデンサーにかかる電圧の位相は、コンデンサーを流れる電流の位相に対して $\dfrac{\pi}{2}$ 遅れている。
とも書けます。これらはコイルの場合と逆ですね。
リアクタンス
交流回路におけるコイルの抵抗成分をリアクタンス $X_C$ とよび、
$X_C =\dfrac{1}{\omega C}$
で示される。
リアクタンス $X_C$ の値は $\omega$ や $C$ が大きいほど小さくなることがわかります。
$\omega = 2\pi f$ ですから、周波数の大きい電源ほどコンデンサーの抵抗成分は小さくなります。




































コメント