フランスのルイ・ド・ブロイをご存知でしょうか?
量子力学の黎明期に活躍した物理学者の一人でノーベル物理学賞を受賞しています。
受賞理由は「電子の波動性の発見」(1929)です。

波動性と粒子性
波動性とはどういう意味でしょうか?
波動性に対する語としては粒子性があげられます。
イメージとしては、波動性は文字通り海の波のようなものです。
対して粒子性とは、野球のボールを想像していただければいいと思います。
われわれの常識では、これら二つの現象は日常生活では共存し得ないものです。
そもそも電子は質量が $9.1\times 10^{-31}\: \mathrm{kg}$ である粒子だと考えられていました。
ド・ブロイの主張は、従来粒子であることに対して疑いのなかった電子に波動性を発見したというのです。
どういうことか詳しく見ていきましょう。
話は光の話にさかのぼります。
光電効果の実験
19世紀も終わる頃、一つの論文が提出されました。それが光電効果と呼ばれる現象に関するものです。
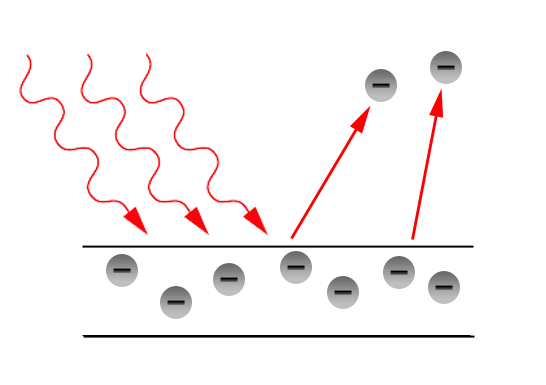
光電効果とはよく磨いた金属板に光を当てると電子が飛び出すという現象です。
この光電効果という現象が発見された当時、これを古典的な波動論ではうまく説明できませんでした。
当時の科学者たちは少し困難ではあるがそのうち解決されるはず・・と思っていたのです。何しろ、ニュートン力学とマックスウェルの電磁気学により物理現象はすべて解明された・・・と考えられていたからです。
しかし、光電効果については一向に解決されなかったのです。
そんななかアインシュタインは光電効果に関する論文を目にします。
アインシュタインは論文を読んだときおそらく直感的に「ここにはなにかある」と思ったのに違いありません。
早速その解明に取り掛かります。

ところで、光は回折や干渉という波動特有の現象を示します。
当時、光の干渉や回折をしめしたヤングの実験などにより、光は波動であるという考え方が主流でした。
ところが、アインシュタインは
- 光は光子(フォトン)と呼ばれる粒子からなる
- 振動数 $\nu$ の光子のエネルギーは、$E=h\nu$ ($h$ はプランク定数)で示される
- 一つのフォトンが一つの電子に作用する
と仮定したのです。
光電効果の詳しい説明は他の記事に譲りますが、ここでは従来、波と考えられていた光が粒子としての性質をもつのだ、ということに気をつけてください。
アインシュタインは光の粒子性を考えて見事に光電効果の説明に成功します。
そして、アインシュタインはこの功績によりノーベル物理学賞を受賞しました。
(相対性理論ではありません)
こちらも参考に(物理のエッセンスの光電効果等、原子分野を解説しています)

電子の波動性
従来、波であると考えられていた光に粒子としての性質が見つかったのです。
では、粒子と考えられていたものに波動性があってもいいのではないか?
そう考えた男がいました。
ド・ブロイは彼の博士論文で従来、粒子として考えられていた電子には逆に波動性があるのではないかという考えを示したのです。
それは当時、あまりにも革新的な考え方でもあったためか、しばらく理解されませんでした。
指導教官たちはド・ブロイの論文をアインシュタインに送って意見を求めています。
アインシュタインは「この男には博士号よりノーベル賞がふさわしい」と返答したという話が残っています。
そして、ついに電子の波動性を認めざるを得ないような実験が行われます。
デビソン・ガーマーらによる電子による回折実験です。
この実験はニッケルの結晶に電子を照射するとその干渉模様が得られたというものです。
干渉・回折が得られるということは波動性をもつことを示しています。
すなわち、粒子である電子に波動性があることが確定的になったのです。
それでは式を確認していきましょう。
まず、光量子仮説から光子 1 個のもつエネルギーは、$E=h\nu$ で示されます。
ただし、$h$ はプランク定数、$\nu$ は振動数です。
光子の運動量 $p$ は、$p=\dfrac{E}{c}=\dfrac{h\nu}{c}=\dfrac{h}{\lambda}$ となります。$(c=\nu \lambda)$
光子は粒子だといいながら波長 $\lambda$ が入っていますね。
これを変形して、波長 $\lambda$ は、$\lambda=\dfrac{h}{p}$ で」示されることになります。
ここで電子を考えます。
電子の質量 $m$、速度を $v$ としてやると、電子の運動量は $p=mv$ です。
これを先程の光子の式に代入してやります。
そうすると、
$\lambda=\dfrac{h}{mv}$
が得られます。これは電子の運動に伴う波を示しているのです。ただ、この波の正体については今のところ良くわかっていないといったほうがいいようです。
しかし、とにかくこの波が実際に観測され、それを活かした器具も開発されています。
電子顕微鏡です。
電子顕微鏡は光のかわりに電子波を用いているものです。
電子は電荷をもつため電磁気力によりコントロールができます。電磁レンズという仕組みにより、電子線をつかって対象物を拡大できるのです。
先程の電子波の波長の式、$\lambda=\dfrac{h}{mv}$ からわかるように、電子の速度 $v$ を上げてやることで波長を短くでき顕微鏡の分解能を上げることができます。
物質波

粒子である電子に波の性質があるのなら・・・・そうですね。
粒子である陽子や中性子といったものにも波動性があるのではないか?・・と考えられます。
現在ではすべての粒子には波動性があることがわかっており、これを物質波と呼んでいます。
そうすると、世の中のすべて物は波動性を持つといっても良いことになります。
われわれも波でできているといってもいいことになりますね。








































コメント