電場と電位、電気力線などについて正確にきっちりと理解しましょう。
それが、電磁気理解の近道です。
多くの場合、こういう語句などの基礎概念をないがしろにした結果、往々にして
「教科書や参考書の言っていることが何のことやらさっぱりわからず」
という事態を招きます。
専門用語の理解は多くの人が思っているよりも重要なことです。
専門用語で意味のわからない単語が出てきたら、それはあなたにとってチャンスです。
かならずその用語について調べて自分のものにしましょう。
それでは今回は、一様な電場と電位について解説していきます。
一様な電場と電位
一様な・・・という言葉はどういう意味でしょうか?
辞書を引いてみました。
一様な・・・・全部同じようすであること。また、そのさま。同様。
とあります。
つまり一様な電場とは「全部同じようすをしている電場」ということになります。
電場を表すためには電気力線をイメージすれば簡単でしたね。この記事を参照
以下、電気力線との関係を考えて「一様な電場」について考えていきましょう。
一様な電場は普通の電場とどう違うのか 電気力線との関係
普通の電場・・・というのはちょっと曖昧ですが、次のような点電荷による電場を考えてみます。
このとき電気力線は図のようになります。
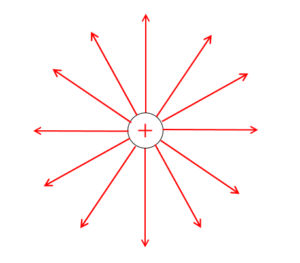
この電気力線の様子は一様でしょうか?
先程も書いたように、
一様な電場とは「全部同じようすをしている電場」
を意味します。
そして、電気力線は電場の様子を表しています。
しかし、図の電気力線は電荷に近いところでは密であり、遠くなるにつれて疎(まばら)になっていることがわかります。
これでは電気力線は一様であるとは言えません。
したがって、この場合の電場も一様ではありません。
では一様な電場での電気力線はどのように表されるのでしょうか。
一様な電場の例を示します。
たとえばコンデンサーのように金属板を向かい合わせた状態を想像します。
このとき、金属板の面積は十分に広いものとします。
(この十分に広い・・・というのが曖昧ですが、気になるなら無限に広いと思っておいて下さい)
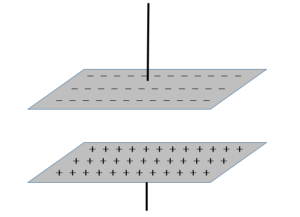
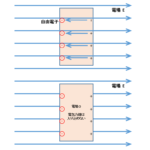
このとき、コンデンサー内部の電気力線を想像すると次の図のようになるはずです。
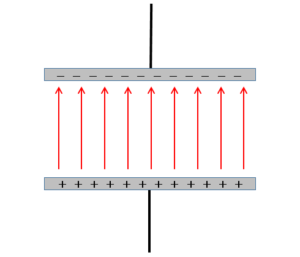

この電気力線の様子が納得いかない人は、
内部に正電荷をおいてそれが動く方向を
イメージしてみて下さい。
たとえば、下の正の極板に置かれた正電荷は
全てまっすぐに上の極板に向かうはずです。
厳密に言うと、極板の端では曲がることも
考えられますので、「十分に広い極板」
という表現をします。
このとき、電気力線は「一様」である・・・と言っても良いように思いませんか?
「電気力線が一様である」ということはその電場も一様であるという意味になります。
なぜかというと、電場の大きさ $E$ のところでは $E\:\mathrm{ 本/m^2}$ の電気力線を引くと約束しているからです。
これを理解するには次の図が参考になります。
$1\:\mathrm{ m^2}$ の網を用意して、網にかかる電気力線の本数を数えます。
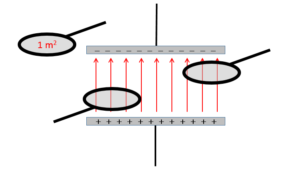
$1\:\mathrm{ m^2}$ の網で電気力線を捉えると、このコンデンサー内ではどこをとっても同じ本数の電気力線がえられます。
また、電気力線は互いに平行であることが明らかですから、この場合は「一様な電場」が形成されていると言えるのです。
電場は電位の高い方から低い方へ向く
さて、電場の向きですが、これは電気力線の向きと一致しています。
というか、そのように電場と電気力線を定義しています。
電場は、$+1\:\mathrm{ [c\:]}$ の電荷が受ける力で示される。
電気力線は、正電荷を電場内においたときに、その正電荷が動く向きである。
のでした。
では電位とは何だったでしょうか?
電位とは・・・
その地点で $1\:\mathrm{ [c\:]}$ の電荷が持つ位置エネルギーを電位という
のでした。
もっと具体的に言うと、$1\:\mathrm{ [c\:]}$ の電荷を運ぶときに出入りする仕事やエネルギーのことです。
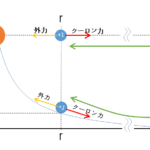
そこで、$1\:\mathrm{ [c\:]}$ の正電荷を次の図で下の極板から上の極板まで運ぶときの仕事を考えます。
(注:前の図と違って正に帯電した極板を上に持ってきています)

正電荷は電気力線方向に力を受けます(なぜかわかりますね?)から、その力に逆らって上の極板まで持ち上げるには外力による正の仕事が必要です。
したがってこの場合、上の極板は下の極板よりも高い電位を持つということになります。
つまり、
「電位の高い方から電位の低い方へ電気力線が向く・電場が向く」
「電気力線の矢印の向きに電位は下がる」
ということが一般的に言えます。

電場は電位の高い方から低い方へ向くのですね!
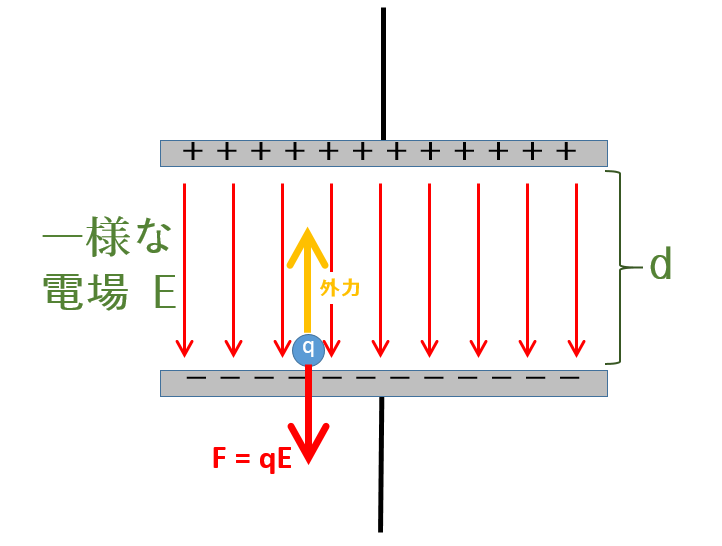
それでは今、図のように一様な電場 $E$ があるとき、極板間隔を $d$ としましょう。

このとき、$q$ の電荷を下の極板から上の極板まで運ぶ仕事 $W$ を考えます。
$q$ の電荷が電場から受ける力 $F$ は $F=qE$ と示されます。
一様な電場ですから、$E$ の大きさはどこでも同じです。
よって、そのときに外力がする仕事 $W$ は $W=Fx$ より、(力は釣り合っているため加える外力の大きさ $F$ も $qE$ でよい)
$W=Fx=(qE)\times d$
ここで、電極間の電位差を $V$ とすると、$W=qV$ であるから、
$W=Fx=(qE)\times d=qV$

$1\:[V\:]$ は $1\:\mathrm{ [c\:]}$ の電荷を
運ぶときに $1\:\mathrm{ [J\:]}$ の仕事を要するということです。
よって、電気量 $q$ の電荷を $V$ の電位差の間で
移動するときの仕事・エネルギーの出入りは $W=qV$
ということになります。
したがって、
$Ed=V$
となります。
電場の大きさは電位グラフの傾きである
さて、重要な事項をここで一つ考えます。
こういったイメージをしっかり持ってほしいと思います。
上の内容から、電場 $E$ が一様であるなら、$Ed=V$ ということがいえます。
つまり、
$E=\dfrac{V}{d}$
です。
したがって、電場 $E$ の単位は、$\mathrm{ [N/c\:]}$ のほかに $\mathrm{ [V/m\:]}$ ともかけます。
これは $E$ の大きさが $1\:\mathrm{ [m\:]}$ あたりの電位差であることを示しています。
電磁気では、電場の単位としては、この $\mathrm{ [V/m\:]}$ をおもに使います。

単位を換算して確かめてみましょう。
$W=qV$ より、$V=\dfrac{W}{q}$ よって $\mathrm{ [V\:]}=\mathrm{ \dfrac{[J\:]}{[c\:]}}$
ゆえに、
$\mathrm{ [V/m\:]}=\mathrm{ \left[\dfrac{J}{c}\cdot \dfrac{1}{m}\right]}$
ここで $W=Fx$ より $\mathrm{ [J\:]}=\mathrm{ [N \cdot m]}$ だから、
$\mathrm{ [V/m\:]}=\mathrm{ \left[\dfrac{J}{c}\cdot \dfrac{1}{m}\right]}=\mathrm{ \left[\dfrac{N\cdot m}{c}\cdot \dfrac{1}{m}\right]}=\mathrm{ [N/c\:]}$
これらの関係をグラフにしてみます。
一様な電場の場合、$E$ は一定ですから、次のようなグラフになるはずです。($E$ が一定なのでグラフは直線です)
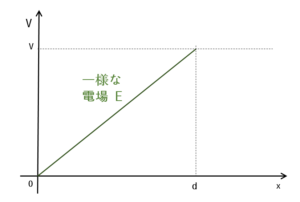
となると、$E=\dfrac{V}{d}$ とはこのグラフの傾きですね。
さらに拡張すると、一様でない電場の、次のような $V-x$ グラフにおいてもその傾きは電場を示していると言えます。
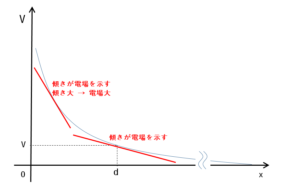
つまり、距離 $d$ が同じなら、電位差が大きいほど電場は大きい・強い、ということですね。
空間の電気的な歪が大きいというイメージです
問題を解く
問題をやってみましょう。
$x$ 軸に平行な電場があり、位置 $x$ と電位 $V$ の関係は次のグラフで示される。

(1) 図の A、B の点の電場の大きさを求めよ。
(2) 電気量 $1.0 \times 10^{-6}\:\mathrm{ [c\:]}$ の正電荷を点 $B$ から 点 $O$ まで静かに運ぶとき、外力のする仕事を求めよ。
(3) 電気量 $1.0 \times 10^{-6}\:\mathrm{ [c\:]}$ の正電荷を点 $B$ から 点 $O$ まで運ぶとき、静電気力のする仕事を求めよ。

答え
(1) 図の A、B の点の電場の大きさを求めよ。
A : グラフから一様な電場とわかります。
$E=\dfrac{V}{d}=\dfrac{12}{0.40}=30\:\mathrm{ [V/m]}$
B : グラフの傾きは 0 です。
$E=\dfrac{V}{d}=0\:\mathrm{ [V/m]}$
(2) 電気量 $1.0 \times 10^{-6}\:\mathrm{ [c\:]}$ の正電荷を点 $B$ から 点 $O$ まで静かに運ぶとき、外力のする仕事を求めよ。
電場が存在しないため BO 間では物体にかかる力は 0 です。
なので必要な外力も 0 です。
よって、BC 間は仕事は 0 です。

力が 0 なのにどうやって動かすのでしょうか?

ほぼ 0 とみなせるような力を一瞬だけ加えます。
そうすると、時間はかかっても慣性の法則により、
B から C まで移動するはずです。
このとき、ほぼ 0 の力だったので、仕事も 0 とみなせます。
残るのは CO 間の仕事ですがこの場合、電位が高いのは C の方です。( C が 12 V で O が 0V )
したがって、電気力線は C から O へ向かいます。
いま問題となっているのは正電荷ですから、電荷は C から O へ向かう力を電場から受けます。(注:電荷が負のときは逆です)
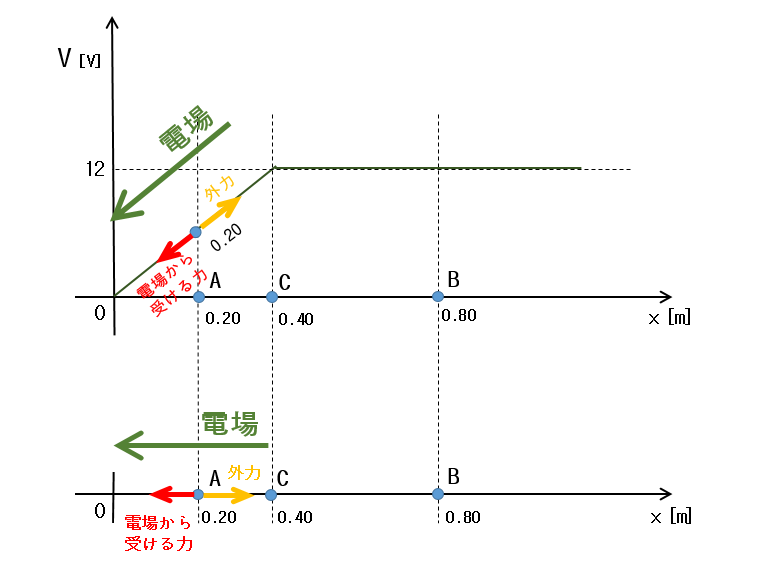
よって外力は O から C へ向かう力をかける必要があります。
この外力をかけながら、電荷を C から O へとゆっくりと移動させます。
そのため、この外力のする仕事は負となります。
ゆえに、
$W=qV= -1.0 \times 10^{-6}\:\mathrm{ [c\:]} \times 12\:\mathrm{ [V\:]} $
$~~~=-1.2 \times 10^{-5} \:\mathrm{ [\:J\:]}$
となります。
仕事ですから、$W=Fx$ で考えても当然同じになります。$F=qE$
$W=Fx=qEd=qV$
(3) 電気量 $1.0 \times 10^{-6}\:\mathrm{ [c\:]}$ の正電荷を点 $B$ から 点 $O$ まで運ぶとき、静電気力のする仕事を求めよ。
(2) と同様に考えます。電荷の電気量は (2) と同じです。
このとき、静電気力のする仕事は正です。
よって、(2) の符号を変えてやればいいことになります。
つまり、
$W=+1.2 \times 10^{-5} \:\mathrm{ [\:J\:]}$

もしも、仕事の正負などで悩むことがあればそれはチャンスです!
この機会に、悩んだ箇所や分野をもう一度振り返って完璧にしてしまいましょう!
まとめ
さて今回のまとめです。
- 電場は電位の高い方から低い方へ向く
- 電気力線の矢印の向きに電位は下がる
- $E=\dfrac{V}{d}$ ただし一様な電場 $E$ であることに注意
- $V-x$ グラフにおけるグラフの傾きはその点での電場の大きさを示している
- 距離が同じでも電位差が大きいところほど電場は大きい・強い
したがって空間は電気的に大きく歪んでいる
繰り返しになりますが、こういった基礎の事柄をどれだけ正確に理解しているかでその後の勉強の成否がわかれます。
知らない語句は必ず調べて、理解しておきましょう。
次回は、導体内・不導体内の電場と電位、そしてそのグラフ解説の予定です。
動画でも解説予定です。そのうちに・・・スタディサプリもおすすめですよ。
Z会Asteria まずは無料でお試しください
![]()




































コメント