電磁気は力学とともに入試で非常に良く出る分野です。
十二分に対策をしましょう。
右手の法則や右ねじの法則、フレミングの左手則、レンツの規則などいろいろな法則や式が登場しますが、電磁気分野については、ある程度「公式」を覚えるという作業が必要になることは事実です。
というのも、導出過程が複雑難解であるため、導出に時間がかかってしまうことにあります。
特に試験のときなど、単振動であればちょいちょいと式を導出できるのですが、電磁気分野はなかなかそういうわけには行かないのです。
直流電流の作る磁場
エルステッド(デンマーク 1777-1851)は直線電流の周囲で磁石の磁針が振れること見出しました。
つまり、電流はその周囲に磁場を作る ことの大発見でした。
別個の現象だと考えられていた、電流と磁場は互いに関連しあうということが明らかになったのです。
直流電流が作る磁場ですが、高校物理では、大きく分けて以下の3つの場合があります。
- 直線電流
- 円形電流
- ソレノイド
ですね。それでは順番に見ていきましょう。
アンペールの法則による式の導出は以下で!
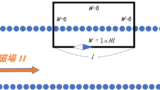
直線電流による磁場
十分に長い導線があるとします。
その導線を流れる電流 $I$ が周囲に作る磁場は次の図のようになっていることが知られています。
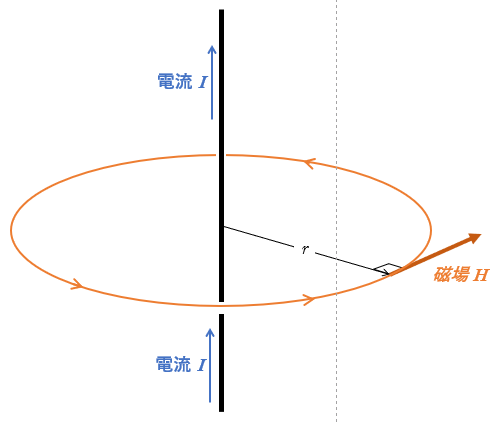
このとき、導線から距離 $r$ の位置で、電流が作る磁場の大きさ $H$ は、
$H=\dfrac{I}{2\pi r}$
で示されます。

また磁場の向きは、「右ねじの法則」「右手の法則」により定義されています。
- 右ねじの法則
右ねじの進む向きに電流を流したとき、磁場の向きは右ねじの回る向きになる - 右手の法則
右手で「いいね」を作る。親指の向きに電流を流すと、他の指の方向に磁場が生じる
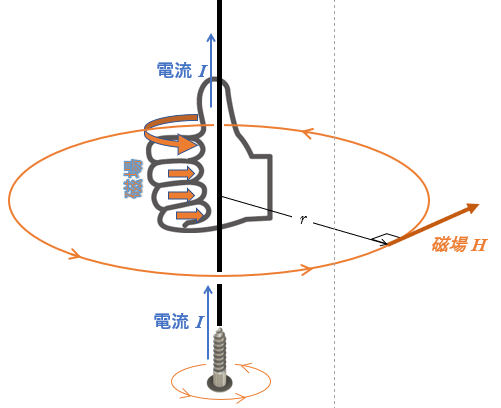

個人的には、右ねじより右手の法則のほうが
間違いにくいと思っています。
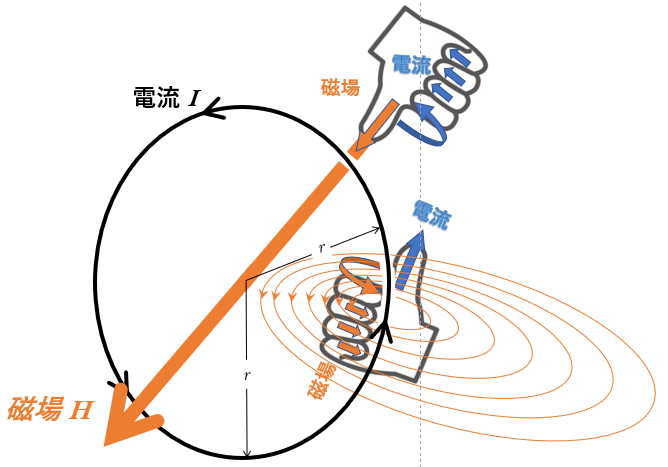
円形電流
$N$ 巻きの円形導線に流れる電流 $I$ が、その円の中心に作る磁場の大きさ $H$ は、
$H=N\dfrac{I}{2r}$
で示されます。
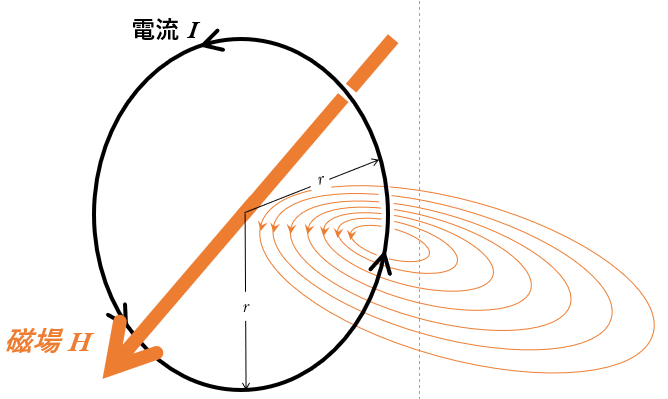
磁場の向きは、右手の法則を使った考えましょう。

注意
よく間違えるのが、直電流の作る磁場の式と、円形電流の作る磁場の式を取り違えてしまうことです。
そうすると、その後の問題が全滅するという悲劇が待っています。
次のように覚えると間違いが少なくなります。
線に $\pi$ あり、円に $\pi$ 無し
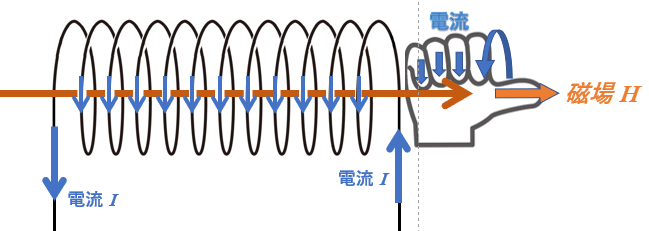
ソレノイド
ソレノイドは図のように、十分に長い円筒に導線を密に巻いたものです。
導線に電流 $I$ を流すとき、ソレノイド内部に作る磁場は、ソレノイド内部であればどこでも同じです。そして、その大きさは、
$H=nI$
と表されます。
$n$ は導線の単位長さ当たりの巻き数です。(つまり、$1\:m$ あたりの導線の巻き数)
磁場の方向は、右手の法則を使えば簡単です。
ソレノイドの磁場の式はアンペールの法則を使えば簡単に導出できます。

動画
ちょっと古いですが、動画で解説しています。
まとめ
- 直線電流による磁場 $H=\dfrac{I}{2\pi r}$
- 円形電流による磁場 $H=N\dfrac{I}{2r}$
- ソレノイドによる磁場 $H=nI$
電流が磁場から受ける力にについてはこちらの記事を
その他、アンペールの法則・ビオサバールの法則等は別記事で。
アンペールの法則についての記事は以下になります。





































コメント