相互誘導について解説しています。
また、勘違いしやすい電位問題についても扱っています。
相互誘導
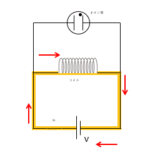
図でコイル 1 のスイッチを開閉すると、コイル 1 を流れる電流が変化し、コイル 1 の作る磁場が変化する。
そのため、コイル 2 を貫く磁場が変化し、ファラデー電磁誘導の法則に従って、コイル 2 に誘導起電力が生じる。
この現象を相互誘導と呼びます。
このとき、コイル 1 とコイル 2 は直接接続されておらず、空間を隔ててエネルギーを伝えることができます。
ICチップの埋め込まれたカード、電動歯ブラシやスマホのワイヤレス充電などにも使われています。
また、IH(Induction Heating)は相互誘導の一種の渦電流を利用しています。
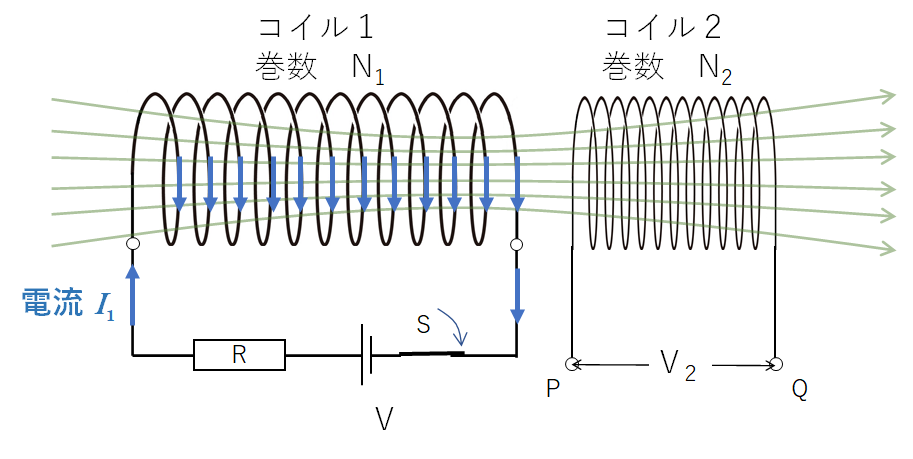
コイル 2 に生じる誘導起電力 $V_2$ は、コイル 2 を貫く磁束 $\Phi_2$ 、コイル 2 の巻き数 $N_2$ 、時間 $t$ として次式で示されます。
$V_2=-N_2\dfrac{\Delta \Phi_2}{\Delta t}$
ここで、コイル 2 を貫く磁束 $\Phi_2$ はコイル 1 が作った磁束そのものですから、ここでコイル 1 についてもう一度おさらいしましょう。別の記事、自己誘導を参照してください。
コイル 1 において、
- コイル 1 の長さ $l$
- コイル 1 の単位長さ当たりの巻数 $n_1$
- 電流 $I_1$ が作る内部磁場の強さ $H_1=n_1I_1$
- 磁束密度 $B_1=\mu_1 H_1= \mu_1 n_1I_1$ ( 透磁率 $\mu_1$ )
- 磁束 $\Phi_1=B_1S_1=(\mu_1 H_1)S_1=(\mu_1 n_1I_1)S_1$
とした場合、微小変化 $\Delta$ を考えると、
$\Delta\Phi_1=\Delta(B_1S_1)$
$~~~~~~=\Delta(\mu_1 n_1S_1 I_1)\qquad \qquad\qquad \mu_1 n_1S_1 $ は一定のため、
$~~~~~~=\mu_1 n_1S_1\Delta I_1$となります。
ここで、コイル 1 を貫く磁束線の変化がコイル 2 を貫くので、コイル 2 を貫く磁束の変化 $\Delta \Phi_2$ は $\Delta \Phi_1$ に比例します。
したがって、比例定数を $k$ とすると、
$\Delta\Phi_2=k\Delta \Phi_1$ ここで$\Delta \Phi_1=\mu_1 n_1S_1\Delta I_1$ でしたから、
$\Delta\Phi_2=k(\mu_1 n_1S_1\Delta I_1)$ $k_2=k\mu_1 n_1S_1$ とおくと、
$\Delta\Phi_2=k_2\Delta I_1$
とすることができます。
ファラデー電磁誘導の法則よりコイル 2 に生じる誘導起電力 $V_2$ は
$V_2=-N_2\dfrac{\Delta \Phi_2}{\Delta t}$ $\Delta\Phi_2=k_2\Delta I_1$ より
$~~~~=-N_2k_2\dfrac{\Delta I_1}{\Delta t}$ $M=N_2k_2$ とおくと、
$V_2=-M\dfrac{\Delta I_1}{\Delta t}$
まとめ
相互誘導の誘導起電力 $V_2$
$V_2=-M\dfrac{\Delta I_1}{\Delta t}$
$V_2$:コイル 2 に生じる誘導起電力 $M$:相互インダクタンス $I_1$:コイル 1 を流れる電流 $t$:時間
$M$ の単位には自己誘導と同じく H(ヘンリー)を用いる。
電位についての問題
次の問題をしてみましょう。
間違いやすい箇所を選んでみました。
問題
次の図を見てください。
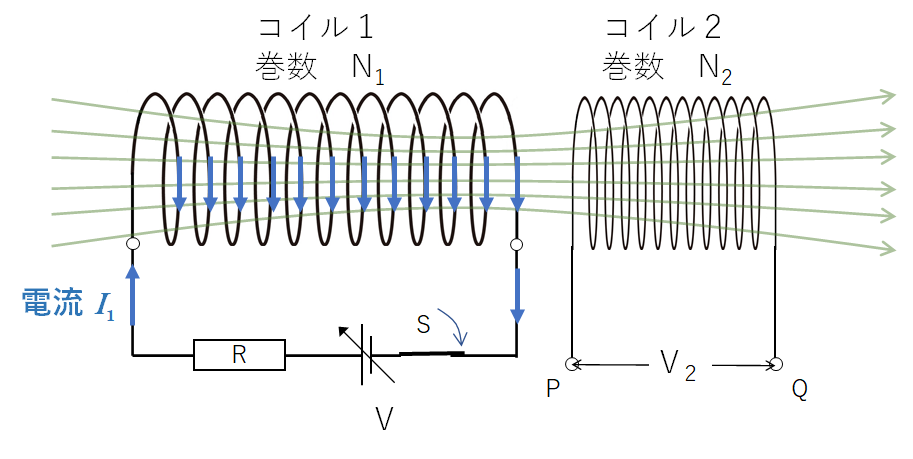
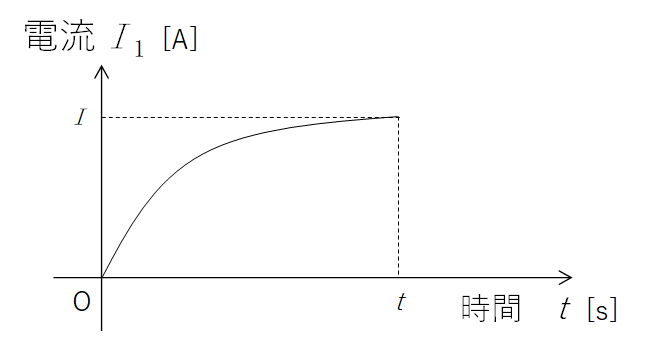
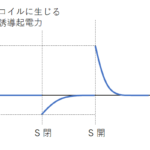
このとき、次のグラフのようにコイル 1 を流れる電流 $I_1$ が変化したとします。
コイル 2 の P と Q では、電位が高いのはどちらでしょうか?

答え
P
グラフより、コイル 1 を流れる電流が時間 $t$ で $I$ 増加。
それにより、コイル 1 を貫く磁束が増加するため、コイル 2 を貫く磁束も増加していきます。

このときレンツの法則によりコイル 2 にはこの磁束の変化(増加)を打ち消すような向き・・・図の左向きの磁束ができるように誘導起電力が生じます。
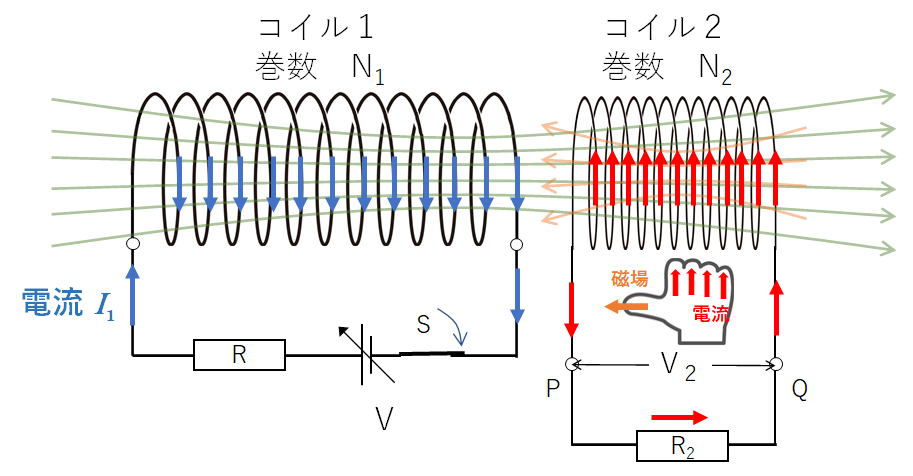
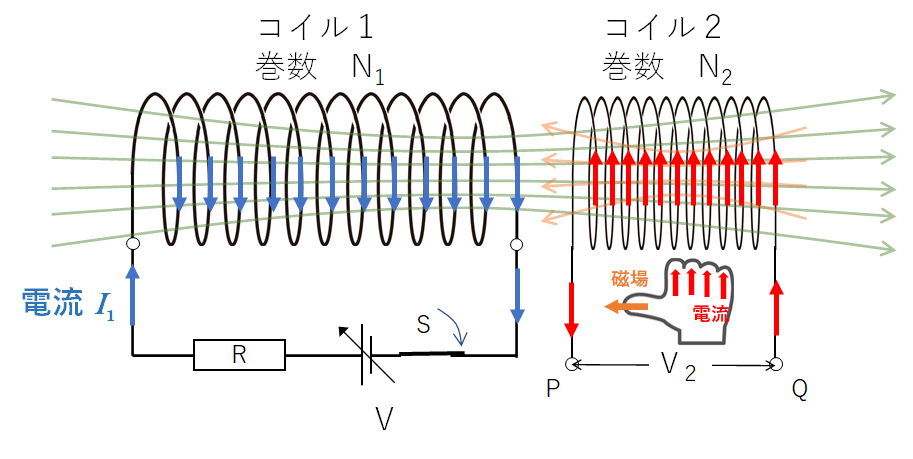
右手の法則でコイル 2 を親指が左を向くようにつかむと、コイル 2 に生じる誘導電流の向きは、コイル 2 の内部を Q から P へ向かいます(下図)。
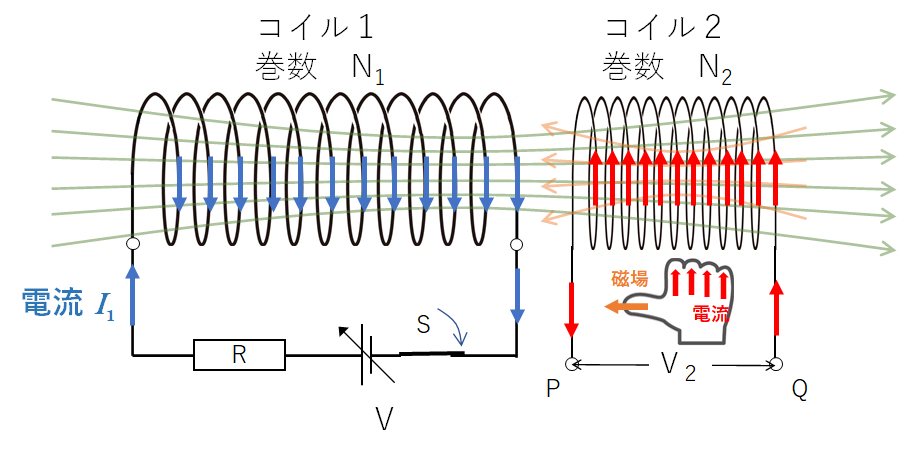
ここで一般に言われる、「電位の高いほうから電位の低いほうへ電流が流れる」ということから、Q のほうが P よりも電位が高いと勘違いしないように気を付けなくてはなりません。
なぜ P 端の電位が高いのでしょうか?
ここで、P Q 端に抵抗をつないでみます。
抵抗では P から Q へ向けて自然に電流が流れています(下図)から、電位が高いのは P ということになるのです。
ただし、コイル 2 の内部では電位の低いほうから高いほうへ電流が流れます。

コイル 2 内はローレンツ力を受けて電子が強制的に運動させられているということです。
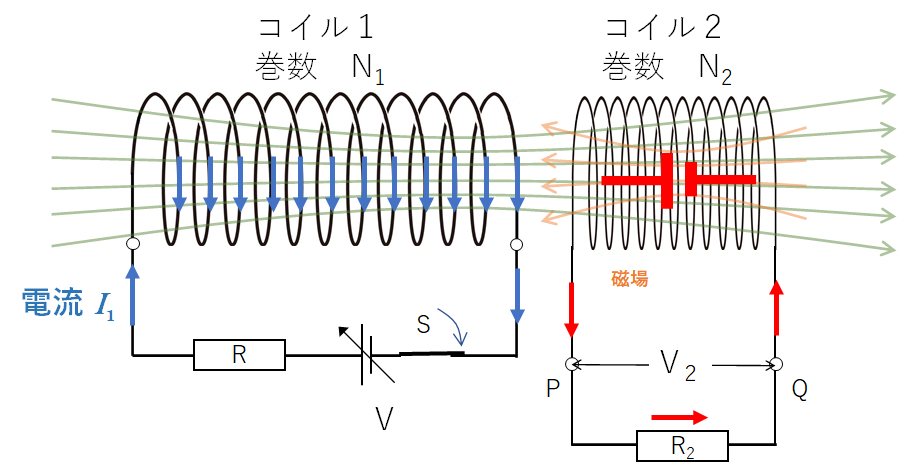
同じように、電池の内部でも電位の低いほうから高いほうへ電流が流れていますね。
つまり、コイル 2 は図のような電池とみなして考えればよいことになります。





































コメント