ニュートンリング
ニュートンリングとは
ニュートンリングは次のようなものです。

図は真横からの断面図です。
平面ガラスと平凸レンズ(片面が平ら、片面が球面)を用います。
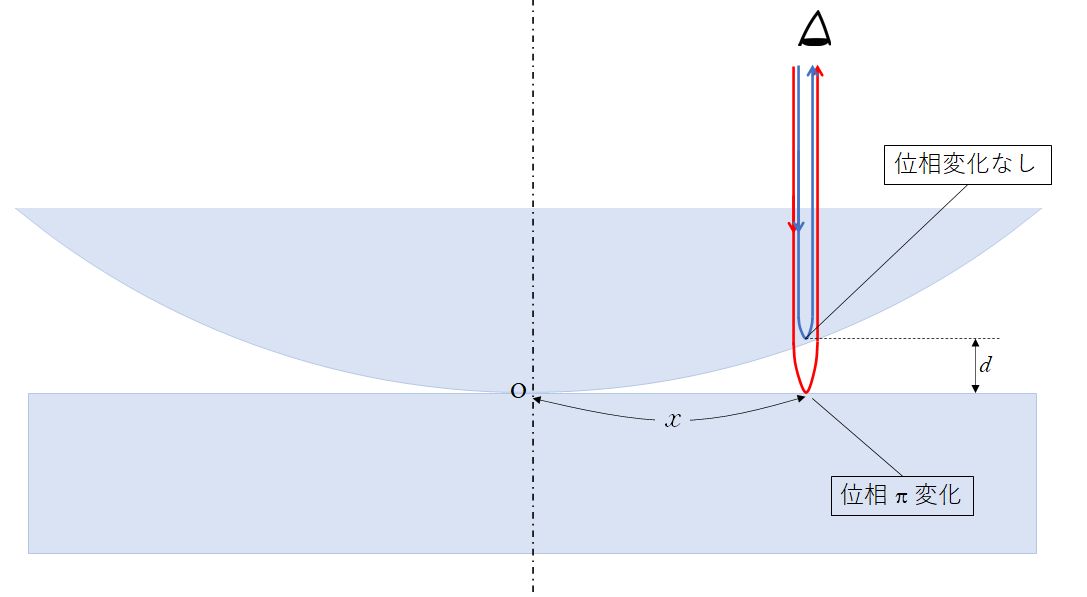
これに上から単色光をあてると、同心円状の明暗の干渉縞を観察することができます。

特徴としては、中心部は暗部、外へ向かうにつれ徐々に干渉縞の間隔が短くなっていくことです。
ニュートンリングの経路差
レンズの半径を $R$ 、中心 O から $x$ だけ離れたところの空気層の厚みを $d$ とします。
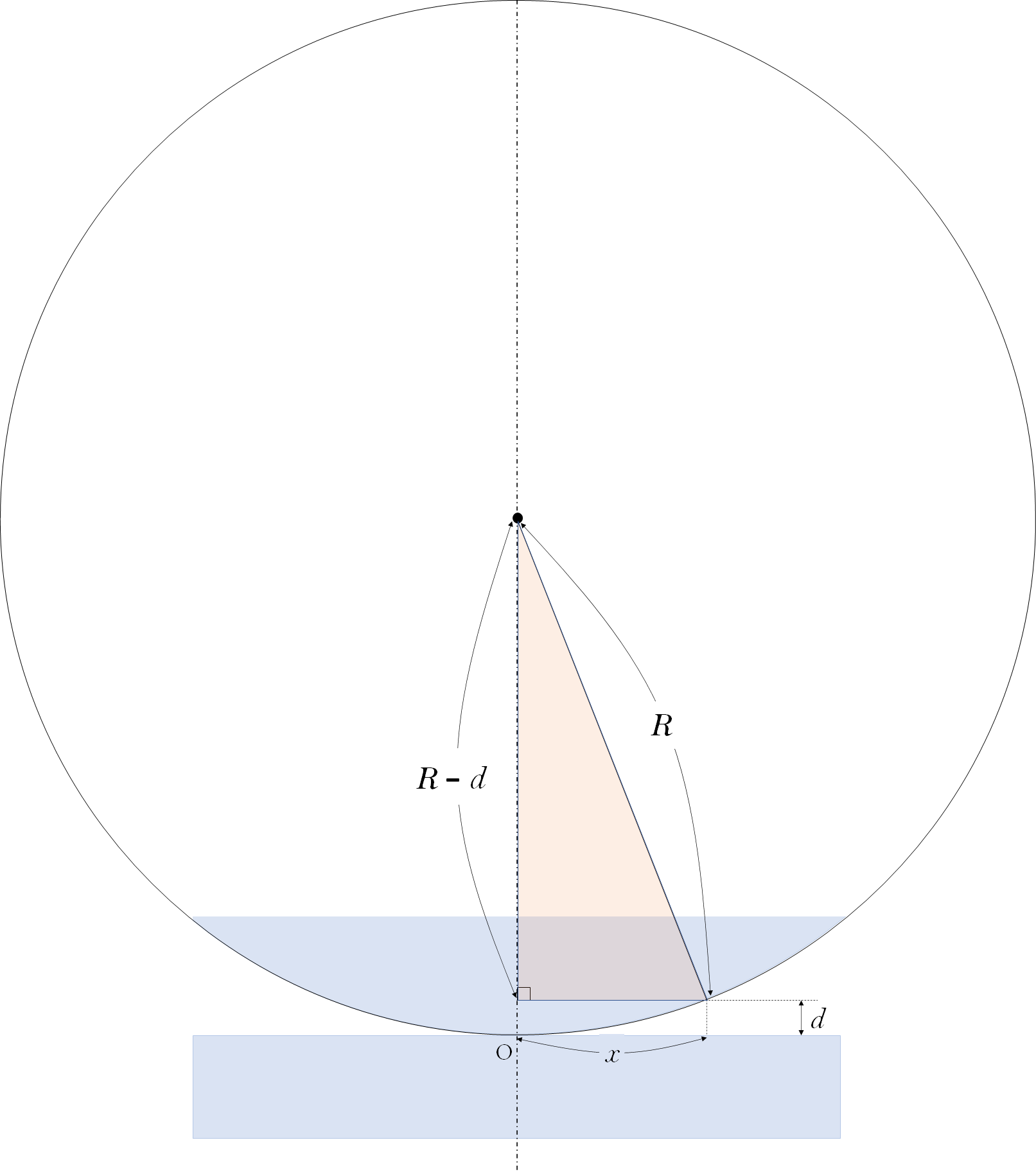
そうすると、図のオレンジの直角三角形を考えて、三平方の定理より、
$R^2 = (R-d)^2+x^2$
$R^2 = R^2 -2Rd + d\,^2 + x^2$
ここで、 $d\,^2 \fallingdotseq 0 $ とすると、( $R \gg d $ )
$2Rd = x^2$
$2d = \dfrac{x^2}{R}$
平面ガラス上面で反射する際に、位相が $\pi$ 変化しますから、ヤングの実験で示した基本的な式の明暗条件が入れ替わります。(注意:レンズとガラスの間に液体を注入するなど、条件により変わってきますから都度確認してください。)

反射の際の位相変化は
屈折率小 ⇒ 屈折率大 へ行こうとして反射・・・位相 $\pi$ 変化
屈折率大 ⇒ 屈折率小 へ行こうとして反射・・・位相変化なし
したがって、
暗線 : $2d = \dfrac{x^2}{R} = m \lambda$
明線 : $2d = \dfrac{x^2}{R} = m \lambda + \dfrac{1}{2}\lambda$
$m=0,\:1,\:2,\:3,\:\cdots\cdots$
となります。

波動の干渉問題についてはいろいろとバリエーションがあるのですが、その核心はすべて同じです。
物理とは、すべての現象を説明できるマスターキーを探している・・・ようなイメージです。
すなわち、波動であるなら、音、光などを問わず同じ理論で理解できる・・・ようにしよう! というわけです。
くさび型空気層とニュートンリング
くさび型空気層の光の干渉と違うところは、
- くさび型空気層では明暗の干渉縞が平行・等間隔に並ぶ
- ニュートンリングでは干渉縞が同心円状で、その間隔が外側に行くにつれ狭くなる
という点です。
これはなぜでしょうか?
それは断面を見れば明らかです。
くさび型空気層の装置の断面図を見ると、空気層が三角形をしていることがわかります。
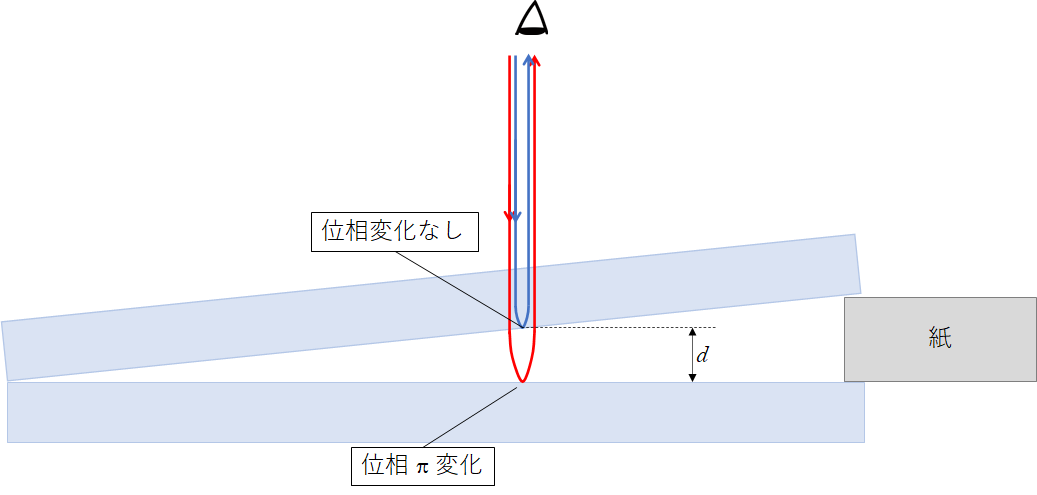
ニュートンリングの場合の断面図を見ると、凸レンズを使用しているため、空気層が三角形にはならず上面はカーブを描いています。

この違いにより、干渉縞の間隔がくさび型空気層とニュートンリングでは違ってくるのです。
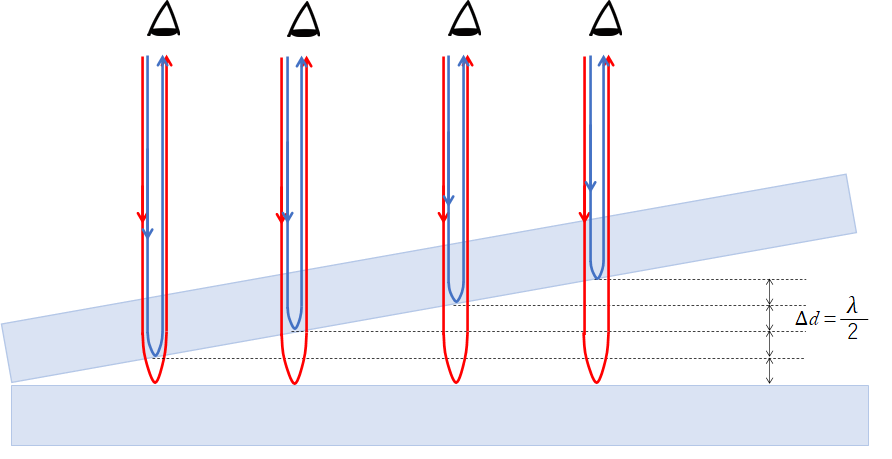
下の図で、隣り合う暗線(明線)同士の長さの差は一定で、 $\lambda$ の長さの光が入る必要があります。(よって、図の $\Delta d = \dfrac{\lambda}{2}$) くわしくはここ
しかし、球面なので外側に行くつれ少しの距離でこの 条件を満たすことになります。
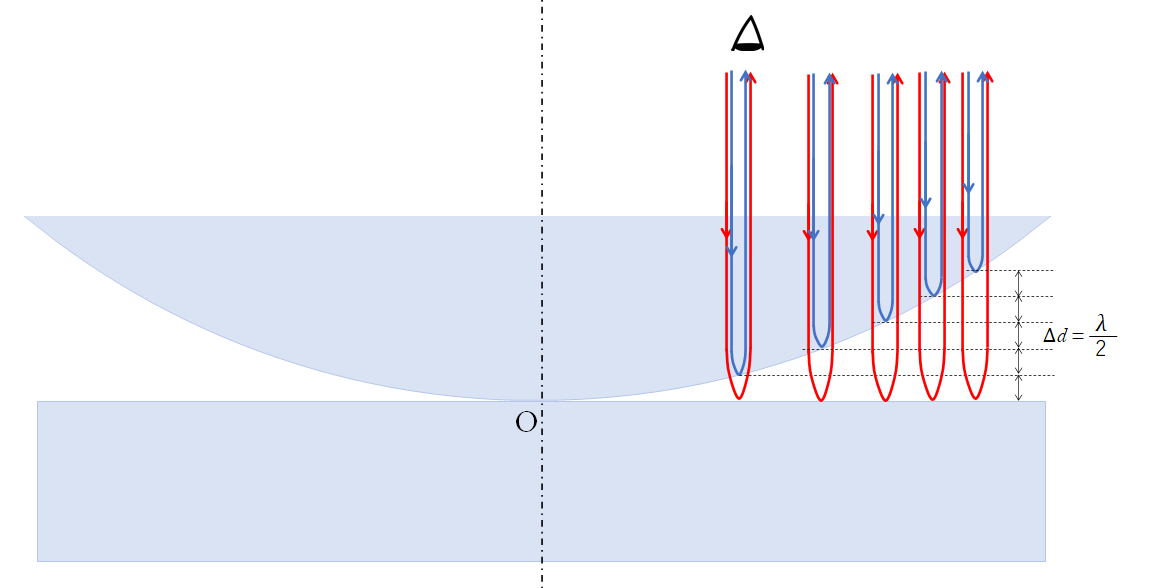
くさび型空気層の場合は直線なので等間隔になるのです。
ニュートンリングの中心部の明暗
通常の(空気層の場合)ニュートンリングの中心では暗線になります。
これはくさび型空気層で説明したのと同じ理屈です。
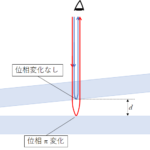
すなわち、中心では空気層がほぼ 0 となり、ガラス平面上部で反射した光は位相が $\pi$ 変化しますが、レンズの下部で反射する光の位相変化がないことで説明できます。

またニュートンリングでは中心部に行くつれ、空気層が非常に薄くなるため中心部の黒の部分は大きく見えます。
ニュートンリングを下から見ると
同様の問題をくさび型空気層で扱っています。

全く同じ理屈で、下から見ると明暗が逆転して見えるはずです。

そもそも、もし上から見ても下から見ても明るく見えるならば、装置を工夫すれば光を無限大に増幅できることになり、おかしいですね。




































コメント