物理のエッセンスの電磁気編コンデンサーの36番について解説します。
コンデンサーのエネルギーの問題ですが、基本的な考え方は力学的なエネルギーの問題と変わるところはありません。
世の中のエネルギーは形を変えて保存されていくわけですから。
動画
物理のエッセンスの電磁気編コンデンサーの36番についてYouTube動画解説しています。
問題について
物理のエッセンスの電磁気編 コンデンサーの問題 36* について解説しています。
64ページの問題を見てください。
最初に電圧 $V$ で充電しておいたコンデンサーと、充電していないコンデンサーとを抵抗を介して接続します。
そして、コンデンサーの電荷移動が終わったときまでの抵抗の発熱分を求めよ、という問題になります。
コンデンサーのエネルギー
コンデンサーのエネルギー $E$ の式は
$E=\dfrac{1}{2}QV$
ですが、$Q=CV$ を用いて変形することで3つの式を得ることができます。
\begin{eqnarray}
E&=&\dfrac{1}{2}QV\\\\
&=&\dfrac{1}{2}CV^2\\\\
&=&\dfrac{Q^2}{2C}\\\\
\end{eqnarray}
エネルギーの原理

この問題は電磁気の問題ですが、エネルギーに関しての考え方は力学的なものと同じです。
⇒ エネルギーは熱力学第一法則により形を変えて保存することになっています。
エネルギーの原理をもう一度考えてみましょう。
最初のエネルギーを $E_0$ とし、最後のエネルギーを $E$ とします。
そうすると、 仕事を $W$ 、あるいはエネルギーの差分を $\Delta E$ としてやると次の式が成り立ちます。
$E_0+W=E$
$E_0+\Delta E=E$
これはエネルギーを考える上で非常に重要です。
よく引き算で書かれているものを見ますが、足し算のほうが直感的にわかりやすいのではないかと思います。
みなさんもエネルギーの考え方に関しては足し算にすることをおすすめします。
ジュール熱

それでは、エネルギーの原理を使って考えてみましょう。
先程見てきたように、$E_0+\Delta E=E$ ですね。
ここで $\Delta E$ がジュール熱に変わると考えていいでしょう。
では計算してみましょう。
コンデンサー $C_1$ は最初 $V$ で充電されていたので、そのエネルギーは $\dfrac{1}{2}C_1V^2$ とかけます。コンデンサー $C_2$ は充電されていないので、そのエネルギーは $0$ ですね。
したがって、
$E_0=\dfrac{1}{2}CV^2$
そして、コンデンサーを接続したあとのエネルギー $E$ は、
$E=\dfrac{Q^2}{2C}$
を使って考えます。
またこの回路は並列回路です。そして、コンデンサーが並列につながっているとき、その合成容量は単純に各コンデンサーの容量を足すだけです。
したがって、この問題の場合、各コンデンサーの容量は $C_1$ と $C_2$ なので、合成容量は $C_1+C_2$ となります。
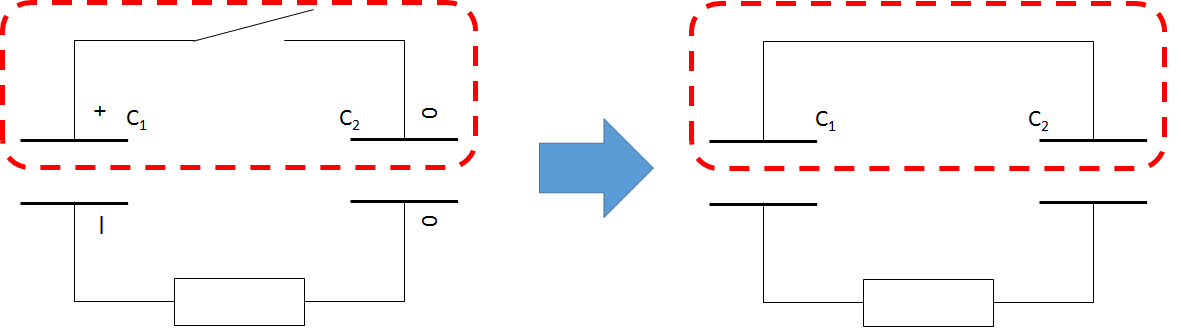
そしてこの場合、コンデンサーの電気量は増減しません!
図の赤枠の中の電気量はスイッチを入れても、$Q_1+Q_2=C_1 V$ のままです。
そうすると、エネルギーの原理の式から
\begin{eqnarray}
E_0+\Delta E&=&E\\\\
\Delta E&=&E-E_0\\\\
\Delta E &=&\dfrac{(C_1V)^2}{2(C_1+C_2)}-\dfrac{1}{2}CV^2\\\\
\Delta E &=&-\dfrac{C_1C_2V^2}{2(C_1+C_2)}\\
\end{eqnarray}
この場合は値に $-$ がついています。
よって、$\Delta E$ のエネルギーの損失があったわけです。
それがすべてジュール熱になったと考えます。
問題は発熱量 $H$ ですから、
$H=\dfrac{C_1C_2V^2}{2(C_1+C_2)}$
となります。
YouTube koko物理 物理解説チャンネル





































コメント